キーワード

• Landau関数

• 熱力学関数

• 凸性

• Legendre変換

• 相分離

• 化学ポテンシャル

該当箇所

磁場項を除いたLandau関数を

$$
\tilde{g}(T,m)=f_0+Am^2+Bm^4
$$

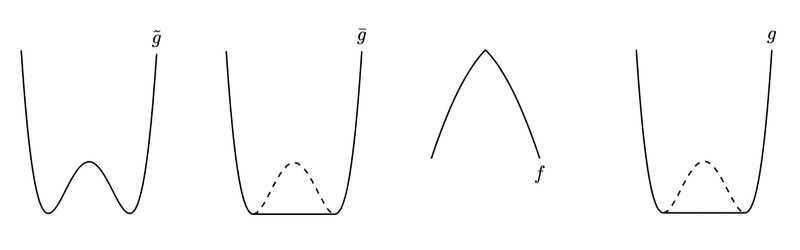
とおいたとき、（中略）$${\tilde{g}(T,m)}$$はGibbsの自由エネルギーに対応しているようにみえる。Helmholtzの自由エネルギーが磁場$${h}$$に関して上に凸の関数であることに対応して、Gibbsの自由エネルギーは磁化$${m}$$に関して下に凸の関数であることが、熱力学的に要請される。しかしながら、図4.1右のように$${\tilde{g}(T,m)}$$は下に凸でないときもあるから、$${\tilde{g}(T,m)}$$とGibbsの自由エネルギーを同一視することはできない。

（中略）

そこで図4.2のように点線の部分を直線に置き換える。このようにすると$${h}$$と$${m}$$は$${h=0}$$を除いて１対１となり、自由エネルギーは下に凸の関数となる。直線より上を通るとすると下に凸の性質が成り立たなくなってしまうし、下を通るわけにもいかないので、直線になるしかない。（中略）修正された$${\tilde{g}(T,m)}$$から得られた自由エネルギー$${f(T,h)}$$を逆Legendre変換すると、下に凸の性質を持つ正しいGibbsの自由エネルギーを得ることができる。

疑問点

• $${\tilde{g}(T,m)}$$の修正方法は妥当か

• 修正後の$${\tilde{g}(T,m)}$$は$${f(T,h)}$$の逆Legendre変換 (Gibbsの自由エネルギー) と同じものか

解説

特に$${\tilde{g}(T,m)}$$が指すものが複数あるので、以下では

1. 低温相で凸性を破るLandau関数$${\tilde{g}(T,m)}$$

2. $${\tilde{g}(T,m)}$$を適切に修正することで得られる凸関数$${\bar{g}(T,m)}$$

3. $${\bar{g}(T,m)}$$から得られるHelmholtzの自由エネルギー$${f(T,h)}$$を逆Legendre変換した$${g(T,m)}$$

とする。

Landau関数の修正法の妥当性

$${\tilde{g}}$$のグラフ上の2点をつなぐ操作自体はp. 78の相分離で正当化される。しかしグラフ上のどの2点を結ぶかという問題は残っている。

化学ポテンシャルがある場合、すなわち数保存が成り立つ場合、相分離後は$${∂\tilde{g}/∂n=\mu}$$が2相で共通する点を結ぶことになる。今の場合、各状態を取る粒子密度$${n}$$は磁化$${m\propto n_\uparrow-n_\downarrow}$$と同一視できるので、相分離を起こす場合は$${\bar{g}}$$として共通接線が実現される。従って$${\bar{g}}$$は$${C^1}$$級であることは保証されるが一般に$${C^2}$$級ではない。また特に$${\mathrm{Z}_2}$$対称性を破った場合、相分離によって現れる2つの状態は$${\tilde{g}}$$を最小とする解ではない。

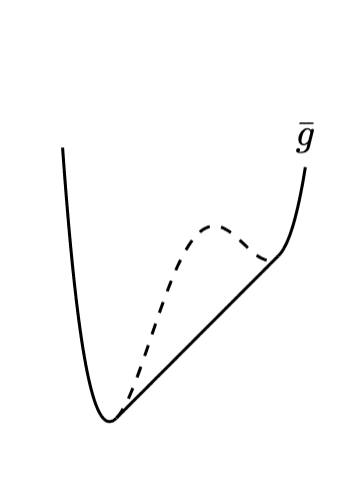
化学ポテンシャルが0の場合、すなわち保存量が存在しないとき、相分離後に混ざる状態には特別な制限がつかないと考える。自由エネルギーをそれぞれの状態近傍で下げることで、極小値どうしの混合になるだろう。Z2対称性を破る場合、実現される$${\bar{g}}$$は一般に解析性がクソ悪く、$${C^1}$$級ですらない。また凸性すら破れる。

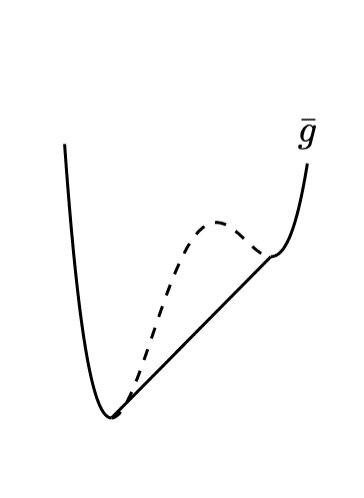
普通Isingスピンは粒子数が増減することを考えないので、共通接線が実現される。

修正されたLandau関数とGibbsの自由エネルギーの等価性

$${\bar{g}}$$は化学ポテンシャルがある場合の共通接線から構成したとする。Gibbsの自由エネルギーはそもそもHelmholtzの自由エネルギーのLegendre変換として定義されるので、テキストの通りGibbsの自由エネルギーとして$${g}$$を使うのは妥当である。

とはいえ$${\bar{g}}$$が凸関数なので$${\bar{g}}$$と$${g}$$は一致する。直観的な説明は以下の通りである。$${\tilde{g}}$$の共通接線の接点より僅かに外側から関数形を膨らませることで、下図のように$${C^1}$$級の強凸関数$${g'(T,m)}$$を構成できるだろう。$${g'-mh}$$のうち$${\bar{g}-mh}$$と一致しない領域$${D}$$がLegendre変換に効くのは、$${D}$$のどこかで最小を取るときなので、最小点がより外側になる大きい$${h}$$では$${\bar{g}, g'}$$それぞれの変換で違いはない。$${g'}$$は強凸関数なので、Legendre変換した後逆Legendre変換すれば問答無用で$${g'}$$に戻る。$${D}$$の両端を狭めて共通接線に近づける極限をとれば$${g'\to\bar{g}}$$となる。

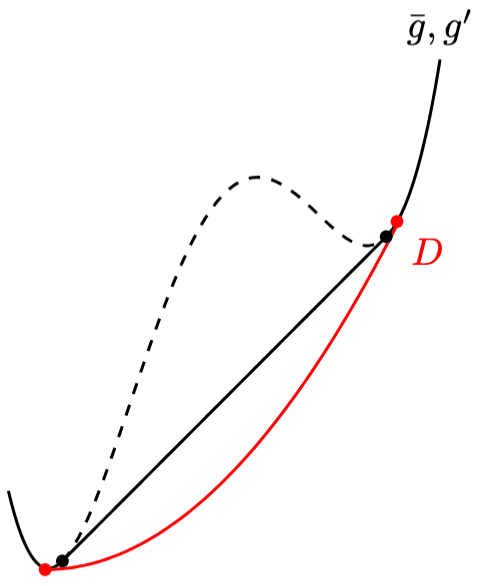
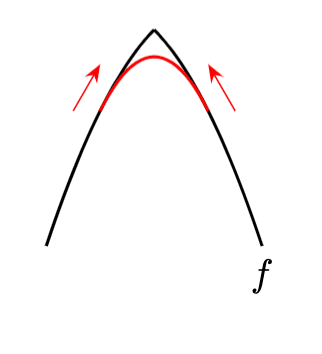
なお$${\bar{g}, g'}$$のLegendre変換がそれぞれ下図の黒線、赤線のようになることからも妥当性がわかる。