皆さん突然ですが、整数環を作ってみたくありませんか？
自然数の集合の次に現れる自分の指で数えられない数字を扱う第一歩となるものですね。

整数の集合、つまり自然数の集合$${\mathbb{N}}$$にそれらの’マイナスver.の数'を追加した集合を考えることで、$${\mathbb{N}}$$上ではできなかった「引き算」を考えることができるようになり、とても便利なものになりますね。

ただ、その　’マイナスver.の数'　ってなんやねん！って怒られないように、ちゃんと数学的に構成していきましょう。

自然数についての性質に関しては既知として使わせてもらいますね。
あとは同値関係も使います。これは一言で言うと、
「特定の条件のもとで集合の要素と要素を同一視し、同じものとして扱う」ためのものです。
一応同値関係に関する記事も書いてるので、良かったら読んでみてください。

整数の集合ℤの構成

$${\mathbb{N}^2=\mathbb{N} \times \mathbb{N}}$$上の同値関係$${\sim}$$を次で定める；

$${(n, m) \in \mathbb{N}^2, (n', m') \in \mathbb{N}^2}$$に対し
$${(n, m) \sim (n', m') :\Longleftrightarrow n + m' = n' + m}$$

この関係がちゃんと同値関係であることを証明する前に、
整数環を作るときのなんとなくの気持ちを説明しておきましょう。

冒頭で話した通り、整数環を作りたい理由は「引き算がしたい」
でした。
自然数の集合$${\mathbb{N}}$$では、"2-3"など、引き算の意味を考えると自然数の中には答えがなさそうですよね。
引き算ができるためには、最低限自然数n, mに対し'n-m'に対応するものが集合の中に存在しないといけません。
では、なかなかの脳筋プレイですが、形式的に'n-m'というものを集めた集合を考えたらどうでしょうか？そこには　'2-3'　や　'6 -2'　などがすべて含まれていて、少なくとも上で言った必要最低限の条件が満たされていることがわかりますね。

なので、この形式的な引き算の集まりを作れればいいわけですが、それは自然数の直積$${\mathbb{N}^2}$$によって達成されます。
つまり、$${(n, m) \in \mathbb{N}^2}$$に対して、
$${(n, m)}$$を"$${n - m}$$"と心の中で思えばいいわけですね。

ここで、$${(5, 3)}$$と$${(9, 7)}$$という$${\mathbb{N}^2}$$の二つの要素を見比べてみましょう。
この二つの要素は、気持ち的にはそれぞれ"5-3", "9-7"だと思うわけですよね。
どうでしょう。この二つを同じものとして扱いたくないですか？
僕たちがなんとなく知っている引き算の概念と照らし合わせれば、5-3と9-7は同じものになるはずですが、今は$${\mathbb{N}^2}$$で考えているのでこれらは別物扱いになってしまうんですよね。これは困りますね。
しかし、本来別物であるものを「同じ」と見做すことができればいいわけですから、同値関係を使えば簡単にクリアできそうです。

今、自然数の組$${(n, m)}$$と$${(n', m')}$$に対して、どういったときに同じと見做したいかを考えてみましょう。
二つの要素はそれぞれ n-m ,  n'-m' と思っているわけですから、この二つが
同じ値になるときに「同じ」と言いたいですよね。しかし、今の段階では引き算はあくまで心の中で思っているだけの形式的なもので、数学上ではまだ定義されていませんから、安直に $${n-m= n'-m'}$$ と書いてもそれは意味を持ちません。しかし、引き算が定義されたと思い込みながら式変形をしてみると、mとm'を入れ替えることで、同値（になるであろう）条件として
$${n+m'= n'+m}$$が得られます。自然数の足し算はすでに定義されたあとですから、この等式にはちゃんと意味を持たせられますね。
ということで、$${(n, m), (n', m')}$$が同一視される条件として、$${n+m'= n'+m}$$を導入すれば、なんかうまくいきそうですよね。
なので、$${\mathbb{N}^2}$$を上の条件によって同一視を入れたものを整数の集合$${\mathbb{Z}}$$としたわけです。

もちろん、このように定義したからといって、$${\mathbb{Z}}$$上で、自分たちが知っているような性質をすべて満たすような足し算、引き算、掛け算をちゃんと作れることは自明に示せるとかはありませんが、ちゃんとこれらを定義して整数環を作れます。

~は同値関係

上の定義による関係が同値関係になることを確認しましょう。

①$${{}^\forall (n, m) \in \mathbb{N}^2, (n,m) \sim (n, m)}$$

   明らかですね。n+m=n+mです。

②$${{}^\forall (n, m), (n', m') \in \mathbb{N}^2, [(n,m) \sim (n', m') \Leftrightarrow (n',m') \sim (n, m)}$$

　これも明らかです。
  $${n + m' = n' + m\Leftrightarrow n' + m = n + m'}$$
　(=の左右を入れ替えただけ)

③$${{}^\forall (a, b), (c, d), (e, f) \in \mathbb{N}^2 [(a, b) \sim (c,d),   (c,d)\sim (e, f)\Longrightarrow (a, b) \sim (e, f)]}$$

  仮定を満たすとき、次の二つの等式が成り立ちます。
　(1)$${a + d = c +  b}$$
  (2)$${c + f = e + d}$$
　この時、

$$
a + f + d = a + b + f \underset{(1)}{=} c + b + f
= c + f + b \underset{(2)}{=}e + d + b = e + b + d
$$

より$${a +f = e + b}$$を得られ、$${(a, b) \sim (e, f)}$$がわかります。

これで、同値関係～が手に入ったので、商集合が考えられますね。
それを整数の集合としましょう。

これで整数の集合$${\mathbb{Z}}$$が作れましたね。
下に$${\mathbb{Z}}$$の構成のイメージを置いときます。

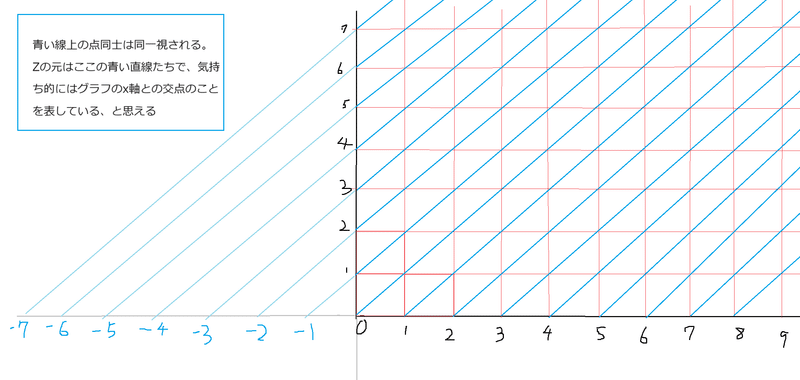
足し算の定義

集合$${\mathbb{Z}}$$を定義できたので、次は足し算を自然に定義しましょう。
$${(n, m), (n', m') \in \mathbb{N}^2}$$に対して、それぞれ$${n - m , n'-m'}$$と思えたわけですね。では、この二つの和はどうなってほしいでしょうか？

符号ごとに計算しちゃって、$${n+n'-(m+m')}$$としてしまえばいいですね。これは$${(n+n', m+m')}$$に対応した数ですから、
単に$${(n, m)}$$と$${(n', m')}$$の和は $${(n+n', m+m')}$$にしてやればいいでしょう。
これと同じことを、商集合$${\mathbb{Z}=\mathbb{N}^2 / \sim}$$でも考えられます。
では定義しましょう。

確認しないといけないのは、この足し算がwell-definedであるか、つまり
$${(a, b) \sim (a', b'),  (c, d) \sim (c', d')}$$の時に
$${[(a+c, b+d)]}$$と$${[(a'+c', b'+d')]}$$が一致するかどうかです。
もし一致しなかったら、$${\mathbb{Z}}$$の２つの要素に対してそれぞれの代表元の取り方によって足し算の結果が変わってしまいます。
(3-1) + (2-1)と(4-2) + (2-1)の値が違うとか困りますよね？
（$${\mathbb{Z}}$$上では）同じものなのに、結果が異なるなんてことは起きてほしくないんです。

では証明しましょう。

$${(a, b) \sim (a', b'),  (c, d) \sim (c', d')}$$と仮定しましょう。この時に、
$${[(a+c, b+d)] = [(a'+c', b'+d')]}$$, つまり$${(a+c, b+d) \sim (a'+c', b'+d')}$$を示せばOKです。

仮定から、$${a+b' = a' + b,   c + d'=c' + d}$$が成り立ちます。
ここで、
$${(a + c)+ (b'+ d')= (a + b')+ (c + d')\\\underset{仮定}{=} (a'+ b)+(c'+ d)= (a' + c')+ (b + d)}$$
であり、この最左辺と最右辺を見て、$${(a+c, b+d) \sim (a'+c', b'+d')}$$が得られました。

これで整数の集合$${\mathbb{Z}}$$に足し算を入れられましたね。
証明は省きますが、この足し算は交換法則、結合法則が成り立ちます。
自然数の足し算についてこれらが成り立つことに注意すれば証明できるので試してみてください。

また、$${[(0, 0)] \in \mathbb{Z}}$$はどの数に足しても値に変化を及ぼしません。

そしてこれが一番欲しかった結果です。
任意の$${\mathbb{Z}}$$の要素$${[(n, m)]}$$に対し、$${[(m, n)]}$$は足し算に関する逆元になります。つまり
$${[(n, m)] +_\mathbb{Z} [(m, n)] = [(0, 0)]}$$
が成り立ちます。（自然数$${k}$$について$${[(k, k)]= [(0, 0)]}$$となることを定義通りに確かめればあとは計算）

どうでしょう？自分たちが知っている「マイナスの数」のイメージ的に、
$${[(n, m)]}$$のマイナスの数は$${[(m, n)]}$$としてよさそうですね。

ということで、$${x = [(n, m)] \in \mathbb{Z}}$$に対し
$${x  +_\mathbb{Z}  a= [(0, 0)]}$$
を満たすような$${a}$$　（つまり[(m, n)]のこと）
を$${-x}$$と表すことにしましょう。

話の順序が入れ替わってしまいましたが、$${\mathbb{Z}}$$の要素に対し、その「マイナスの数」は一つに定まります。だから上のようにその数を表す記号を作っても問題ないですね。

引き算の定義

では待ちに待った引き算の定義と行きましょう。
皆さん、引き算ってどんなものでしたっけ？　引き算のことに関しては大半の人が良く知っていますね。
「a - b」と言われれば、その意味を言葉で説明するなら、「bに何を足したらaになる？の答え」になりますよね。この言葉の通りに定義してやりましょう。上の「マイナスの数」のおかげで、僕たちはその「答え」を明示的に書くことができます。
では定義しましょう

＋とーの横にちょっとついてる$${\mathbb{Z}}$$のマークは、今の時点では自然数の和と区別するためにつけてますが、最終的にはとれる（区別がいらなくなる）ので、しばらく我慢してください！

実際、定義した右の数は、
「$${y}$$に何を足したら$${x}$$になる？」の答えになっていますね。

なので引き算の定義としてはこれが妥当でしょう。

ℤ上の掛け算

掛け算も定義しておきましょう。考え方は足し算の時と同じです。
すでに$${\mathbb{Z}}$$上の引き算は定義されてますが、自然数の集合と整数の集合の関係についてはまだ触れていないので、自然数同士に、定義された引き算を自然に適用させられることがまだ言えません。
なので一旦形式的な引き算のまま考えるとしましょう。
$${(n, m), (n', m') }$$はそれぞれ形式的引き算で$${n - m, n' - m'}$$と思っていました。この二つの掛算はどうしましょうか？
普通に計算したら$${(nn'+mm')-(nm' + n'm)}$$となりますね。これを見ながら$${\mathbb{Z}}$$上の掛算を定義しましょう。

足し算の時と同様に、welldefinedかどうかを確認します。大事なので書いときますが計算が面倒なだけなので飛ばしてもらって結構です。

$${(a, b) \sim (a', b'),   (c, d) \sim (c', d')}$$とする。この時に
$${(ac+bd, ad+cb) \sim (a'c'+b'd', a'd'+c'b')}$$,つまり
$${ac+bd + a'd'+c'b' = ad+cb+a'c'+b'd'}$$を示す。
仮定を満たすとき
$${a+b' = b+a'}$$
$${c+d'=d+ c'}$$
が成り立つことに注意。
頑張って計算して、

$$
・\underset{左辺}{(ac+bd + a'd'+c'b' )}+(cb'+ac'+bd'+a'd) = (a+b')(c+c') + (b+a')(d+d')\\ \underset{仮定}{=} (a+b')(c+c')+ (a+b')(d+d')= (a+b')(c+d+c' + d')\\
 \\
・\underset{右辺}{(ad+cb + a'c'+b'd' )}+(cb'+ac'+bd'+a'd) = b(c + d') + a'(d+ c') + a(d + c') + b'(c + d')\\ \underset{仮定}{=}  b(c + d') + a'(c+ d') + a(d+ c') + b'(d+ c')=(b+a')(c+ d')+ (a+b')(d+c')\\= (a+b')(c+ d')+ (a+b')(d+c')= (a+b')(c+d+c'+d')

$$

より$${\underset{左辺}{(ac+bd+ a'd'+c'b' )}+(cb'+ac'+bd'+a'd)=\underset{右辺}{(ad+cb + a'c'+b'd' )}+(cb'+ac'+bd'+a'd) }$$がわかり、
よって主張の左辺＝右辺がいえました。

かけざんの定義を見ると明らかに交換法則が成り立ちますね。それから証明は省きますが、結合法則も成り立ちます。さらに上で定義した足し算について分配法則も成り立ちます。
結合則、分配則の証明は６種類の記号が絡んだ鬼のような計算なので、計算するのが好きな人だけやってみてください。僕はやりたくないです

それから、[(1, 0)]はほかのどの$${\mathbb{Z}}$$の要素にかけても変化を及ぼしません。これは簡単な計算でできるので確認してみてね

ℤの大小関係

ここは軽く定義だけしましょう。
ここも形式的な引き算を見ながら考えれば自然に大小関係が見えてきます。

計算頑張れば証明できるとだけ言って略しますが、これはwell-definedな全順序関係となります。

自然数の集合と整数の集合の関係性

皆さんの知っている整数の集合$${\mathbb{Z}}$$は、自然数を含んでいましたよね？
しかし、この記事の定義を見ると、明らかに自然数は$${\mathbb{Z}}$$に入っていません。
しかし、$${\mathbb{Z}}$$の中には、$${\mathbb{N}}$$と同じ構造を持つ部分集合Aが存在します。
数学をする上では、構造さえ変わらずにいてくれれば、基本的に中身が変わろうが問題ありません。なので、各自然数nに対し、nと「Aの中でnに対応する元」を名前が変わっただけの同じものとみなし、実質的に$${n \in \mathbb{Z}}$$と思えるんですね。

では、その部分集合Aをちゃんと特定し、特にそれぞれの自然数がどの元に対応しているのかをはっきりさせておきましょう。

証明は計算して確かめればOKです。
これにより、上で定義した$${\iota}$$による$${\mathbb{N}}$$の像、すなわち$${\{[(n, 0)] | n \in \mathbb{N}\}}$$が$${\mathbb{N}}$$と同型な集合になります。これにより、自然数nと[(n, 0)]を同じものとみなし、nを整数として扱えるようになりました。
ここにきて、今まで形式的にしか考えてこなかった自然数の引き算が意味を持つようになります。
$${n, m \in \mathbb{N}}$$に対して、[(n, m)]はn - m のことだと思っていました。今では自然数に引き算が使えるので、計算してみましょう。
$${n- m = [(n, 0)] - [(m, 0)] = [(n, 0)] + [(0, m)] = [(n, m)]}$$
となりました。
$${\mathbb{Z}}$$を作るときの気持ちはちゃんと$${\mathbb{Z}}$$に反映されていましたね。めでたしめでたし。

これが最後です。
$${\mathbb{Z}}$$の元[(n, m)]は、自然数の順序の全順序性から
$${n = m +k (k \in \mathbb{N})}$$と表せるか、
$${m = n +k (k \in \mathbb{N})}$$と表せるかの少なくとも片方が成り立ちます。
前者の時は、[(n, m)]= [(k, 0)]となり、上で話した同一視のもと[(n, m)]は自然数といえます。
後者の場合は、[(n, m)]= [(0, k)]となり、これは (k =)[(k, 0)]の「マイナスの数」となります。
つまり、$${\mathbb{Z}}$$の元は[(k, 0)]か[(0, k)]の形でいつでも表せるわけです。

自然数nについて、それに対応する元[(n, 0)]のことをなりふり構わずnと書くことにし、nのマイナスの数（すなわち[(0, n)]）を-nとあらわすことにしましょう。
そのうえでさっきの話をまとめると、
$${\mathbb{Z} = \mathbb{N} \cup \{ -n | n \in \mathbb{N}\}}$$、
つまり整数は、自然数及びそのマイナスの数のみを含むことがわかります。
言い換えるなら、$${\mathbb{Z}}$$は$${\mathbb{N}}$$にマイナスの数を追加した集合になりますね！なので冒頭で話した目標が達成できました。

これで、整数の集合$${\mathbb{Z}= \{\cdots -3, -2, -1, 0, 1, 2, 3 \cdots\}}$$が手に入りましたね。
これで、例えば「なんでマイナス×マイナスはプラスなの？」と聞かれても定義を見せればいいのでごまかす必要はありませんね！
まあ、マイナス×マイナスがプラスになる前提で作った定義だから納得させることはたぶん無理ですけどね。
なにはともあれ整数の集合及びその演算を作ることはできました。

次は整数から有理数を作る話をすると思います。
ここまで読んでくれた方はありがとうございました。