微分の計算には変化の割合、横幅をゼロに限りなく近づけるという考え方を使います。
今回は、これらを使ってどのように考え、微分によりかなり小さい変化の計算をするのか解説します。

以下では、前回と同じようにグラフを使います。ここでも前回と同じように横軸を$${ x}$$、縦軸を$${ y}$$とします。
また横方向を$${ x}$$方向、縦方向を$${ y}$$方向と言います。

微分の計算方法

次の、

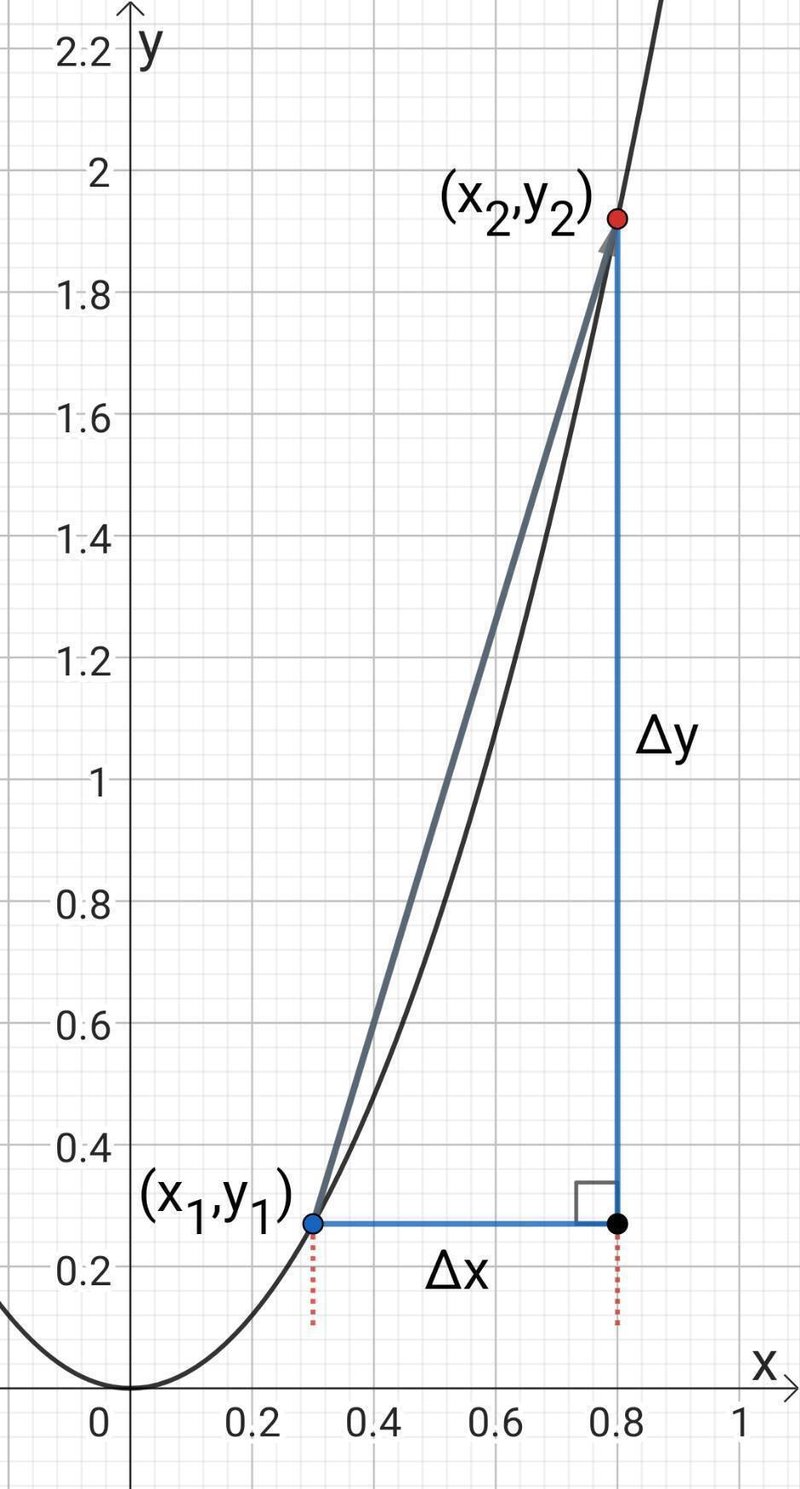
のように青い点が黒線上を動き、赤い点の場所まで動いた場合を考えます。
以下では青い点を動かすとき、必ず黒線上を動くとします。
また青い点の座標を$${ (x_1,y_1)}$$、赤い点の座標を$${(x_2,y_2)}$$、縦幅を$${ \Delta y}$$、横幅を$${ \Delta x}$$とし、２本の縦の赤線間の距離も横幅を表しています。
このときデルタを使うと、
$${ x}$$の増加量$${ =\Delta x }$$
$${ y}$$の増加量$${ =\Delta y }$$
となるので、
変化の割合$${ =\dfrac{ \Delta y}{ \Delta x}}$$
となります。
また座標を使うと、
$${ x}$$の増加量$${ =x_2-x_1}$$
$${ y}$$の増加量$${ =y_2-y_1}$$
となるので、
変化の割合$${ =\dfrac{ y_2-y_1}{ x_2-x_1}}$$
となります。
これらデルタの場合、座標の場合それぞれの変化の割合を使って、微分の計算によりかなり小さい変化を求めるのか考えてみましょう。
以下ではかなり小さな変化のことを、数学でよく使われる微小変化と言います。

デルタの場合

次の、

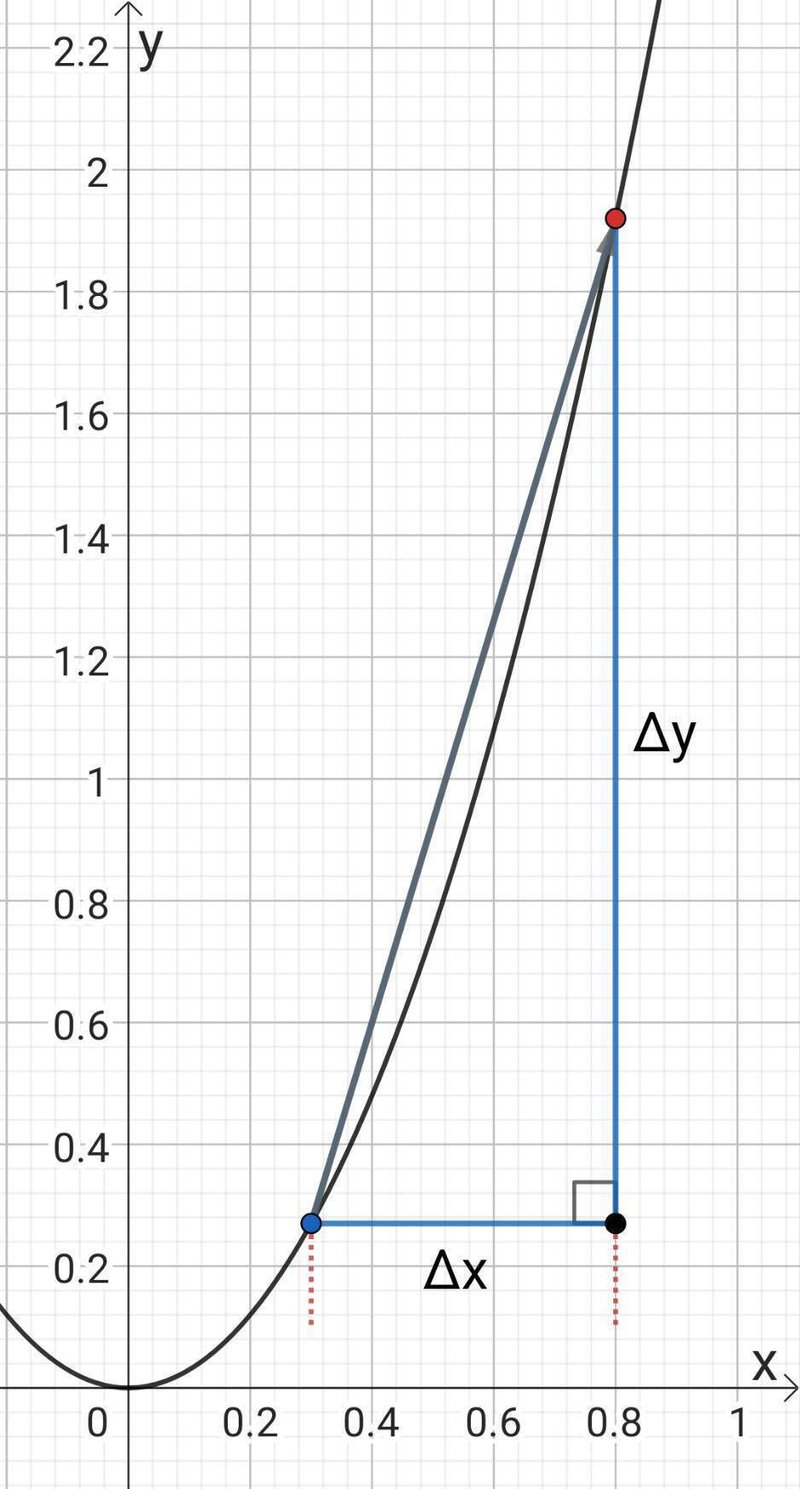
のように青い点が黒線上を動き、赤い点の場所まで動いた場合を考えます。
このときデルタを使うと、
変化の割合$${ =\dfrac{ \Delta y}{ \Delta x}}$$
となります。
微分は、

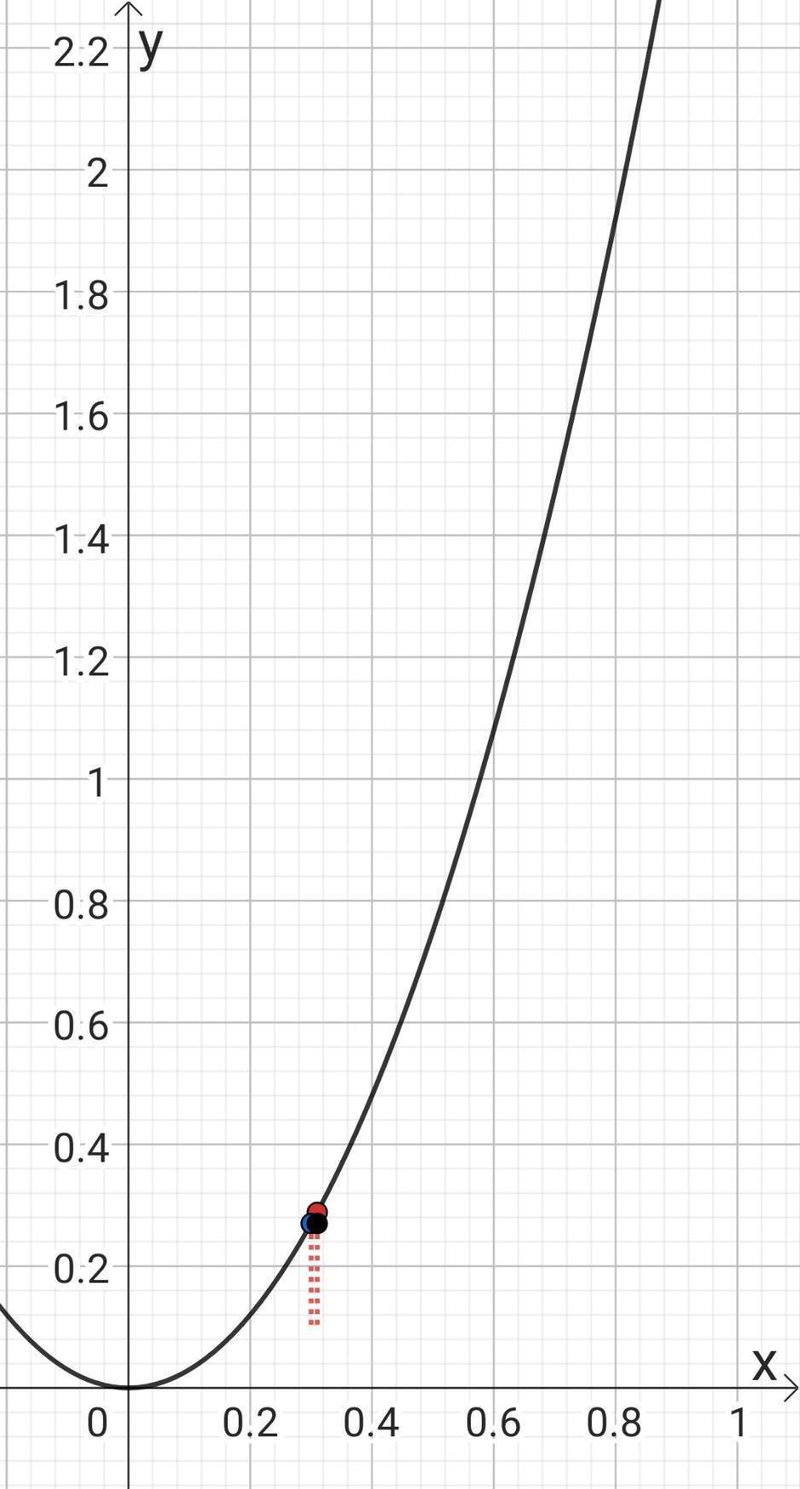
のように横幅を、
ゼロに限りなく近づける
場合を考えます。
これらを使い、微分の計算を考えることができます。
変化の割合とは、
$${ x}$$方向に$${ \Delta x}$$変化したとき
を考えています。
微分を考えるときは横幅$${ \Delta x}$$を、
ゼロに限りなく近づける場合
となります。
これらから微分は、
$${ x}$$方向の変化$${ \Delta x}$$をゼロに限りなく近づける場合
を考えることになります。
つまり微分は、変化の割合の横幅である$${ \Delta x}$$を、
ゼロに限りなく近づける場合
を計算します。
このことを数学では、
$${\displaystyle \dfrac{ d y}{ d x}=\lim_{\Delta x \to 0}{\dfrac{ \Delta y}{ \Delta x}}}$$
のように数式で表現をします。
ここで、
$${\dfrac{ d y}{ d x}}$$
は微小変化を表しています。
この$${ d}$$は、微分を英語でdifferentialと言うので、この頭文字を使っています。
またこの記号は、
ディーワイ，ディーエックス
と読みます。
分数の形をしていますが、
ディーエックス分のディーワイ
とは読まないので注意しましょう。
また、
$${\displaystyle \lim_{\Delta x \to 0}}$$
は、
$${ \Delta x}$$を$${ 0}$$に限りなく近づける
ことを表しています。
$${ \lim}$$は限界という意味であるlimitを略したもので、数学では極限という意味となります。
これらから微分の計算をするときは、
変化の割合$${ =\dfrac{ \Delta y}{ \Delta x}}$$
の式の、
$${ \Delta x}$$を$${ 0}$$に限りなく近づける
という意味である、
$${\displaystyle \dfrac{ d y}{ d x}=\lim_{\Delta x \to 0}{\dfrac{ \Delta y}{ \Delta x}}}$$
の計算をし、微小変化を求めます。

座標の場合

次の、

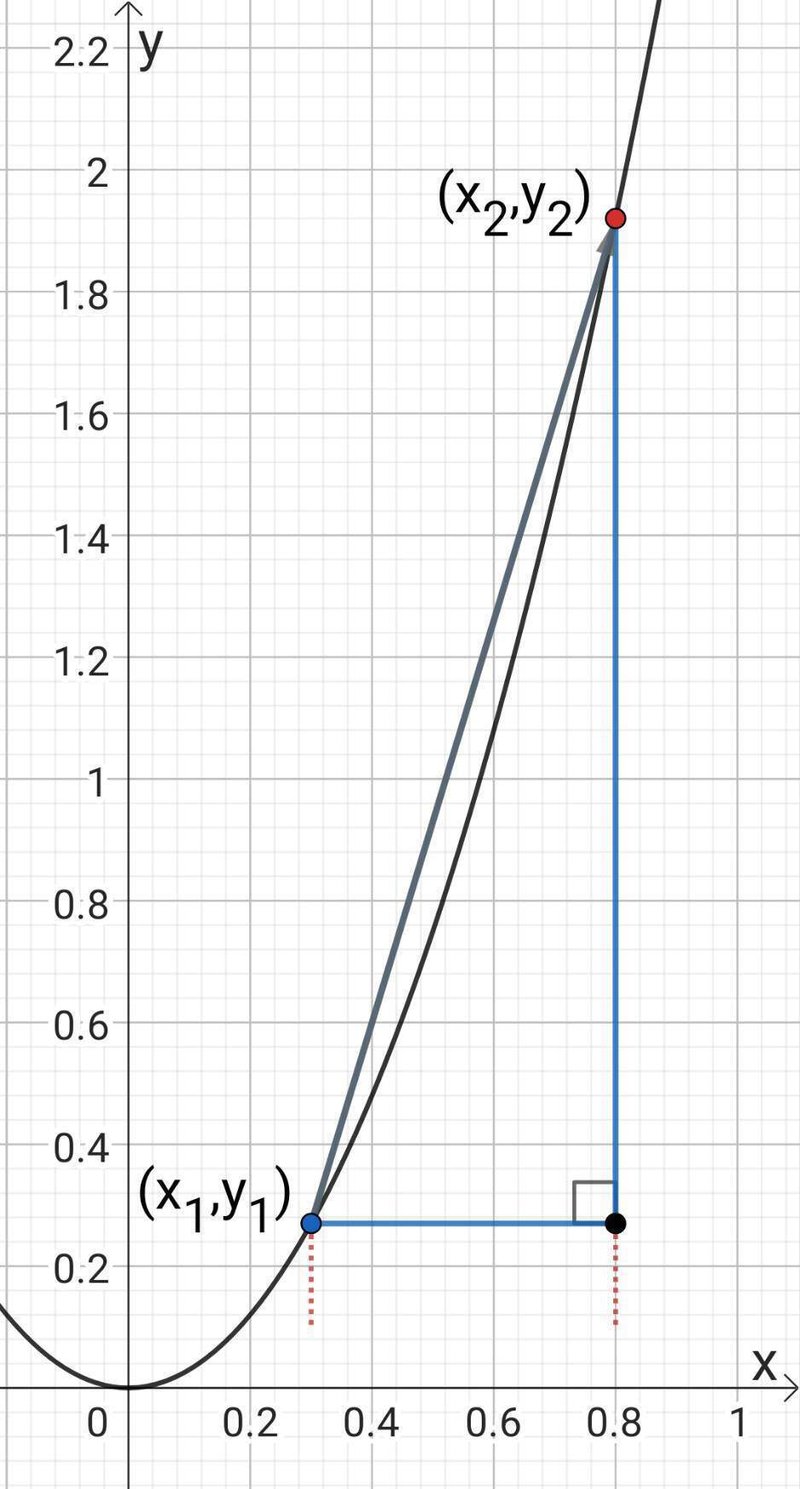
のように青い点が黒線上を動き、赤い点の場所まで動いた場合を考えます。
このとき、青い点と赤い点それぞれの座標$${ (x_1,y_1),(x_2,y_2)}$$を使うと、
変化の割合$${ =\dfrac{ y_2-y_1}{ x_2-x_1}}$$
となります。
微分は、

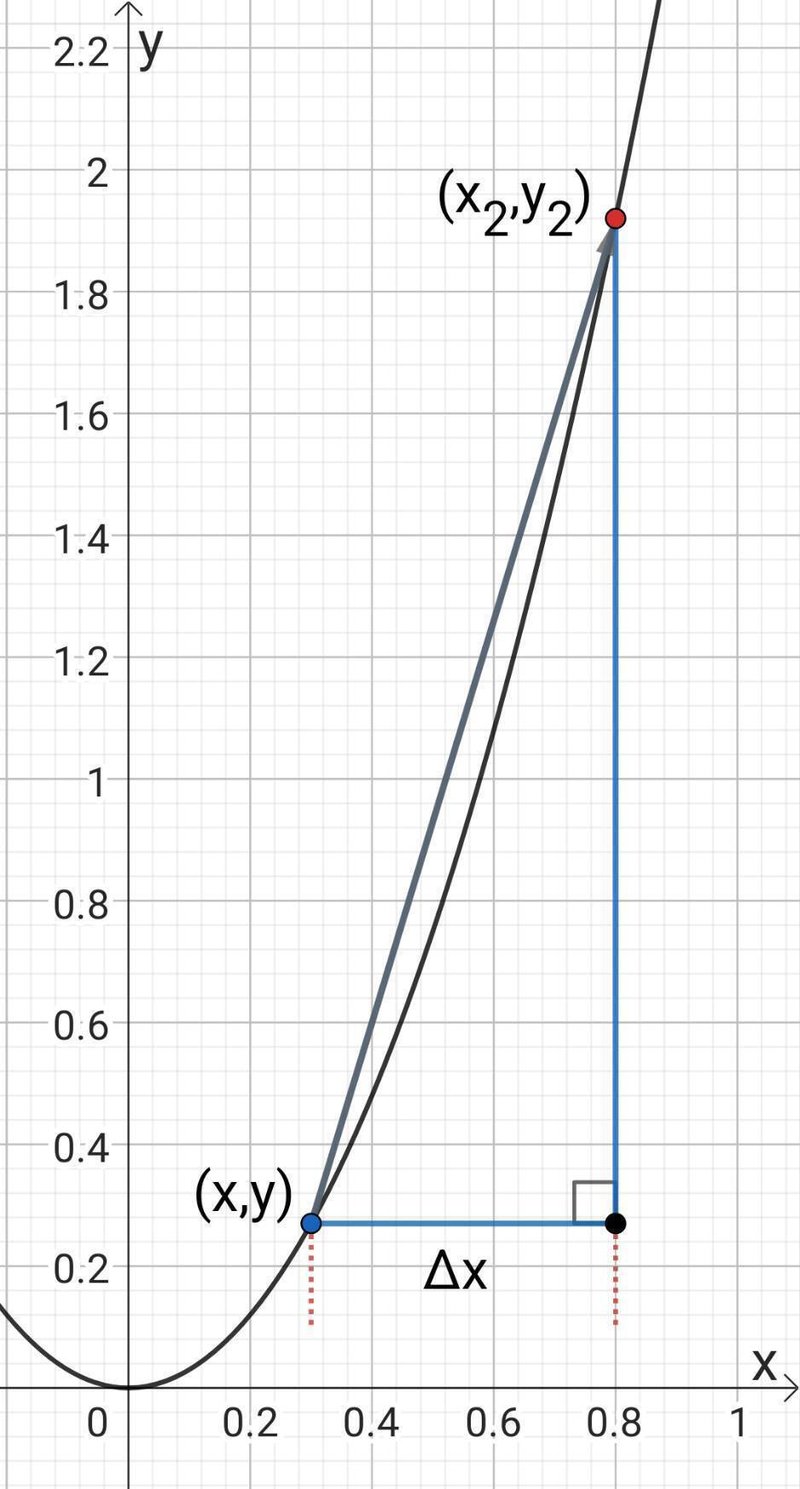
のように青い点の座標を$${(x,y)}$$、赤い点まで$${ x}$$方向に$${ \Delta x}$$動かした場合を考えます。
このとき、
変化の割合$${ =\dfrac{ y_2-y_1}{ x_2-x_1}}$$
の式で、$${ (x_1,y_1)}$$は青い点の座標、$${ (x_2,y_2)}$$は赤い点の座標なので、
$${ x_1=x,x_2=x+\Delta x}$$
となり、
$${ x_2-x_1=(x+\Delta x)-x=\Delta x}$$
となります。
これらから、
変化の割合$${ =\dfrac{ y_2-y_1}{ x_2-x_1}=\dfrac{ y_2-y_1}{ \Delta x}}$$
となります。
このときグラフの式を、
$${ y=3x^2}$$
とすると、
$${ x_1=x,x_2=x+\Delta x}$$
をグラフの式に代入して、
$${ y_1=3(x_1)^2=3x^2}$$
$${ y_2=3(x_2)^2=3(x+\Delta x)^2}$$
となり、
$${ y_2-y_1=3(x+\Delta x)^2-3x^2}$$
となります。
この式から、
$${ y_2-y_1=x,\Delta x}$$の式
となります。
これらから変化の割合は、グラフの式がわかると$${ x,\Delta x}$$を使って表すことができます。
この変化の割合の式で、
$${ \Delta x}$$を$${ 0}$$に限りなく近づける
という計算をし、微小変化を求めます。
このことは数式では、
$${\displaystyle \dfrac{ d y}{ d x}=\lim_{\Delta x \to 0}{\dfrac{ x, \Delta xの式}{ \Delta x}}}$$
の計算をすることになります。

まとめ

今回は変化の割合、横幅をゼロに限りなく近づけるという考え方を使ってどのように考え、微分により微小変化の計算をするのか解説しました。
微分の計算は、

1. 変化の割合をグラフの式を使って、$${ x,\Delta x}$$で表す

2. $${ \Delta x}$$を$${ 0}$$に限りなく近づけるという計算をする

という、
$${\displaystyle \dfrac{ d y}{ d x}=\lim_{\Delta x \to 0}{\dfrac{ x, \Delta xの式}{ \Delta x}}}$$
の計算をして、微小変化を求めます。

次回は、これらのことを使って具体的に、$${ a}$$を定数として、
$${y=x^2,y=x,y=a}$$
のような$${ y}$$が二次式、一次式、定数の場合の微小変化を求めます。
これらの微小変化を求めることにより、今回の内容がよくわかるようになると思います。
また、今回からかなり小さな変化を微小変化と言うようにしました。
この理由としては、最初のほうは数学用語をあまり使わないようにしていました。
しかし、今は数学の色を濃くしているため、微小変化という言葉を使うようにしました。
ここで微分の計算で求めた結果は、微小変化よりふさわしい用語があります。
しかし今回は、微分によりかなり小さい変化が求められると表現をしたため、かなり小さい変化に対応する用語として微小変化を使っています。
微分を知っている人には、違和感があるかもしれませんが、許していただければと思います。