三角比を勉強し始めると、
そのうち三角形の面積の公式が出てきますよね。
今までは
底辺×高さ÷2
だったのが、ガラッと変わります。
その仕組み、意外と知らない人も多いかもしれないので、
ここで見ていきましょう。

公式の確認

まずはどんな公式か、確認しましょう。

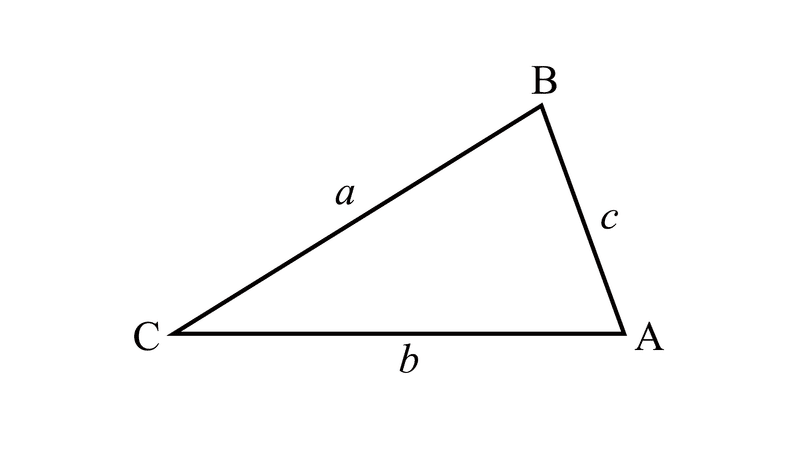
こんな三角形があったとして、面積$${S}$$は、

$$
S=\frac{1}{2}bc\sin{A}
$$

です。
要は、2つの辺をかけて、その間の$${\sin}$$をかけて半分にするということ。
割と単純ですので、
使いこなすまでに、そう時間はかからないと思います。

実はこれ、今までやっていた

$$
S=底辺×高さ×\frac{1}{2}
$$

とほとんど同じ意味なのです。
その理由は次の通り。

公式が成り立つ理由

まず、$${\mathrm{B}}$$から$${\mathrm{AC}}$$に垂線をおろすと、

こんな風になりますよね。
ここで、

$$
BD=c\sin{A}
$$

となりますよね。
こうしてしまえば、従来の

$$
S=底辺×高さ×\frac{1}{2}
$$

で計算できます。
すると、

$$
S=\frac{1}{2} \cdot b \cdot c \sin{A}
$$

となり、公式が出てくるわけです。
シンプルですね！

更にヘロンの公式へ

ここまでの公式では、$${\sin{A}}$$を使用していました。
つまり、どこかの角度の$${\sin}$$が分からないと面積が求まらないわけです。
でも、$${\sin}$$や$${\cos}$$は、全部の辺が分かっていたら出せますよね。
てことで、次のようになります。

$$
\def\arraystretch{3}
\begin{align}
S &= \frac{1}{2}bc \sin{A} \nonumber \\
&= \frac{1}{2}bc \sqrt{1- \cos^2{A}} \nonumber \\
&= \frac{1}{2}bc \sqrt{1- \left( \frac{b^2 + c^2 -a^2}{2bc} \right) ^2} \nonumber \\

&= \frac{1}{2}bc \sqrt{
\left[ 1+ \left( \frac{b^2 + c^2 -a^2}{2bc} \right) \right]
\left[ 1- \left( \frac{b^2 + c^2 -a^2}{2bc} \right) \right]
} \nonumber \\

&= \frac{bc}{2} \sqrt{
\left[ \frac{2bc+ b^2 + c^2 - a^2}{2bc} \right]
\left[ \frac{2bc - b^2 - c^2 + a^2}{2bc} \right]
} \nonumber \\

&= \frac{bc}{2} \frac{1}{2bc} \sqrt{
\left[ b^2 +2bc + c^2 - a^2 \right]
\left[ a^2 - (b^2 -2bc + c^2) \right]
} \nonumber \\

&=\frac{1}{4}\sqrt{
\left[ (b+c)^2 - a^2 \right]
\left[ a^2 - (b-c)^2 \right]
} \nonumber \\

&=\frac{1}{4}\sqrt{
\left[ (b+c + a)(b+c-a) \right]
\left[ (a+ b-c)(a-b+c) \right]
} \nonumber \\

&=\frac{1}{4}\sqrt{
(a+b+c)(a+b-c)(b+c-a)(c+a-b)
} \nonumber \\
\end{align}
$$

長いですけど、最後は割とスッキリしました！

ここで、なぜか

$${s=\frac{a+b+c}{2}}$$

とおいて、式を書き換える作業をするのが、
多くの教科書に書いてあるヘロンの公式です。
どういうことかというと、まず、

$$
\def\arraystretch{3}
\begin{align}
S&= \frac{1}{4}\sqrt{
(a+b+c)(a+b-c)(b+c-a)(c+a-b)
} \nonumber \\

&= \sqrt{
\frac{a+b+c}{2} \frac{a+b-c}{2} \frac{b+c-a}{2} \frac{c+a-b}{2}
} \nonumber \\

\end{align}
$$

と変形して、ここで、

$$
\def\arraystretch{3}
\begin{align}

\frac{a+b+c}{2} &=s \nonumber \\
\frac{a+b-c}{2} &=\frac{a+b+c-2c}{2} = s-c \nonumber \\
\frac{b+c-a}{2} &=\frac{a+b+c-2c}{2} = s-a \nonumber \\
\frac{c+a-b}{2} &=\frac{a+b+c-2c}{2} = s-b \nonumber \\

\end{align}
$$

より、

$$
\def\arraystretch{3}
\begin{align}

S&= \sqrt{
\frac{(a+b+c)}{2} \frac{(a+b-c)}{2} \frac{(b+c-a)}{2} \frac{(c+a-b)}{2}
} \nonumber \\

&=\sqrt{s(s-a)(s-b)(s-c)} \nonumber

\end{align}
$$

となるわけです。
この最後に出てきた、

$$
S=\sqrt{s(s-a)(s-b)(s-c)}
$$

がヘロンの公式と言われるものですね。
まあ、覚えなくていいです。
上の方でやったように、
$${\sin}$$、$${\cos}$$がきちんと出せて、
$${S=\frac{1}{2}bc\sin{A}}$$のやり方を身に付けていることの方が大事です。