高校生の子供が駿台全国模試を受けるようになりました。結果が帰ってきた時には偏差値を見るのですが、自分が高校時代に受けていたのが河合塾の全統記述模試だったので、数字をみても、どうにも直感的にわかりません。

2つの模試では母集団が違うので、もちろん偏差値の変換は厳密にはできません。ただ、インターネット上では、「駿台全国模試＝全統記述模試−10」とか「全統記述模試ー7＝駿台判定模試＝駿台全国模試＋3」（⇔駿台全国模試＝全統記述模試−4）というような偏差値変換の記述が書き込まれています。

「この変換式のマイナス10とかマイナス4とかの数字は妥当か？根拠有るのか？」と思い、自分でデータを集めて検証してみました。やっていることは、統計の初歩の回帰分析だけです。

0. 結論（全統記述模試と駿台全国模試の偏差値変換モデル）

ざっくり言うと、全統記述模試の偏差値45〜70の範囲なら「駿台全国模試＝全統記述模試ー4」でした。逆に見れば、駿台全国模試の偏差値が41〜66の範囲で「全統記述模試＝駿台全国模試＋4」となります。

分析から考案した変換モデルは以下となります。全統模試の偏差値をK、駿台全国模試の偏差値をSで表現しています。^記号は累乗です（S^2はSの2乗）。

◆概算する場合

全統記述模試の偏差値
40未満： S = K ＋5
40以上45未満： S = K ＋ 1
45以上50未満： S = K ー 2
45以上50未満： S = K ー 2
50以上55未満： S = K ー 4
55以上60未満： S = K ー 5
60以上65未満： S = K ー 5
65以上70未満： S = K ー 4
70以上： S = K ＋ 3
※45以上70未満の区間の平均で、S = K ー 4

◆回帰式で計算する場合

• K ＝ -0.0196 x S^2  +  3.1496 x S -54.121　
  （二次回帰、相関係数＝0.9937）

• S = 0.0191 x K^2 - 1.189 x K + 57.944
  （二次回帰、相関係数＝0.9856）

1. 変換モデルの考え方

「全統記述模試と駿台全国模試は模試を受験する母集団の特性が違うので、2つの模試の偏差値は比較できない」というのが一般論です。実際に東大理一のボーダー偏差値も、全統記述模試では70（C判定50％）に対して、駿台全国模試では68（B判定60％）と違います。

でも、模試を受験した母集団は違っても、その中の標本としての「全統記述模試の受験者のうち東大理一の受験者の標本」と「駿台全国模試の受験者のうち東大理一の受験者の標本」は、「東大理一の受験者」という同じ母集団にも属するはずです。つまり、それぞれは「東大理一の受験者のうち全統記述模試の受験者の標本」と「東大理一の受験者のうち全統記述模試の受験者の標本」とも言えるはずです。

そうであれば、それぞれの予備校が過去の統計から算定して同じ合格率になる偏差値であれば、模試が違っても東大理一受験者の母集団の中では同じ学力の集合になるはずです。こう考えると、何らかのやり方で、2つの模試の偏差値を変換することはできそうです。

ただ、全統記述模試と駿台全国模試では、ボーダー偏差値の合格率の設定が違うため、この補正が必要です。全統記述模試では、B判定65％とC判定50％の偏差値の差は2.5に固定されています。B判定とC判定の差の15％に占める10％の割合＝2/3を2.5に乗じて、全統記述模試の60％合格率の偏差値を71.7としました。

この場合、全統記述模試の合格率60％偏差値71.7＝駿台全国模試の合格率偏差値68.0という変換式になります。

ところが、全統記述模試では東大のボーダーは、理三以外は全て70.0なのに対して、駿台全国模試では文一：67、文二：67、文三：66、理一：68、理二：66とバラバラです。他の大学・学部でも同様に、2つの模試のボーダー偏差値の関係にはバラツキがあります。

バラツキがあるなら、データ数を増やして統計処理をすれば、一般化した変換モデルを作れるはずです。そこで、全統記述模試と駿台全国模試の偏差値の関係を、以下の手順で統計分析してみました。

2. 分析対象の母集団

全統記述模試と駿台全国模試の両方でボーダー偏差値の設定のある国公立大学の学部学科を分析対象としています。私立大学は受験科目の差や入試形式がいろいろあるのと、併願受験ができるので、バラツキが大きくなりすぎる懸念があり、除外しています。

同じ大学でも、学部学科ごとに募集され、ボーダー偏差値が設定されている場合は、異なるデータとして扱います。また、同じ学部学科でも入試形式が違うことがあります。例えば、北海道大学・総合入試理系に化学重点・数学重点などがあるケースです。このように入試形式ごとにボーダー偏差値が設定されている場合は、入試形式ごとに異なるデータとして扱います。さらに、前期日程・後期日程などの違うも異なるデータとして扱います。

結果、分析対象の母集団は125大学の1,911データとなっています。

データは2つの変数を持ちます。1つは全統記述模試の60％合格率偏差値（C判定＋1.7）、もう1つは駿台全国模試の60％合格率偏差値（B判定）です。全統記述模試は2023年7月時点、駿台全国模試は2023年3月時点のボーダー偏差値の数値を採用しています。

データのサンプルはこのようなものになります。前にある数字が全統記述模試の偏差値、後ろにある数字が駿台全国模試の偏差値です。

• 東京大学理科一類・前期：（71.7、68）
  ※類型で募集、前期日程のみ

• 横浜市立大学・国際教養学部・国際教養学科・A方式・前期：（59.2、52）

• 横浜市立大学・国際教養学部・国際教養学科・B方式・前期：（64.2、53）
  ※方式ごとにデータを作る

• 一橋大学・経済学部・経済学科・前期：（66.7、63）

• 一橋大学・経済学部・経済学科・後期：（74.2、71）
  ※前期と後期にわけてデータを作る

3. データ分布と回帰分析

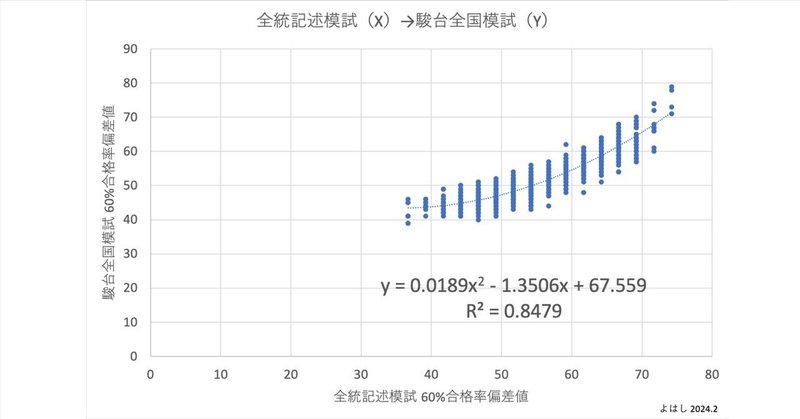
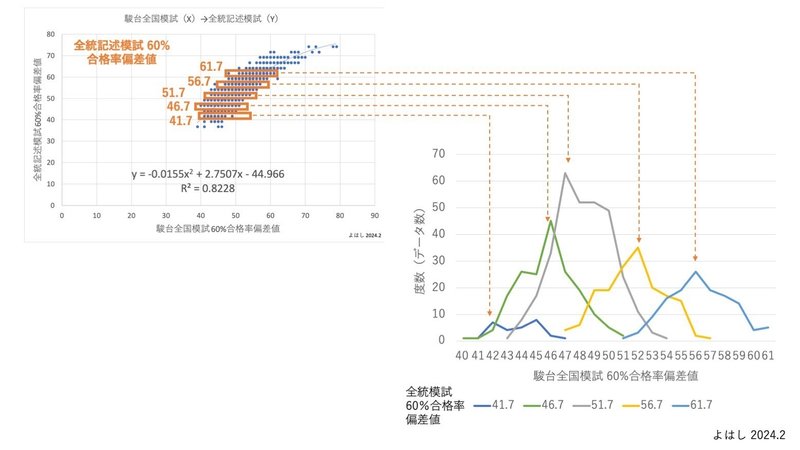
この母集団（1,911データ）に対して、横軸（X）を全統記述模試の60％合格率偏差値、縦軸（Y）を駿台全国模試の60％合格率偏差値とした場合、散布図はこうなります。回帰分析は1次回帰より2次回帰の方が相関係数が高いため、2次回帰で回帰式を算定しています。

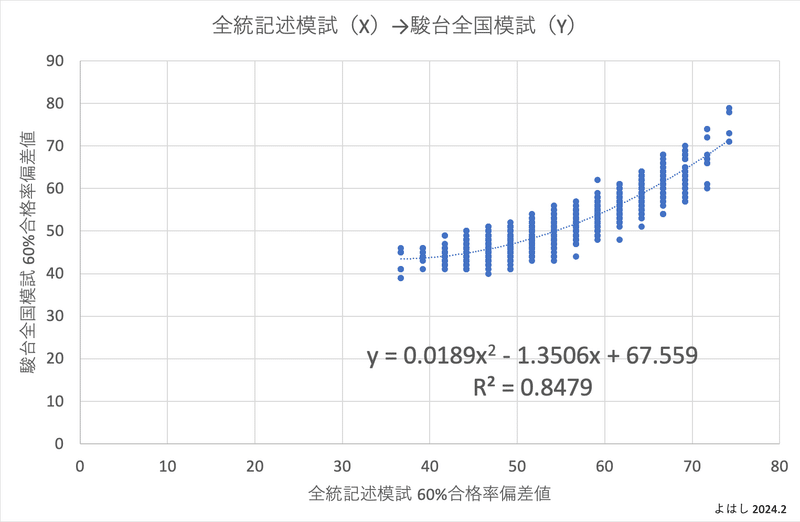
同じ母集団に対して、横軸と縦軸を逆転させた散布図はこうなります。

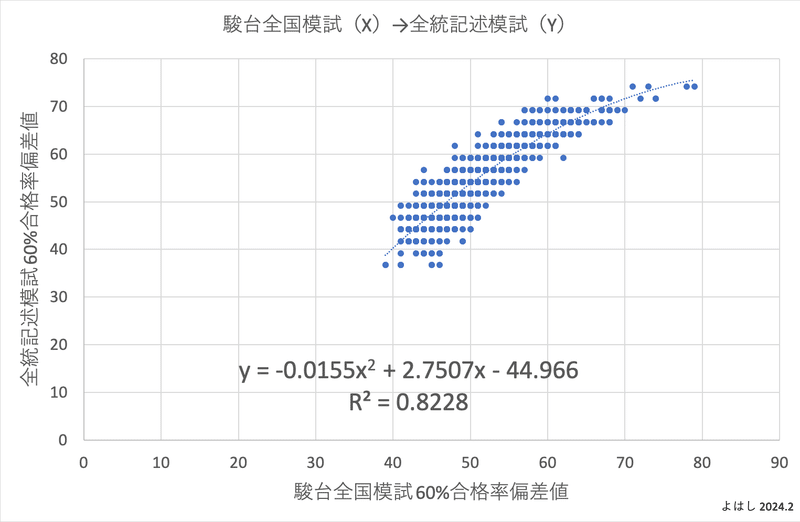
どちらを見ても、2つの模試の偏差値には一定の相関があることがわかります。ただ、全統記述模試のボーダー偏差値が2.5刻みなので、同じ全統記述模試の偏差値でも、駿台全国模試の偏差値は10程度の幅で分布してしまっています。

これに対して、もう一段の統計処理を行います。

4. 同一偏差値の標本の分布

グラフ2のY軸（全統記述模試の60％合格率偏差値）が、51.7（C判定50.0）のデータを抽出した標本を作ってみます。この標本には、例えば、以下のようなデータが含まれます。

• 東京農工大・農学部・地域生態システム学科・前期：（51.7、54）

• 岐阜大学・工学部・化学学科・生命化学・前期：（51.7、48）

• 北九州大学・国際環境工学部・情報システム学科・後期：（51.7、43）

この標本（全統記述模試の60％合格率偏差値＝51.7）には、317のデータが含まれています。そのデータを、駿台全国模試の60％合格偏差値ごとに度数集計したヒストグラムはこうなります。

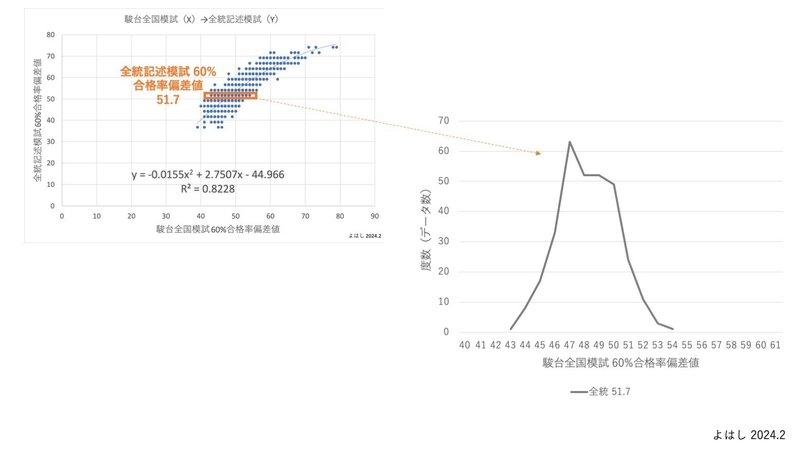
正規分布にかなり近い分布をしていることが見てわかると思います。検証のために、他の偏差値帯でも同じようにヒストグラムを作ってみると、同様に正規分布に近い分布をしています。

全統記述模試の60％合格率偏差値が同じ数値のデータを抽出しているので、この標本は無作為抽出ではありません。ただ、河合塾でボーダー偏差値を設定した社員が、標本の大学・学部・学科に対して有為に同じボーダー偏差値を設定したとは考えにくいです。結果として、偶然にも同じボーダー偏差値が設定され、この標本ができたと考える方が自然です。

そして、この標本はそこに含まれる大学・学部・学科を受験した学生の母集団が背後にあります。例えば、全統記述模試の60％合格率偏差値が51.7の大学・学部・学科（317データ）を集めた標本は、偏差値51.7（ランク帯なので51.7〜54.2）の学生の母集団から抽出された標本でもあります。

ここで、一つ一つの大学・学部・学科の駿台全国模試の60％合格率偏差値は、そこを受験した受験生の標本平均と同等に扱えると仮定します。これはその偏差値＝標本平均の分布が正規分布になっていることから、中心極限定理を元に、概ね正しと言えそうです。

そうなると、やや強引に中心極限定理を適用すると、それぞれの大学・学部・学科データの駿台全国模試の60％合格率偏差値（＝標本平均）の平均は、全統記述模試の60％合格率偏差値が51.7の受験生全体（＝母集団）の平均値に近似できるのです。

このように考えると、全統記述模試の60％合格率偏差値が同じデータに対して、駿台全国模試の60％合格率偏差値の平均を計算すれば、2つの模試の間の偏差値の変換を行っていることになるのです。

※前に書きましたが、大学で統計学を専攻したわけでなく、2コマしか取っていないので、アカデミズムの文脈で正しいかどうかはわかりません。

5. 同一偏差値の標本平均に対する回帰分析

このロジックを元に、全統記述模試の60％合格率偏差値、駿台全国模試の60％合格率偏差値に対して、同じ数字のデータを集めた標本の平均を使って、散布図と回帰分析をしてみました。

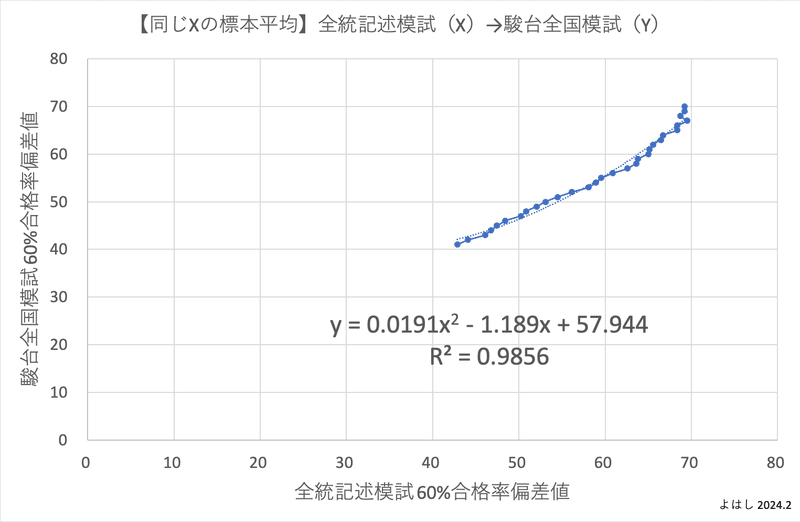
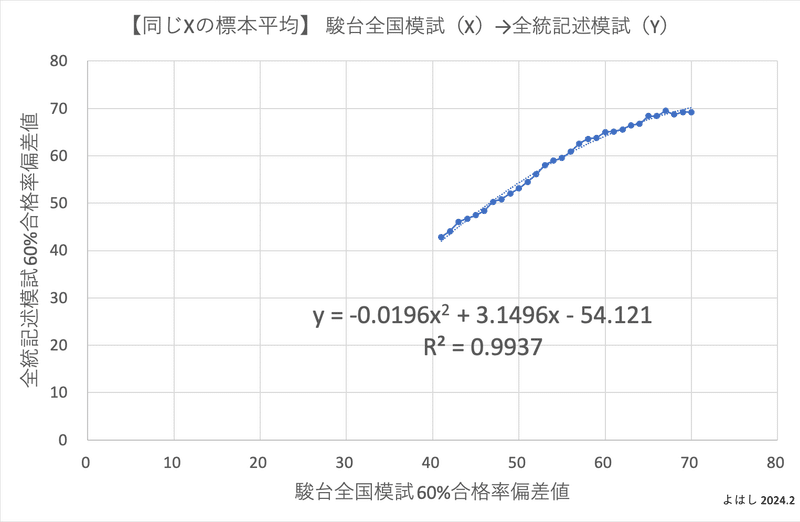
上記の前提が正しければ、このグラフは同じ学力の学生が全統記述模試と駿台全国模試を受験した場合に、それぞれの模試の偏差値がいくつになるかを示しています。そして驚くことに、相関係数は約0.99であり、2つの模試の偏差値はほぼ相関していると言えます。

6. 簡易計算表

上記の通り、全統記述模試の偏差値と駿台全国模試の偏差値は2次回帰式で変換可能であることがわかりました。ただ、2次回帰は計算が一手間かかるので、簡易計算できるようにグラフの点（標本平均のデータ）を集計したのが、この表です。

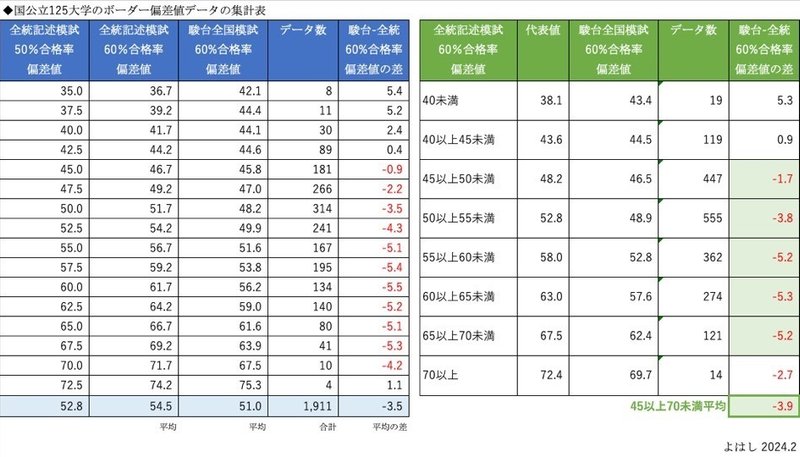
扱いやすいように、全統記述模試の偏差値5の幅で集約しています（緑の表）。たとえば、全統記述模試の偏差値が57.0の人は50以上60未満の幅に入るので、駿台ー全統の偏差値の差は-5.2です。つまり、全統記述模試の偏差値57.0から5.2を引いた51.8が駿台全国模試の偏差値になります。

ただし、40未満と70以上はデータ数が少なく、精度が低いと考えられます。また、45未満は定数の正負が逆転しています。そのため、これらを除外して、全統記述模試の偏差値が45以上70未満の区間（薄緑）で定数を計算すると、-3.9となりました。

つまり、概算であれば、「全統記述模試の偏差値が45以上70未満の区間では、駿台全国模試の偏差値＝全統記述模試の偏差値 − 4」であると言えます。

7. まとめ

全統記述模試と駿台全国模試の変換モデルは、このようになりました。全統模試の偏差値をK、駿台全国模試の偏差値をSで表現しています。^記号は累乗です（S^2はSの2乗）。

◆概算する場合

全統記述模試の偏差値
40未満： S = K ＋5
40以上45未満： S = K ＋ 1
45以上50未満： S = K ー 2
45以上50未満： S = K ー 2
50以上55未満： S = K ー 4
55以上60未満： S = K ー 5
60以上65未満： S = K ー 5
65以上70未満： S = K ー 4
70以上： S = K ＋ 3
※45以上70未満の区間の平均で、S = K ー 4

◆回帰式で計算する場合

• K ＝ -0.0196 x S^2  +  3.1496 x S -54.121　
  （二次回帰、相関係数＝0.9937）

• S = 0.0191 x K^2 - 1.189 x K + 57.944
  （二次回帰、相関係数＝0.9856）

なお、親の世代（1990年代）から子の世代（現在）の間で、大学進学率が上がったことで、模試を受ける母集団が変わっています。おそらく、駿台全国模試の母集団はほぼ変わらず、全統記述模試の母集団が下に膨らんだと思います。

以前に記事にしましたが全統記述模試の偏差値は、今の45以上70未満の区間では、親の世代よりも3〜7くらい大きい数字になります。そのため、ざっくり計算するなら、こんな感じです。

• 全統記述模試の偏差値（現在） ＝ 全統記述模試の偏差値（親の世代）＋5

• 駿台全国模試の偏差値（現在） ＝ 全統記述模試の偏差値（親の世代）＋1

趣味の分析としては以上となります。