私は妻と違って本をそんなに読まない。

妻にとっての本は、エンターテイメントでありファンタジーであり別次元の世界であり、何より居心地の良い大切な場所でもあるように見える。
一方、私はあまり小説なども読まないし、本の世界観に没頭するようなこともあまりなく、どちらかというと情報、辞書的な感じで使うことが多い。
色んな観点で物事をみたり、興味ある分野の情報を集めたい人なので、買ってはみたが読めてない本もたくさんある。

そんな私でも、「人生を変えた本は何ですか？」と聞かれたら、間違いなくこの本を挙げる。

高校 2 年になったぐらいだったか、大学の進路に思い悩んでいたときに 2 つの選択肢を思い悩んでいた。
1 つは考古学、1 つは数学だった。

考古学は、徳川埋蔵金のテレビ特集に夢中になっていた影響もあってか、何かロマンを感じる分野だった。
もう一つは、ただ得意教科だったという理由だけの数学。
中学時代はまったく数学ができなかったが、高校では先生の教え方がうまく、メキメキ数学の成績が上がり最も得意な教科になっていたので、好きと勘違いしていたのだろう。
でも、高校で学ぶ数学と大学で学ぶ数学はまったく違うということも噂で聞いていたので、今数学が得意だから大学も数学科を選ぶという短絡思考もダメだよねぇ・・・と考えていた。

ということで、考古学と数学のどっちが良いかを思い悩んでいたときに、何かのヒントを求めて本屋に立ち寄ったのである。
そのときに出会ったのがこの本だった。

そのときのことはよく覚えていないが、高校数学レベルでも読めそうだというのと、「非」ってどういうこと？と思ったぐらいの印象だったように思う。
この本を買って読み始めると、すごくおもしろくて気が付いたら夢中になっていました。
そして、やっぱり数学っておもしろいっ！！ と思って数学科を目指すことになります。

（ココから先は本のネタバレを含むので、この本を読みたい方は飛ばしてくださいね）

この本は、ユークリッド原論（ユークリッド幾何学）の第 5 公準と呼ばれる「平行線公準」の議論から始まります。
ユークリッド幾何学というのは、中学校・高校で学ぶ一般的な初等幾何学のようなもので、点や線などの基礎的な概念の定義やそれに伴う定理がありますよね。
三角形の内角の和が 180 度になるという、ピタゴラスの定理（三平方の定理）なども有名ですね。
古代エジプト・ギリシャなどで盛んに研究された幾何学を体系的にまとめたものがユークリッド原論と呼ばれているもの。

数学者たちは、このユークリッド原論をバイブルにしてそこに書かれている公準（定理）を証明するのが習わしだったようです。
その多くの公準が書かれたユークリッド原論にある第 5 公準とは以下のようなものでした。

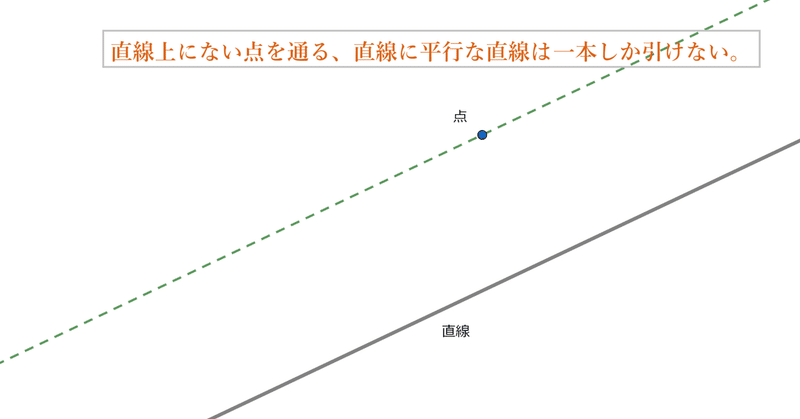
細かい厳密な議論は避けますが、「平行線」というものは以下の公理が成り立っていると思っててください。

そんなの当たり前やん。
線が交わらないから平行というんでしょ？
どう考えてもそりゃ 1 本しか引けんでしょ。

ところが、本を読み進めていくと、この簡単に思える第 5 公準の正しい証明方法を見出すことができず、その議論が 19 世紀まで続くことになります。
その最終的な決着は、第 5 公準の矛盾のない証明方法が発見されたのではありませんでした。

この「平行線」という公理、1 本しか引けないと言っているけど、、、

A) 「直線上にない点を通る、直線に平行な線は 1 本も引けない。」としてみたら？

もしくは

B) 「直線上にない点を通る、直線に平行な線は少なくとも 2 本に引ける。」としてみたら？

そこから、A) の公理が成り立つ矛盾のない理論体系として「楕円（球面）幾何学」という領域が生まれ、B) の公理が成り立つ矛盾のない理論体系として「双曲幾何学」という領域が生まれた・・・だと！？

もう目から鱗がマーライオンみたいに出ましたよ。（笑）

「平面や歪みのない空間」の中でしか物事を捉えていなかったのが、「曲面や歪んだ空間」を持つ新しい世界があるのだと。
衝撃を受けると同時に、何か自分の中での意識のレイヤーが一段上がったような感じでした。

この本の出会いをきっかけにして、大学の進路を「数学科」に完全ロックオンし幾何学を学ぶことを目標にすることとなりました。
そして、数学科に入って「柔らかい幾何学」と呼ばれるトポロジーを学びました。

それから 30 年ほど経った今、なぜこの本はこんなにも自分を揺り動かしたのだろう？・・・と思い返してみました。
数学の美しき世界の一端に触れたからというのもありますが、もっとその奥にある宇宙の真理を感じたから、というのが今になって分かった気がします。

何かしらの定義をすると、その性質が持つ特徴として公理が明確になり、命題や定理が生まれて矛盾のない世界が出来上がっていく。

つまり、人も同じで一つのモノサシ（価値観、倫理観など）を持つことで、その人なりの世界が出来上がる。
人という存在は、そのモノサシによって Create された世界。

世界の総人口が 78 億 7500 万人とされているが、ひとりひとりがモノサシを持って 78 億 7500 万もの世界が広がっている。
他のモノサシがあれば他の世界が存在し、どっちのモノサシが良い・悪い、優れている・劣っているという話ではない。
モノサシの優劣を決めたり、押し付けたりしている間は、非ユークリッド幾何学のような素晴らしい世界は決して Create できないだろう。

ユークリッド原論の第 5 公準の議論から矛盾のない非ユークリッド幾何学成立までに長い年月を要したように、ひとりひとりが Create している世界の中で抱える矛盾について、長い時間をかけて明らかにしていこうとしているように思える。

世界に抱える矛盾を認め、向き合い、議論して、モノサシそのものを再定義する。
どのようなモノサシを持つかで自分の人生（＝世界）が出来上がっていて、それは如何ようにでも自分で Create することができるのだと。

あなたはどんなモノサシを持って世界を Create していますか？