おはようございます。

　読者の皆様に質問です。

　この中で、定規とコンパスのみで作図できるものをすべて選んでください。直感で大丈夫です！！

　この記事では、正$${n}$$角形が作図可能な場合の、面白い定理（数学を使って証明した内容）を紹介します！！

　まず質問の答えを知りたい方は、目次の「答え合わせ」をご覧ください。

１　素数

　この世にある自然数
　１，２，３，４，５，６，７，８，９，・・・
　の中には素数があります。

　素数とは、１とそれ自身の数以外には約数をもたない数です。
　つまり、下の太字の数が素数です。
　１，２，３，４，５，６，７，８，９，・・・

　素数は無限に存在することが紀元前に証明されています。

２　素数の色々な形

　実は、素数は不規則に出現します。
　下の表は、１～１００までの自然数のうち、素数にだけ色をつけたものです。

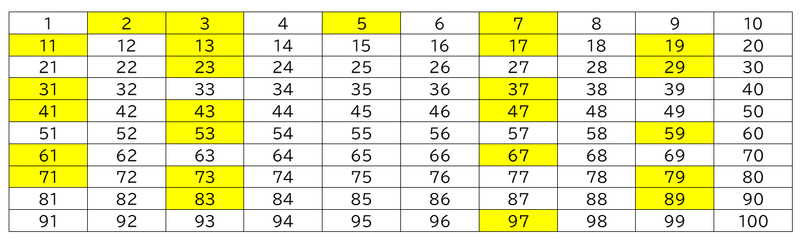
　３，５，７
と１つ飛びで素数が現れることもあれば、

　８９の次は９７
というように７つ飛んでいる場合もあります。

　ですが昔から、人類はどうにかこの不規則な数を作れる計算式はないかと試行錯誤してきました。

　その試行錯誤の１つの成果が「フェルマーの最終定理」で有名な、フェルマーが考えたフェルマー数です。

・　フェルマー数

　フェルマー数$${F_n}$$とは、
　$${F_n=2^{2^n}+1}$$
　で表される数です。

　$${F_0=2^{2^0}+1=2^1+1=3}$$
　$${F_1=2^{2^1}+1=2^2+1=5}$$
　$${F_2=2^{2^2}+1=2^4+1=17}$$
　$${F_3=2^{2^3}+1=2^8+1=257}$$
　$${F_4=2^{2^4}+1=2^{16}+1=65537}$$

　実はこれ、すべて素数です。
　なので、この数を作ったフェルマーは

$${F_n}$$は全て素数である

と予想しました。

　ですが、1732年にレオンハルト・オイラーが$${F_5}$$は素数ではないことを示しました。

$${F_5=2^{2^5}+1}$$
　$${=2^{32}+1}$$
　$${=4294967297}$$
　$${=641×6700417}$$

　ということで、現在知られているフェルマー数のうち、素数になるものをフェルマー素数と呼ぶことにします。
　上で調べたように、$${F_0,F_1,F_2,F_3,F_4}$$がフェルマー素数です。

　現在知られているフェルマー素数で、最大なものは$${F_4=65537}$$です。

３　作図できる図形とフェルマー素数の大事な関係

　当初の疑問「作図できる図形」から脱線しているように思えますが、ここで話を戻します。というか、説明する準備ができました。

　実は、大数学者ガウスがこのようなことを証明しています。

　これだけだと、サンドウィッチマンばりに
「ちょっと何いってるかわかりませ～ん」ですよね（笑）

　具体的に示します。
　２　のところで示したように、

　$${F_0=3}$$
　$${F_1=5}$$
　$${F_2=17}$$
　$${F_3=257}$$
　$${F_4=65537}$$

でした。

　ガウスが発見した定理から、
　正3角形、正5角形、正17角形、正257角形、正65537角形
が作図可能です。
　また、$${n=2^e×F_0×F_1×・・・F_k}$$の$${2^e}$$があるから、
2倍、4倍、8倍、・・・したものも作図可能です。
　（正6角形や正10角形など）

　他にも、同じくガウスの発見した定理から、
　$${3×5=15}$$で、正15角形や
　$${3×5×17=255}$$で、正255角形
も作図可能です。

４　答え合わせ

　では、最初の問いの答え合わせです。

　ガウスの発見した定理から、

５　おわりに

　今回は、正$${n}$$角形の作図可能性と素数の関係について紹介しました。
　いかがだったでしょうか？

　私がこれを見たときは驚きました。

　さらに知識を深めたい方は、ガウスの証明を調べたり、フェルマー数について調べてみてください。面白い性質があります。

　最後に、

　$${3×5×17×257×65537=4294967295}$$
　より、ガウスの定理から
　正4294967295角形の作図ができる！！

ということをお伝えして終わります。

　最後まで読んでいただき、ありがとうございました！