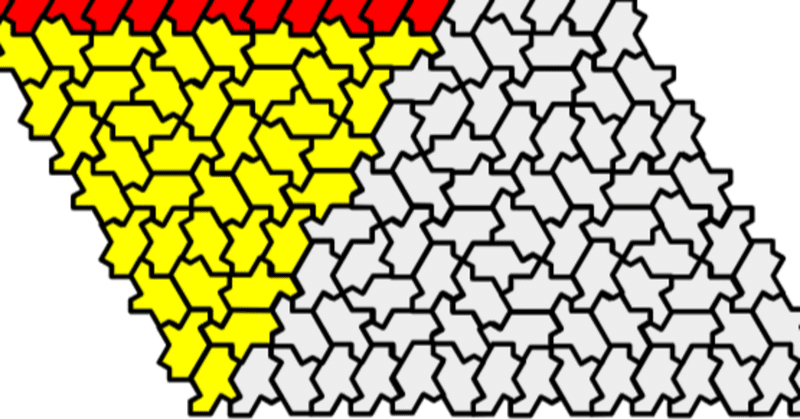
アインシュタインタイルを1列に並べた「GSP」「GSE」を愛でてみる、ようやっと愛でてみる。
前回の記事はこちら。
GSE――Goleden Sturmian Edge――のStumian(スターミアン)のほうが気になって書いたのが前回でした。
ということで、ようやっと愛でます。
GSPのなかにGSEが2つ
前回、GSEを説明する際に図を用いました。
黄色と赤色が1列に並んだ箇所です。
これをGSE、と示したのですがちょっと違ってまして、これはGSP――Golden Sturmian Patch――になります。
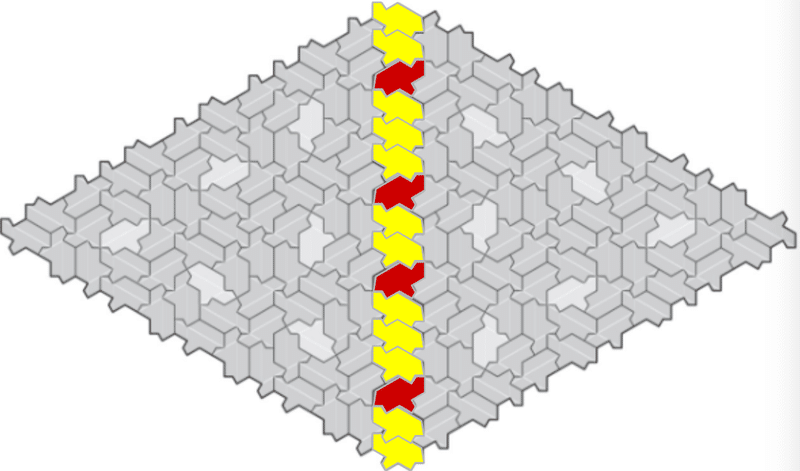
先の図を90度回転してGSEの周辺を切り取ったのが下の図になります。
上(緑線)と下(青線)の2箇所がそれぞれGSEです。

で、これを180度回転します。

なんじゃこりゃ?
タイルはひっくり返っています。
GSEもひっくり返って(色も入れ替わって)いるはずなのに、形状は同じです。
これがGSEの特徴の1つです。
論文「An alternative proof for an aperiodic monotile」の10ページにも、強調した図があります(「Palindrome」は、日本語だと「回文」です)。
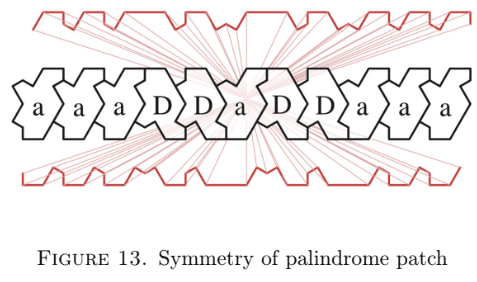
Figure 13
https://arxiv.org/abs/2307.12322
菱形の盤面は省エネ制作?
日本テセレーションデザイン協会代表の荒木義明さんから提供していただいた、アインシュタインタイルマスの2つの盤面があります。
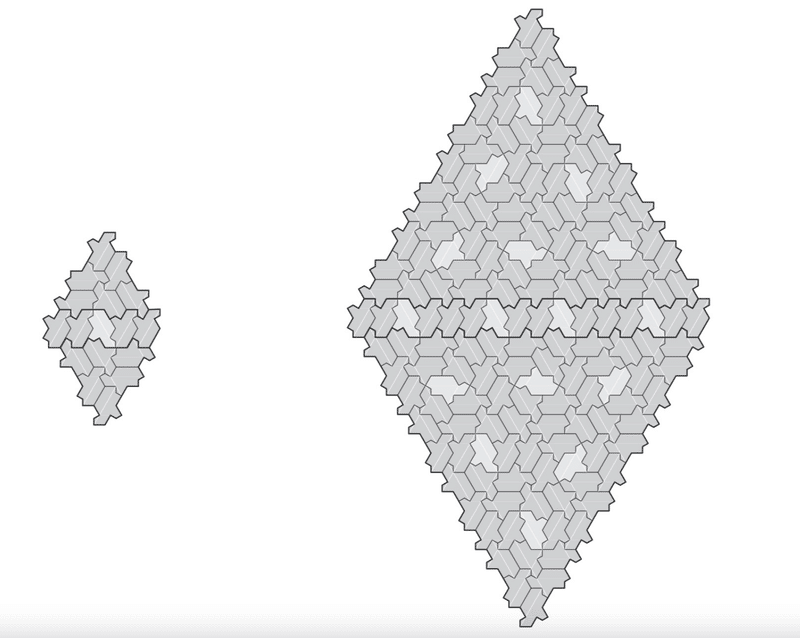
それぞれの盤面の中央を横切るGSPですが、これらはGolden Hex SubstitutionのPD₂とZD₃に含まれています。
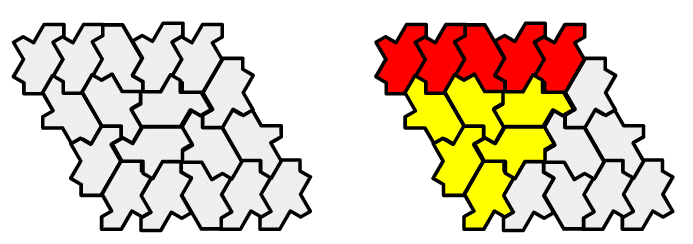
左図がPD₂です。
右図は、赤の部分がGSPで、黄色の部分がT₂です。
GSPの下のGSEにT₂が接しており、GSPの上のGSEに新たなT₂を組み合わせると、4×4の菱形の盤面ができます。
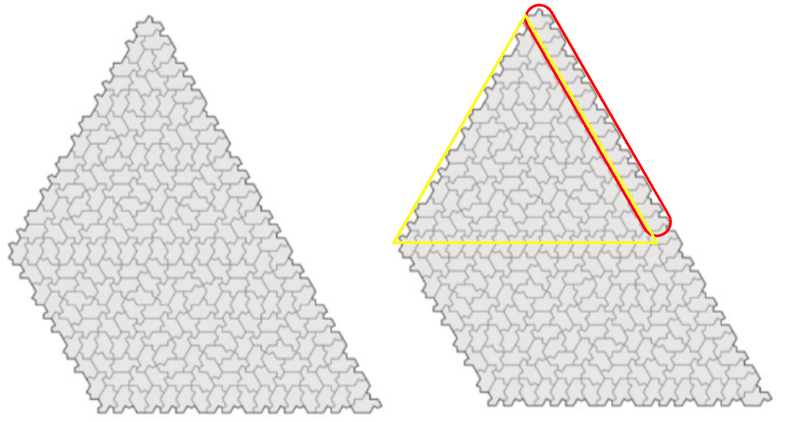
左図がZD₃です。
右図は、赤で囲った箇所がGSPで、黄色の部分がT₃です。
これも同様に新たなT₃を組み合わせると、12×12の菱形の盤面ができます。
これを応用すれば、他(例として、下図はPD₃)から菱形の盤面を作ることもできます。
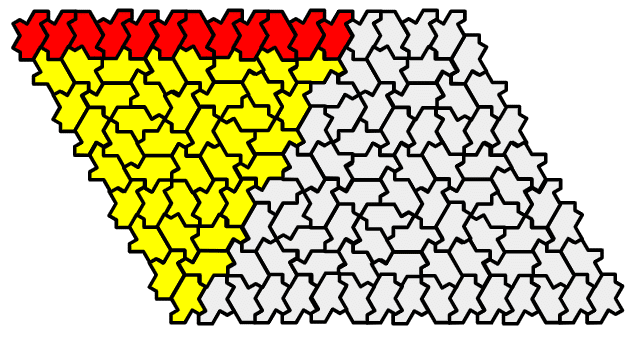
ちなみにGolden Hex SubstitutionのPD、ZD、ZTは、名称にGSEが関わっています。
論文読んで、Golden Hexを愛でていただき有難うございます!
— Yoshiaki Araki 荒木義明 (@alytile) August 15, 2023
パッチタイルには三角形のT(Triangle),平行四辺形に二つGSEがついたPD(Parallelogram with Double GSE),台形に二つGSEがついたZD(trapeZoid with Double GSE),台形に三つGSEがついたZT(trapeZoid with Triple GSE)の四種があります。
パッチタイルには三角形のT(Triangle),平行四辺形に二つGSEがついたPD(Parallelogram with Double GSE),台形に二つGSEがついたZD(trapeZoid with Double GSE),台形に三つGSEがついたZT(trapeZoid with Triple GSE)の四種があります。

Figure 7
https://arxiv.org/abs/2307.12322
※色線は、珍ぬが付け加えました
GSEとスターミアン文字列
GSEは2つの向きのタイルを1列にならべたものです。
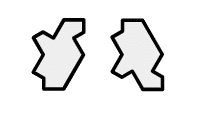
回転して向きが変わっているだけではなく、一方は他方の裏返しになっています。
前回の記事で触れましたSturmian Word(スターミアン文字列)をつかって表すことができます。
論文「An alternative proof for an aperiodic monotile」の9ページにあります。
$${S_0=0,S_1=001,S_n=S_{n-1}S_{n-2}}$$
最初の数項を書き出すと、
第0項 0
第1項 001
第2項 0010
第3項 0010001
第4項 00100010010
第5項 001000100100010001
第6項 00100010010001000100100010010
………
となります。
論文「An alternative proof for an aperiodic monotile」の10ページに、Golden Hex SubstitutionにあらわれるGSPの変遷が図解されています。
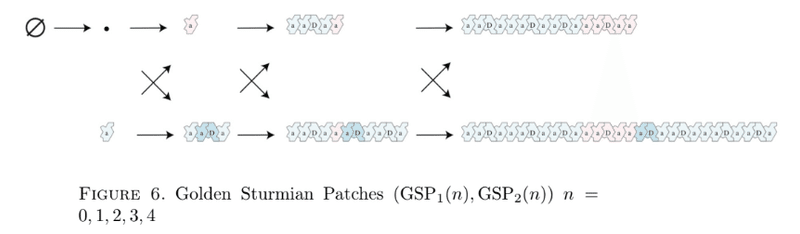
上図では、2つのタイルをaとDで表しています。
aを0、Dを1として置き換えると、

です。
上の段は、奇数番目(1、3、5、……)の項の文字列から右2文字分(01)を除いた文字列が並んでいます。
第1項 001 → 0 (-01)
第3項 0010001 → 00100 (-01)
第5項 001000100100010001 → 0010001001000100 (-01)
そして、それぞれの文字列は回文になっています。
下の段は、偶数番目(0、2、4、6……)の項の文字列が並んでいます。
これも同様に(第0項は例外として、)それぞれの文字列から右2文字分(10)を除くと回文になります。
第0項 0 (例外)
第2項 0010 → 00 (-10)
第4項 00100010010 → 001000100 (-10)
第6項 00100010010001000100100010010 →
001000100100010001001000100 (-10)
前回の記事で触れた、フィボナッチ列(文字列)をビリヤード数列であらわしたような方法で、GSEの値を求めることができます。
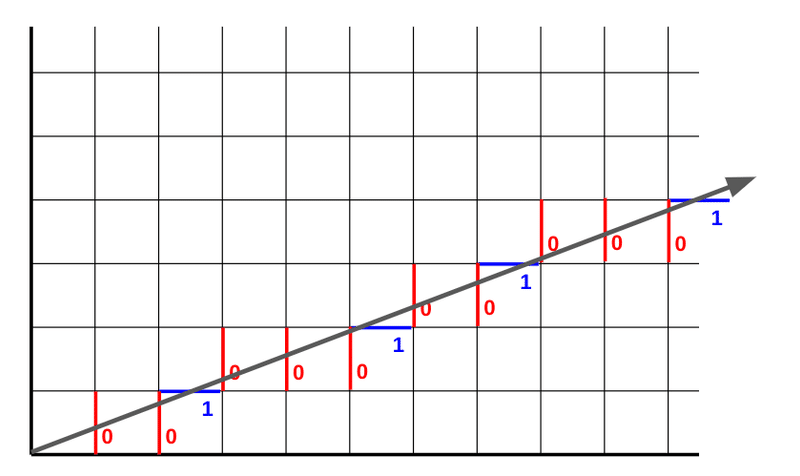
フィボナッチ列は、黄金比から1を引いた数
$${\frac{1+\sqrt{5}}{2}-1 = \frac{1-\sqrt{5}}{2} = 0.618…}$$
でしたが、GSEは論文の10ページをみると、
$${\frac{5-\sqrt{5}}{10} = 0.276……}$$
となります。
ところで、なぜGSEにGolden(黄金)と含まれているかというと、フィボナッチ列の値をGSEにあわせて分母を10にすると、
$${\frac{1-\sqrt{5}}{2} =\frac{5-5\sqrt{5}}{10}}$$
とあらわせるからでは、と思われます。
締めとおまけ
ということで、GSEそしてGSPを愛でてみました。
配置パターンによって敷き詰めが広がっていくと、GSPがどんどん増えていきます。
例えば、ZT₃には下図のように赤および青の点線を引いた箇所がGSPになっています。
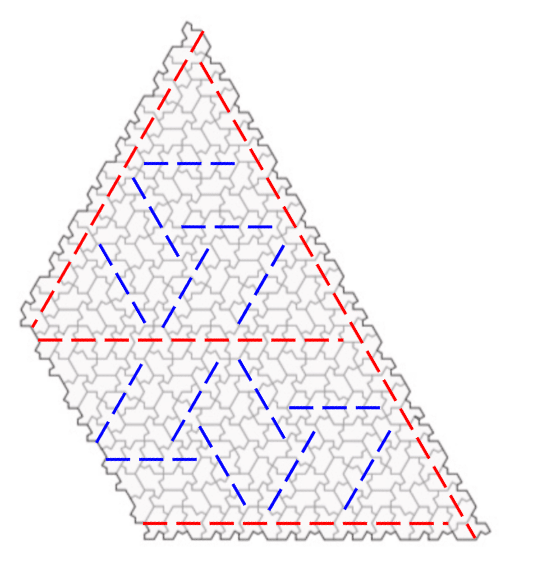
内側には長いGSPが1箇所(赤)と、
短いGSPが14箇所(青)あります。
はい、おまけでした。
次回もよろしくです。
では。
この記事が気に入ったらサポートをしてみませんか?
