前回の記事はこちら。

配置パターンを愛でる予定でしたが、またまた寄り道をします。

展覧会のご紹介

突然ですが。

何度もこの記事のシリーズでお世話になっております「日本テセレーションデザイン協会」。
先週６／１０（土）から、板橋区立教育科学館にて「テセレーション展　かぞくであそぼう！しきつめアート・パズル」が開催中です。

上のイラストの子供たちは、がっつり「HAT」を敷き詰めています。

珍ぬは残念ながら、板橋区へ行くには数百キロの道中＋渡海しなくてはならないので、気軽にいけません。
代わりに行って楽しんでください。

五角形✕５＋三角形✕１

前々回の記事で、こんな図形を描きました。

中央上の図形が、Tile(1,1)です。
その矢印の下の図形は、Tile(1,1)を２つに分割した上部分の図形です。
それを、下部分の図形を半分にした五角形をあてはめています。

じゃあTile(1,1)全体だとどんな感じ？となると……用意していませんでした（今さらで気づきました）。

で、本当にいつもいつもありがとうございますの、日本テセレーションデザイン協会代表・荒木義明さんからのツイートです。

上図の左２つの図形は、Tile(1,1)を（同じ形の五角形５個＋三角形１個に）分割したものになります。

図右上の敷き詰めは、色味と形から「いちご畑」っぽいです。とすると図右上は「杏」っぽい敷き詰め。

それぞれの右側は、論文「A chiral aperiodic monotile」７ページのFigure2.2左上の敷き詰めにあわせています。

David Baileyさんが反応した

で、このツイートの１日前にツイートした人物がおります。David Bailey（デビッド・ベイリー）さんです。

David Baileyさんのサイトはこちら。

Davidさんも、筋金入りのテセレーション愛好家です（TwitterIDも@tessellationfan）。
サイトではいくつかのテーマに沿った記事が書かれていますが、その１つが「Cairo Tiling」で、まさにカイロ五角形がターゲットです。

「HAT」が登場する前、「アインシュタイン問題」に該当する図形は五角形に関係するのでは、と期待されていたとかそうらしかったとか、そんな噂がありました。
そこで「SPECTRES」では五角形が関わっているぞ、となると……喜びたくなる、かも。

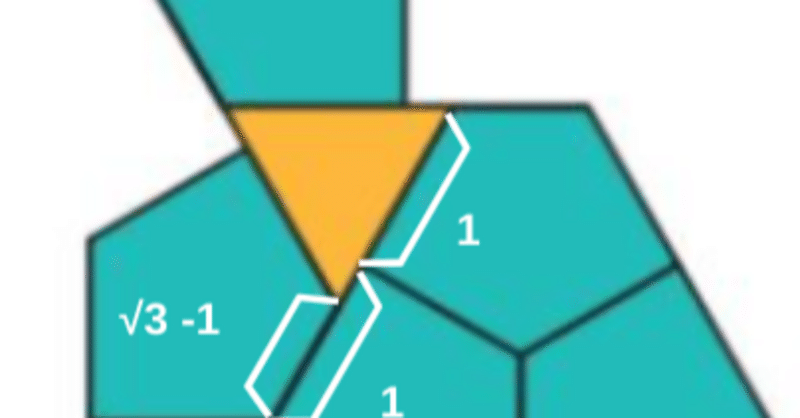
今回のTile(1,1)の分割で使用したカイロ五角形は以下の図形です。

辺の比が１：$${{\sqrt{3}-1}}$$です。
カイロ五角形の４辺を１とすると、Tile(1,1)を分割した残りの三角形（正三角形）の辺は、$${{3-\sqrt{3}}}$$になります。

カイロ五角形のボードゲーム

カイロ五角形を使ったボードゲームだと、２０１３年に発表したNestorGamesの『Cairo Corridor』があります。

和訳すると「カイロ回廊」。
お互いにカイロ五角形タイルを並べて、盤面の４辺がつながるようにタイルが置けなくなるとゲーム終了で、通路に接しているタイルの辺の数が多い方の勝ちとなります。

分割したTile(1,1)を並べた盤面で、遊べるかも……どうなんでしょうか。

自然界に存在する？

自然界には、準結晶構造があります。

ペンローズタイルなど、非周期的敷き詰めのパターンが、準結晶構造にみられるようです。
「HAT」やTile(1,1)、「SPECTRES」のパターンを用いた準結晶構造があるのか、も気になるところです。
今回のカイロ五角形と正三角形の組み合わせを元にした準結晶構造でみることで、発見しやすくなる……かも知れません（と大風呂敷を敷く）。

締め

ということで、今回もまたもや配置パターンを愛で損なっております（といいつつ、ちょっとだけ触れましたが）。

次回、どうするのか。
目下やるやる詐欺中ですが、本当にやるのか。

では。