
アインシュタインタイルを構成する「虚数面積のパーツ(!?)」を愛でてみる。とにかく愛でてみる。
前回の記事はこちら。
HATタイプとSPECTREタイプの敷き詰めで作った盤面でパズルを作ってみました。
で、ちょっと気になったことがあったので、最初の回まで振り返りつつ、つらつら書いていきます。
SPECTREのタイルってどっちに接しているの?
論文「An aperiodic monotile」で登場したHATとのその仲間たち。
そのタイルは、正三角形4個を組み合わせたT₄と正三角形8個を組み合わせたT₈を変形させた中間の形状になります。
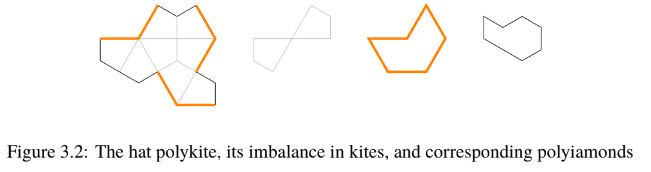
論文18ページの図3.2(上の図)の、右から2番めのオレンジで囲われた図形がT₄で、一番右の図形がT₈です。
なぜ、中間の形状かというと、HATの線分を6つに分けて組み合わせると、
T₄とT₈を作ることができます。

HATを平面に敷き詰めると、2つの異なるタイルの辺が接します。
T₄とT₈の辺の長さは(基本的に)異なるので、あるタイルのT₄に相当する辺は他のタイルのT₄の辺に接し、T₈についてもT₈に接します。
T₄とT₈は長さが異なるので、どうしても隙間が生まれてしまいます。
(基本的に)とカッコ書きしたのは、SPECTREで敷き詰めるTile(1,1)が問題でして、T₄とT₈の辺の長さが同じなのです。
なので、あるタイルのT₄の辺と他のタイルのT₈の辺と接しても、長すぎたり短すぎたりしません。
なにより、HATタイプの敷き詰めでは一部のタイルが裏返しですが、SPECTREタイプの敷き詰めは裏返しなしです。

左図がSPECTREタイプの敷き詰めの配置パターンの1つで、右図がHATタイプの敷き詰めの配置パターンの1つ。
赤のタイルが、HATタイプでは裏返しになっています。
赤のタイル周辺の接し方が気になってくるのです。
ちょっとボリュームをつけてみる
タイルの辺をT₄とT₈とを区別して色分けしてもいいのですが、ちょっと違った表現を思いついてしまいました。
線分のかわりに、T₄やT₈を構成するタイル――正三角形――で組み合わせてはどうかと。
HATの場合、T₈にあたる辺の長さを1とすると、T₄にあたる辺の長さは√3になります。
それらを辺の長さ1の正三角形(赤)と、辺の長さ√3の正三角形(緑)で組み合わせてみると、下の図のようになります。

T₄とT₈の重なっている箇所は青にしてあります。
なんというか……奇妙ではあります。
どう奇妙なのかは、後ほど深掘りします。
で、SPECTREタイプの敷き詰めがどうなっているのかを確認したいので、Tile(1,1)にも適用すると下の図になります。

ということで、敷き詰めてみます。
配置パターンを盤面にして、それより一回り小さめのサイズに縮めて、はめて置くような感じにみせます。
まずは、HATタイプからです。

中央が黄色くなっているタイルは、裏返しのタイルです。
2つのタイルが接している箇所は、赤は赤、緑は緑であわさっています。
では、SPECTREタイプ。
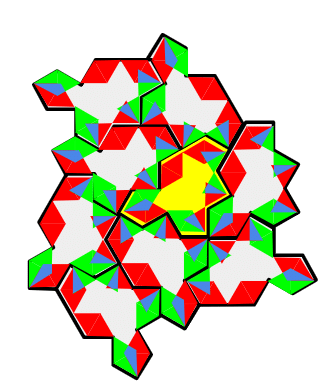
中央が黄色くなっているタイルは、HATタイプだと裏返しになっているものにあたります。
そして、このタイルだけが他のタイルとは、赤に緑、緑に赤と互い違いに合わさっています。
ほかはちゃんと、赤は赤、緑は緑なので、見事に対照的です。
面白い。
で、これからがタイトルの本題になります。
全部正三角形だと困ってしまう
話題は変わります。
後回しにした「奇妙さ」の深堀りです。

T₄とT₈の区別を上のように表現すると、ちょっと噛み合わないところがあるのです。
線分で表現した場合は、それぞれのパーツを組み合わせてT₄とT₈に仕立てることができました。
ただし、正三角形で構成した上の場合だと、
・緑のパーツは6個あって、T₄に仕立てるには2個余分だが重ね合わせることでT₄になる。
・赤のパーツは8個あるが、T₈に仕立てるには1個分のパーツが重なり、1個分不足してしまう。

ということで塩梅がいまひとつです。
さらに、HATの仲間で、T₄とHATの間にある形状――例えばTile(1,3)など――をこの表現であらわすと、下図のようにタイルが一部はみ出します(点線で囲った部分)。

解消できないものか、考えてみます。
ヘリコプターにしてみる(回転主翼)
さて、このシリーズの最初の記事からすでに、HATの仲間のタイルを異なる2つの点対称図形に分割して、ヘリコプターとして愛でてきました。
それぞれを、3つの羽を持つ回転主翼(下図の黄色の部分)、2つの羽を持つ線対称でもある回転尾翼(下図の青色の部分)と呼んで愛でてきました。

では、ヘリコプターを今一度、今回の正三角形奇妙表現で愛でてみます。

回転主翼の形状が、緑の正三角形(T₄)と赤の正三角形(T₈)の大小の変化によって決まることがわかります。
Tile(1,3)も、同様に従います。

回転主翼の行き着くところ、つまりT₄(こと、Tile(0,1))とT₈(こと、Tile(1,0))の回転主翼ですが、どちらも正三角形6個を組み合わせた正六角形1個になります。

ヘリコプターにしてみる(回転尾翼)
次は、回転尾翼です。
そのまま通常の奇妙な表現(これ自体奇妙な文言の表現ですが)であらわすと、下図のようになります。

2箇所あるT₄のパーツは、TURTLE→Tile(1,1)→HATと変化するにつれ、徐々に重なっていきます。
そしてたとえばTile(1,3)になると――見た目には露見しない2個のパーツ(深緑)が――重なりを通り越します。

より一層輪をかけて奇妙なことになってしまいました。
タイルの虚実をひっくり返してみる(回転尾翼)
この際、もっと変なことをしてみますよ(開き直りっ)。
奇妙な表現では、T₄にあたる辺を、正三角形であらわして内部においています。
これを、外部においたらどうなるんだ。
というのが発端です。
一方、T₈に当たる部分。
こちらは大きさは変えずにT₄で重なる部分を削除してみます。
えーと、何を言っているんでしょうかね(笑)。
とりあえず、やってみたいことを図で表してみます。

それぞれの右下が、新しい表現での回転尾翼です。
T₈とT₄のそれぞれの部分は組み合わせると大きさは変わりません。
T₈はT₄の形状にあわせて縮小していきます。
そして今回仕立てたT₄の部分(形状はポリカイト)は、以下の図のような内訳になっています。

そしてT₄の部分ですが、実数ではなく虚数的な扱い――つまり面積が虚数ーーであることにします。
しかも、普通に見えているタイルは実数の面積を持っていて、虚数面積のタイルは、見えません。
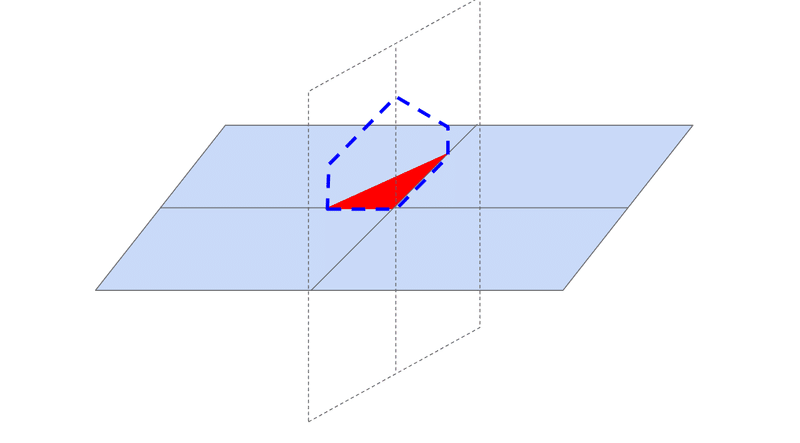
虚数面積のタイル(青)は虚数の面(空間)にあるので見えない。
ますます奇妙なことをして(笑)。
というのも、面積を虚数とすることで、T₄とHATの間にある形状を考える際に、とある都合がつくのです。

右下が、新しい表現での回転尾翼になります。
2つのT₄の部分が重なった部分(白の部分)ですが、
虚数の面積×虚数の面積で、負の面積になります。
余計にますます奇妙なことをして(笑)。
これは以前の記事、

でもふれました、上の図の緑色の部分です。
T₄とHATの間にある形状の回転主翼は、一部が欠けて見えます(黄色の部分)。
しかし、緑色の部分で補うと点対称の図形になります。
つまり、回転尾翼の負の面積が重なることで、回転主翼が点対称でない歪な形状になっていた、ということです。
ありゃま。
ここで照合してしまいました。
さらに突き詰めると、T₄での回転尾翼は、

となります。
負の面積の部分は、正三角形2個分になります。
では、回転主翼と回転尾翼を組み合わせるとどうなるか。

T₄になりました。
まとめて表示
では、2つに分割したアインシュタインタイルの変化を並べてまとめてみます。


中央がアインシュタインタイル。
上が回転主翼で、下が回転尾翼。
締め
ということで、延々と書きました。
異なる2つの図形変換を組み合わせるという、かなり強引なことをしております。
細かいキズやら穴やらたくさんあると思います。
虚数面積のパーツの概念は、ちょっと前から考えていたのですが、書く機会を伺ってようやっと出しました。
いいかげん、せまゲーもやりたいので、次回はそちらの予定です。
では。
この記事が気に入ったらサポートをしてみませんか?
