アインシュタインタイル配置パターン「H7」「H8」を愛でる。とにかく愛でてみる。
前回の記事はこちら。
配置パターンを愛でる予定でしたが、2回ほど寄り道しております。
今回は、いよいよです。
配置パターンとは
タイル敷き詰めの「配置パターン」をおおざっぱに説明すると、
これらのタイルは、
こうしたらうまく敷き詰められますよ、
というルール
です。
このように書くと「非周期的敷き詰めといいつつ、ルールがあるというのは、周期性があるってことで、おかしいじゃないか」と思われる方もいます。
むちゃくちゃ鋭いです。
以前の記事でもリンク先を引用した「周期的タイル張りのみ可能なタイルの話」にある「タイル張りの周期的・周期性・非周期的とは」から、引用します。
一般に,平面の「タイル張りが周期的である(a tiling is periodic)」,つまり「周期的タイル張り(periodic tiling)」とは,ある方向にそのタイル張り全体を平行移動すると自分自身に重なるような方向が2つ存在することを指します(そのように考えている人が多いと思います).これをベクトルという用語を使って言い直すと,タイル張りが2つの一次独立なベクトルによる自身の平行移動したものと一致する場合に該当します.

「敷き詰めたタイル全体を1方向にざっと動かしてみると、動かす前の状態にぴったり一致するようなものが2つ(以上)ある」ということです(左図は一致する方向が2つあるので「周期的」、右図は一致する方向は1つしかないので「非周期的」、とご理解ください、です)。
さらに、「HAT」や「TURTLE」などのタイルが非周期的であることを「非周期的タイル張りのみ可能なタイル「hat」を使った周期性を持つ敷き詰め模様のベルト」にて詳しく考察しております。
まさに、今回愛でるH7、H8は、上のブロク記事で考察していたものです。
H7、H8とは
H7、H8は論文「An aperiodic monotile」の18ページにある、「HAT」などのアインシュタインタイルを複数個(H7は7個、H8は8個)組み合わせたユニットになります。
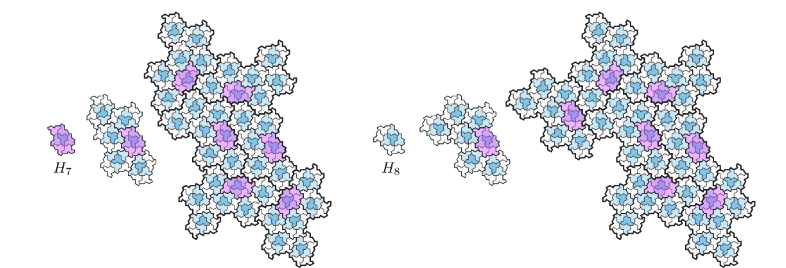
Figure 2.11
https://doi.org/10.48550/arXiv.2303.10798
まず、こちらが「HAT」のH7になります。

真ん中のタイルは唯一裏返しになっています。
そしてこちらが「HAT」のH8になります。

H7の左側に「HAT」(裏返しでない)1個を追加しております。
さて、どのように愛でようかと考えまして、以前の記事でおこなった「回転したもう1つのユニットと重ねてみる」ことにします。
H7を回転して重ねる
やってみると、120度・240度、そして180度がなかなかの重なり具合でした。
まず、120度。

左図は「HAT」のH7。
右図は左図を時計回りに120度回転して、外の輪郭のみを残した図形となります。
では、重ねてみます。

結構重なっていますが、むしろ重なっていない部分が面白い。
左側をみると、まるまる「HAT」1個分重なっていません。
反対に、右側は「HAT」のあの回転主翼1個分が重なっていません。
これらの重なっていない部分は、下側にはみ出しています。
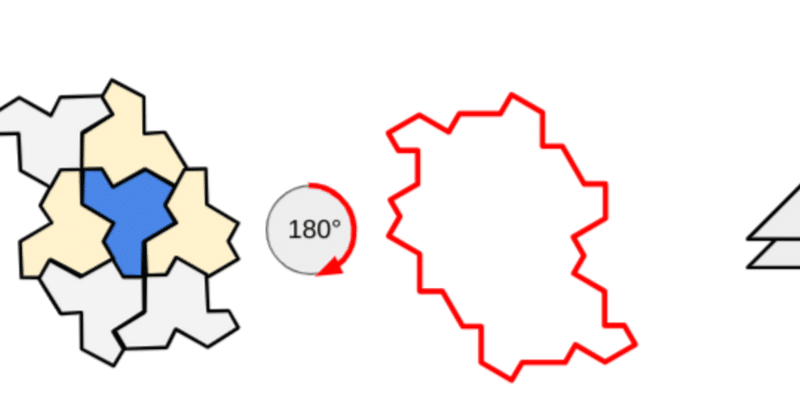
※ 「HAT」は、ヘリコプターのように回転主翼(黄)と回転尾翼(青)の2つの点対称図形に分けることができます。

次に、時計回りに240度回転。

こちらも120度と同じように「HAT」1個分と回転主翼1個分の重なりなしとはみ出しがありますが、反転しています。
さて、180度回転です。
先に言っておくと、なんじゃこりゃ?でした。

120度、240度よりも、重なり度が厚くなっています。
重なっていない回転尾翼1個分が、左右にあります。
……って、この回転尾翼、「HAT」のじゃなくて「TURTLE」のですがな!
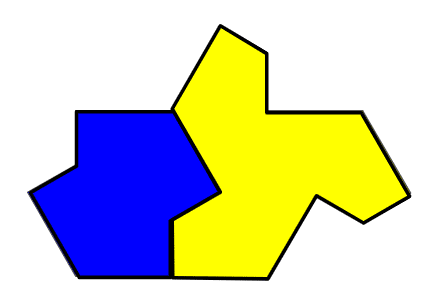
ちょっと待てちょっと待て。
気になったので、「TURTLE」のH7も180回転して重ねてみよう。

今度は、こっちに「HAT」の回転尾翼が登場したではないか。
そうきましたかあ。
H8を回転して重ねる
いろいろ語りたいことはあるのですが、H8も確認してからにします。
まずは「HAT」のH8を120度、そして240度回転して重ねます。

重なっていない部分が、H7よりも固まってスッキリしています。
では、多分問題であろう、180度。

重なっていない部分は、今まで見たことのなかったプロペラ(点対称の図形)です(……というか、H7で重ねたときにもちらっと見えてはいました)。
これって結局、「HAT」に「TURTLE」の回転尾翼を重ねた残りの図形なのです。

右:回転尾翼を「TURTLE」に付け替えた
「HAT」のヘリコプター
そうなると、「TURTLE」に「HAT」の回転尾翼に差し替えてみると、以下の図になります。

右:回転尾翼を「HAT」に付け替えた
「TURTLE」のヘリコプター
「TURTLE」のH8の180度回転重ね合わせをみると、この変形(?)回転主翼が登場しています。

「HAT」「TURTLE」以外も回転して重ねる
さて、そうなると他のアインシュタインタイルのH7、H8はどうなのか。
以前の記事で書いたTile($${{3\sqrt{3},1}}$$)(左図)とTile($${{1,3\sqrt{3}}}$$)(右図)だと、どうなのか。

凧形を複数枚組み合わせた
形状のアインシュタインタイル。
それぞれのタイルのH7は、下の図。

このように並べてみると、同じ系列の図形とは思えませんね。
まずは、Tile($${{3\sqrt{3},1}}$$)のH7を180度回転して重ねます。

重ならない部分は、Tile($${{1,3\sqrt{3}}}$$)の回転尾翼になります。
「HAT」「TURTLE」のペアと同じく、Tile($${{3\sqrt{3},1}}$$)にTile($${{1,3\sqrt{3}}}$$)の回転尾翼(青)が重なります。

次は、Tile($${{1,3\sqrt{3}}}$$)のH7を180度回転して重ねます。

以前の記事を読まれた方は「ああ、そうだった」と思い出したかも知れません。
他のタイルと違い、3つの図形に分かれています……が、どういうことなの?
せっかくなので、H8を180度回転して重ねてみます。

こちらだと、変形した後の回転主翼の形が見えています。
Tile($${{1,3\sqrt{3}}}$$)にTile($${{3\sqrt{3},1}}$$)の回転尾翼(青)が重なると、下図になります。
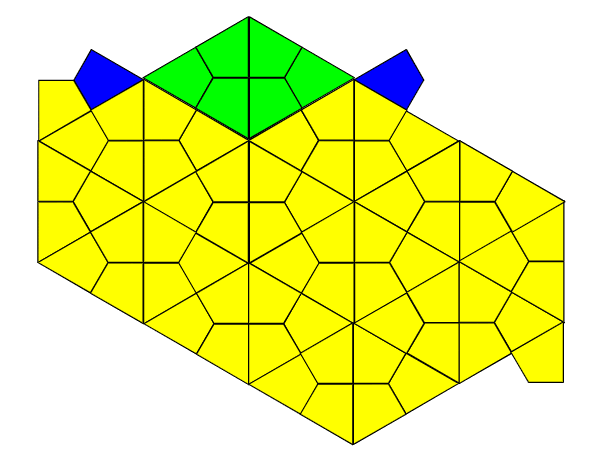
謎の図形が出現した
ヘリコプター
H7の3つの図形は、回転尾翼(青)と新しく出現した図形(緑)です。
左右それぞれに分かれてはみ出したり重ならなかったりします。
H8で、はみ出したり重ならなかったりする回転主翼は、黄色と緑の図形の組み合わせになります。

青・緑・黃の図形の関与が
みてとれるのでは?
締め
ということで時代に逆らい、前の論文の配置パターンを愛でてみました。
Tile(1,1)に全く触れていませんが、もうすでにお腹いっぱいです。
ということで、次回はやり残したTile(1,1)での配置パターンの回転重ね合わせです。
では。
この記事が気に入ったらサポートをしてみませんか?
