この記事は、テキスト「たのしいベイズモデリング」の第19章「男女間のナルシシズム傾向の差の検討」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

この章では、ナルシシズム～自己愛性の傾向について、項目反応モデルを適用したベイズモデリングで推論します。
項目反応理論は学術的に確立された「テストの得点」に関わる理論です。

推論の結果を用いて美麗な曲線グラフを描きます。
さあ一緒に、PyMCのベイズモデリングの最終回の旅へ出発です！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　北條大樹 先生
モデル難易度：　★★・・・　（やさしめ）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★・・& そこそこ \\
結果再現度 & ★★★・・& そこそこ \\
楽しさ & ★★★★★& 楽しい！ \\
\end{array}
$$

評価ポイント

• ２つのモデルは収束しました。
  ただし、テキストの結果と相違がいくつか見られました。
  最終回なのでしっかり結果を出したかったのですが・・・
  キーーー（叫び）

工夫・喜び・反省

• １周目では１つ目のモデルの項目特性曲線をうまく描画できませんでした。
  ブログ原稿を書くにあたって、再度コードを確認したところ、横軸の値がRスクリプトと異なっていたり（描画に用いる$${\theta}$$の取得方法）、計算に用いる変数を間違えていたり（$${\alpha}$$と$${\beta}$$の取り違い）と、苦い発見がありました。
  コード自己チェックの大切さを改めて噛み締めました。

モデルの概要

テキストの調査・実験の概要

■ 分析目的
著者によると分析目的は、ナルシシズムを測定する尺度を用いて、男女間のナルシシズムの捉え方の違いをベイズモデリングで分析して、「結果をもとに” ちょいナル男 ”になるためにどうすればよいのかを検討する」ことです。

■ データの概要
一般人のナルシシズムの程度を測定するための「自己愛性人各尺度：NPI尺度」の公開データセットを利用します。
11243人が40の質問に回答した「NPI尺度の項目回答データ」です。
次のサイトの「Updated: 9/6/2012」のデータです。

■ 項目反応モデル
テキストによると、項目反応モデルは項目反応理論（Item Response Theory）と呼ばれるテスト理論に依拠した確率モデルです。
回答者の回答（項目反応、0または1）$${y_{ij}}$$を「回答者$${j}$$に関する潜在変数$${\theta_j}$$」と「質問項目に関する潜在変数$${\alpha_i,\ \beta_i}$$」で表現するモデルです。

テキストの図19.1のプレート表現をお借りして図示します。

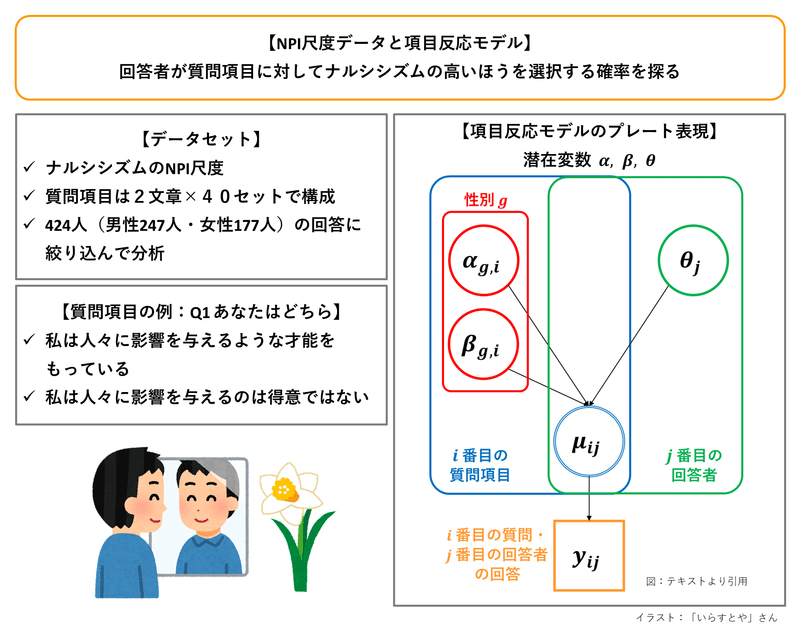
テキストのモデリング

■目的変数と関心のあるパラメータ
目的変数は、回答$${y_{ij}}$$です。
関心のあるパラメータは項目反応モデルの３つの潜在変数です。
・$${\theta_j}$$：回答者$${j}$$の特性値（能力とも呼ばれる）
・$${\alpha_i}$$：質問項目$${i}$$の識別力
・$${\beta_i}$$：質問項目$${i}$$の困難度

■ モデル数式
項目反応モデルに従っています。

性別効果検討のための拡張項目反応モデルでは、性別の属性$${g}$$を加えることとされ、$${\alpha_{g,i},\ \beta_{g,i}}$$となります。

次の上の式はロジスティック関数のことであり、下の式で書き換え可能です。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# PyMC
import pymc as pm
import arviz as az

# 描画
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．データの読み込みと前処理
あらかじめテキスト掲載サイトから zip ファイルをダウンロードして、data.csv ファイルを解凍しておきます。
解凍した csv ファイルを pandasのデータフレームに読み込みます。

### データの読み込み

# データ取得先URL
# http://openpsychometrics.org/_rawdata/NPI.zip

# データの読み込み
data_orgn = pd.read_csv('data.csv')

# データの表示
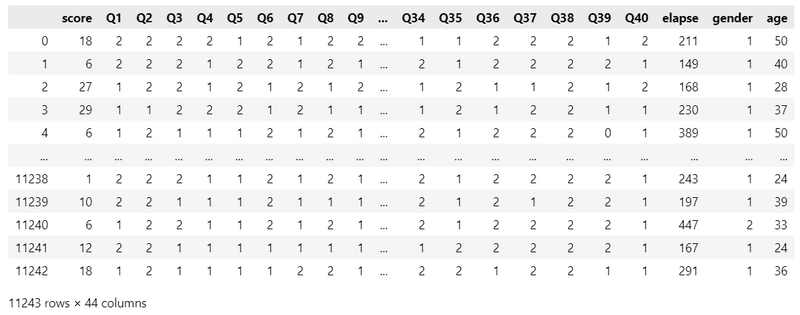
display(data_orgn)

【実行結果】
全11243行（11243人）、40設問のデータです。

続いてデータの前処理を行います。
Rスクリプトと同様のデータ絞り込み・欠損値処理・逆転項目の対処を施した後に、データを縦持ちにしてPyMCモデルで扱いやすくします。

### データの前処理

### データの絞込み、欠損値の削除、値の変更（0始まりへ）
# 年齢=20歳に絞り込む
data = data_orgn[data_orgn['age']==20]
# 欠損値処理：Q1～Q40の値0の行を削除する
for col in data.columns[1:41]:
    data = data[data[col]!=0]
# 欠損値処理：genderの値0, 3の行を削除する
data = data[data['gender'].isin([1, 2])]
# 列の削除: score, elapse, age
data = data.drop(columns=['score', 'elapse', 'age'])
# 値を0始まりに変更する
data = data - 1
# 回答選択肢が逆転している項目について0と1を反転（Rコードと同じ処理）
data[['Q4','Q5','Q7','Q9','Q10','Q15','Q17','Q18','Q19','Q20','Q22',
      'Q23','Q26','Q28','Q32','Q35','Q40']] \
    = 1 - data[['Q4','Q5','Q7','Q9','Q10','Q15','Q17','Q18','Q19','Q20','Q22',
                'Q23','Q26','Q28','Q32','Q35','Q40']]

# インデックスのリセット
data.reset_index(drop=True, inplace=True)
data.reset_index(drop=False, inplace=True)

### 回答を縦持ちに変換
# 回答を縦持ちに変換
data = data.melt(id_vars=['index', 'gender'], value_vars=data.columns[1:42])
# 列名の変更
data.columns = ['id', 'gender', 'QNo', 'answer']
# QNoの値の変更：Qの文字の削除と0始まりへ変更
data['QNo'] = data['QNo'].apply(lambda x: int(x[1:])-1)
# 並び替え（id, QNoの昇順ソート）
data.sort_values(by=['id', 'QNo'], inplace=True)
data.reset_index(drop=True, inplace=True)

### 前処理後のデータの表示
display(data)

【実行結果】
項目の内容は次のとおりです。
・id：回答者のID（0始まり）
・gender：性別、0：男性、1女性
・QNo：質問項目の番号（0始まり）
・answer：回答、1がナルシシズムの高さを示す

３．データの外観の確認
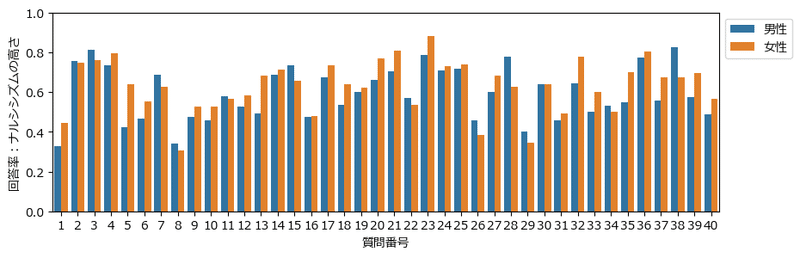
性別ごとに各質問項目の回答率（ナルシシズムの高さ）を描画します。

### ナルシシズムの高さの棒グラフ（性別）の描画

## データの整形
# 質問番号別・男女別の回答率を算出
plot_data = data.groupby(['QNo', 'gender'])['answer'].mean().reset_index()
# genderの項目値の変換
plot_data['gender'] = plot_data['gender'].replace([0, 1], ['男性', '女性'])

## 描画
plt.figure(figsize=(10, 3))
# 男女別の棒グラフの描画
sns.barplot(data=plot_data, x=plot_data['QNo']+1, y='answer', hue='gender')
# 修飾
plt.xlabel('質問番号')
plt.ylabel('回答率：ナルシシズムの高さ')
plt.ylim(0, 1)
plt.legend(bbox_to_anchor=(1, 1));

【実行結果】
青が男性、オレンジが女性です。
質問によって、ナルシシズムの高さの性別差があるように見えます。

モデル化の前に項目特性曲線の形状を確認します。
テキストの図19.2に相当する図です。

### 項目特性曲線の描画 ※図19.2に相当

# ロジスティック関数の定義
def logistic(alpha, beta, theta):
    return 1 / (1 + np.exp(-(alpha * (theta - beta))))

# thetaの範囲と描画点を取得
theta = np.linspace(-4, 4, 201)

# 描画
plt.figure(figsize=(7, 3))
plt.plot(theta, logistic(1, 0, theta), label=r'Q1: $\alpha_i$=1, $\beta_i$=0')
plt.plot(theta, logistic(3, 0, theta), label=r'Q2: $\alpha_i$=3, $\beta_i$=0')
plt.plot(theta, logistic(3, 1, theta), label=r'Q3: $\alpha_i$=3, $\beta_i$=1')
plt.xlabel(r'特性値 $\theta$')
plt.ylabel(r'反応確率 $\mu$')
plt.legend();

【実行結果】

【読み解き：識別力$${\alpha_i}$$と困難度$${\beta_i}$$】
Q1とQ2は$${\alpha_i}$$：項目の識別力の値が異なります。
値が大きいほど０付近の勾配が急になっています。
Q2とQ3は$${\beta_i}$$：項目の困難度の値が異なります。
値が大きいほどグラフは右にシフトしていて、個人の特性値$${\theta}$$が高くないと反応確率も高くならない傾向が分かります。

通常の項目反応モデルの構築

２つのモデルに取り組みます。
こちらは性別効果を考慮しない「通常の項目反応モデル」です。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\alpha_i &\sim \text{logNormal}\ (\text{mu}=0,\ \text{sigma}=0.25) \\
\beta_i &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=5) \\
\theta_j &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1) \\
\mu_{ij} &= \cfrac{1}{1+\exp(-(\alpha_i (\theta_{j-\beta_i})))} \\
likelihood &\sim \text{Bernoulli}\ (\text{p}=\mu_{ij}) \\
\end{align*}
$$

１．モデルの定義
数式表現を実直にモデル記述します。

### モデルの定義

# インデックスの取得
idx_id = data['id'].values
idx_qno = data['QNo'].values

# モデルの定義
with pm.Model() as model1:
    
    ### データ関連定義
    # coordの定義
    model1.add_coord('data', values=data.index, mutable=True)
    model1.add_coord('id', values=list(set(data['id'])), mutable=True)
    model1.add_coord('question', values=data_orgn.columns[1:41],
                     mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=data['answer'], dims='data')
    idIdx = pm.ConstantData('idIdx', value=idx_id, dims='data')
    qnoIdx = pm.ConstantData('qnoIdx', value=idx_qno, dims='data')
    
    ### 事前分布
    # 項目の識別力
    alpha = pm.LogNormal('alpha', mu=0, sigma=0.25, dims='question')
    # 項目の困難度
    beta = pm.Normal('beta', mu=0, sigma=5, dims='question')
    # 個人の特性値（能力）
    theta = pm.Normal('theta', mu=0, sigma=1, dims='id')
    
    # muの計算
    mu = pm.Deterministic('mu',
              pm.invlogit(alpha[qnoIdx] * (theta[idIdx] - beta[qnoIdx])),
              dims='data')
    # （参考）Bernoulli分布のlogit_p引数を利用する場合
    # logitP = pm.Deterministic('logitP',
    #                     alpha[idx_qno] * (theta[idIdx] - beta[idx_qno]),
    #                     dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=mu, observed=y, dims='data')
    # （参考）Bernoulli分布のlogit_p引数を利用する場合
    # likelihood = pm.Bernoulli('likelihood', logit_p=logitP, observed=y,
    #                           dims='data')

【モデル注釈】

• coordの定義
  座標に名前を付けたり、その座標が取りうる値を設定できます。
  今回は次の３つを設定しました。
  ・データの座標：名前「data」、値「dataのindex」
  ・回答者IDの座標：名前「id」、値「id」
  ・質問IDの座標：名前「question」、値「質問番号」

• dataの定義
  目的変数である回答$${y}$$、回答者IDのインデックス$${idIdx}$$、質問IDのインデックス$${qnoIdx}$$です。

• パラメータの事前分布
  パラメータ$${alpha, beta, theta}$$はテキスト指定の分布、パラメータを用いました。

• muの計算
  ロジスティック関数でパラメータ$${alpha, beta, theta}$$の演算を行っています。

• 尤度
  ベルヌーイ分布です。

２．モデルの外観の確認

# モデルの表示
model1

【実行結果】
シンプルな構成です。

# モデルの可視化
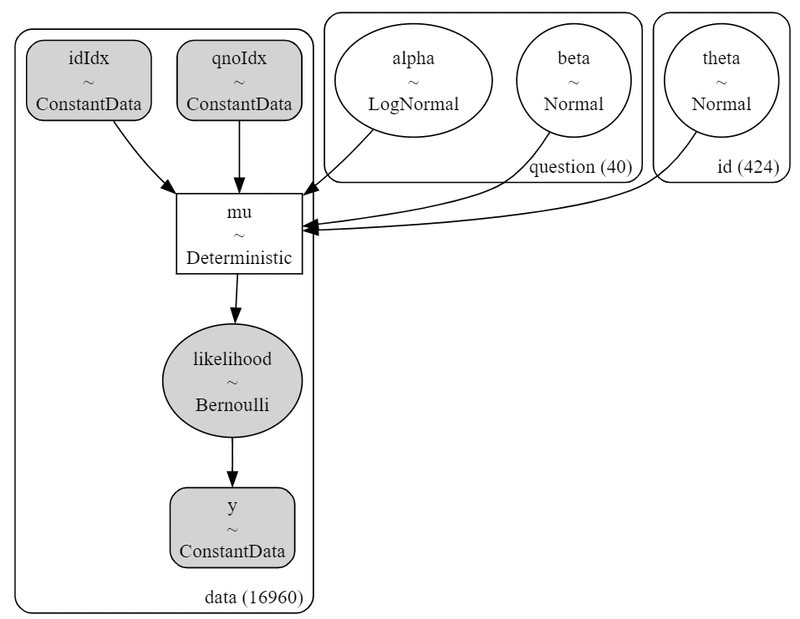
pm.model_to_graphviz(model1)

【実行結果】
パラメータ$${alpha, beta}$$は質問項目数$${40}$$、$${theta}$$は回答者数$${424}$$です。
観測データと反応確率$${mu}$$は$${16960}$$あります。

３．事後分布からのサンプリング
乱数生成数のうち tune（バーンイン期間）はテキストよりも多めにしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ7分40秒でした。

### 事後分布からのサンプリング numpyro 7分40秒
# テキスト：draws=5000, tune=500, chains=4, thin=10
with model1:
    idata1 = pm.sample(draws=5000, tune=5000, chains=4, target_accept=0.9,
                       nuts_sampler='numpyro', random_seed=1234)

【実行結果】（一部）

４．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat>1.1の確認
rhat_idata1 = az.rhat(idata1)
(rhat_idata1 > 1.1).sum()

【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示 7分50秒
pm.summary(idata1, hdi_prob=0.95).round(3)

【実行結果】

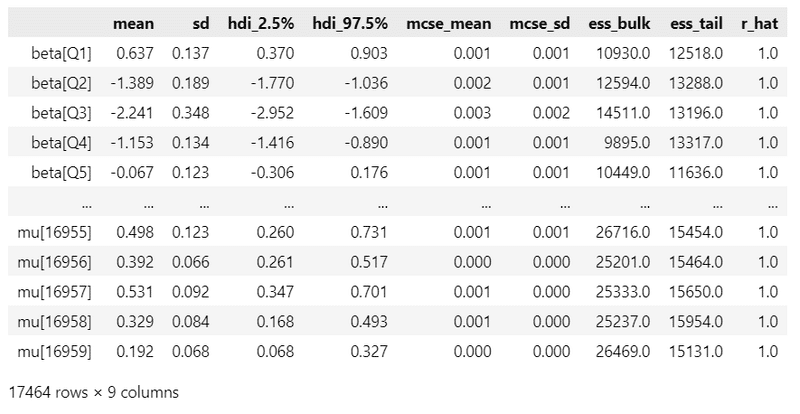
トレースプロットで主要パラメータの事後分布サンプリングデータの様子を確認します。

### トレースプロットの描画
var_names = ['alpha', 'beta', 'theta']
pm.plot_trace(idata1, compact=True, var_names=var_names)
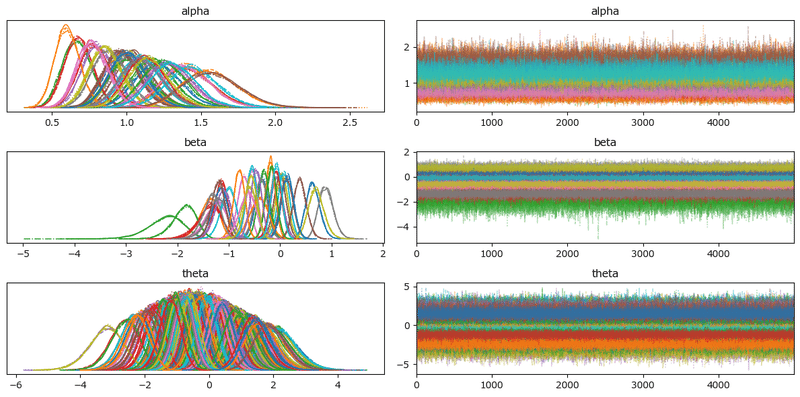
plt.tight_layout();

【実行結果】
収束している感じがします。

５．分析
パラメータ推定値の平均を用いて、項目特性曲線を描画します。
テキストの図19.3に相当します。
matplotlib.cm の cm で春・冬のカラーマップを利用しました。

### 事後平均値をもとに描いた項目特性曲線 ※図19.3に対応

# ロジスティック関数の定義
def logistic(alpha, beta, theta):
    return 1 / (1 + np.exp(-(alpha * (theta - beta))))

# α, βの平均値の算出
alpha_mean = idata1.posterior.alpha.data.reshape(20000, 40).mean(axis=0)
beta_mean = idata1.posterior.beta.data.reshape(20000, 40).mean(axis=0)
# thetaの範囲と描画点を取得
theta = np.linspace(-4, 4, 201)

# 反応確率の算出
res_prob = []
for i in range(40):
    res = logistic(alpha_mean[i], beta_mean[i], theta)
    res_prob.append(res)

# 描画
plt.figure(figsize=(8, 4))
# 0.5の水平点線の描画
plt.axhline(0.5, color='black', lw=0.5, ls='--')
# 0の垂直点線の描画
plt.axvline(0, color='black', lw=0.5, ls='--')
# 40問の反応確率の描画
for i in range(40):
    if i in [2, 22]:           # 困難度の特に低い２項目
        plt.plot(theta, res_prob[i], alpha=1, ls='--', label=f'質問{i+1}',
                 color=cm.spring(i/40))
    elif i in [7, 28, 0, 25]:  # 困難度の特に高い４項目
        plt.plot(theta, res_prob[i], alpha=1, ls=':', label=f'質問{i+1}',
                 color=cm.winter(i/40))
    else:
        plt.plot(theta, res_prob[i], alpha=0.5, lw=0.8, color=cm.tab20c(i/40))
# 修飾
plt.xlim(-4.2, 4.2)
plt.yticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel('特性値 $\\theta$')
plt.ylabel('反応確率 $\\mu$')
plt.legend()
plt.show()

【実行結果】
テキストの結果に近いと思います！

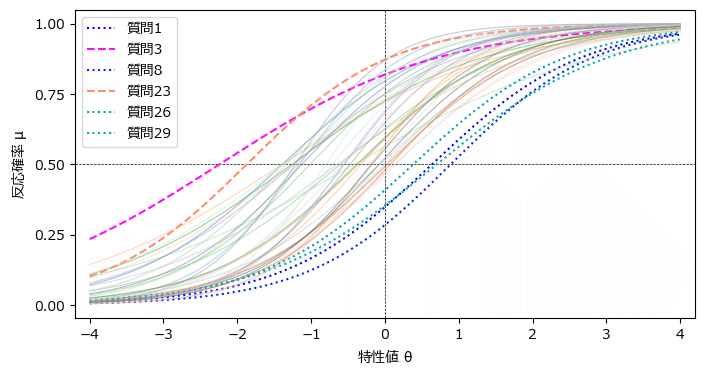
【読み解き】
上側に位置する太点線の質問３と２３は困難度$${\beta_i}$$が低く、下側に位置する細点線の質問１、８、２６、２９は困難度$${\beta_i}$$が高い結果となりました。
困難度が低い質問項目は、ナルシシズム傾向が高くなくても、ナルシシズム側の回答が選ばれやすい項目です。
一方で、困難度が高い質問項目は、ナルシシズム傾向が高くないとナルシシズム側の回答が選ばれにくい項目ですので、質問１，８，２６，２９の値が「１」の回答者はナルシシズム度が高い人という見方ができます。

６．推論データ（idata）の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle
file = r'idata1_ch19.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata1, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata1_ch19.pkl'
with open(file, 'rb') as f:
    idata1_load = pickle.load(f)

拡張項目反応モデルの構築

こちらのモデルでは性別効果を検討するため、パラメータに性別の属性$${g}$$を加えて、$${\alpha_{g,i},\ \beta_{g,i}}$$とするモデルです。

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\alpha_{g,i} &\sim \text{logNormal}\ (\text{mu}=0,\ \text{sigma}=0.25) \\
\beta_{g,i} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=5) \\
\theta_j &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1) \\
\mu_{ij} &= \cfrac{1}{1+\exp(-(\alpha_i (\theta_{j-\beta_i})))} \\
likelihood &\sim \text{Bernoulli}\ (\text{p}=\mu_{ij}) \\
\end{align*}
$$

１．モデルの定義
数式表現を実直にモデル記述します。

### モデルの定義

# インデックスの取得
idx_id = data['id'].values
idx_qno = data['QNo'].values
idx_gnd = data['gender'].values

# モデルの定義
with pm.Model() as model2:
    
    ### データ関連定義
    # coordの定義
    model2.add_coord('data', values=data.index, mutable=True)
    model2.add_coord('id', values=list(set(data['id'])), mutable=True)
    model2.add_coord('gender', values=list(['男性','女性']), mutable=True)
    model2.add_coord('question', values=data_orgn.columns[1:41],
                     mutable=True)
    
    # dataの定義
    y = pm.ConstantData('y', value=data['answer'], dims='data')
    idIdx = pm.ConstantData('idIdx', value=idx_id, dims='data')
    gndIdx = pm.ConstantData('gndIdx', value=idx_gnd, dims='data')
    qnoIdx = pm.ConstantData('qnoIdx', value=idx_qno, dims='data')
    
    ### 事前分布
    # 項目の識別力
    alpha = pm.LogNormal('alpha', mu=0, sigma=0.25, dims=('gender', 'question'))
    # 項目の困難度
    beta = pm.Normal('beta', mu=0, sigma=5, dims=('gender', 'question'))
    # 個人の特性値（能力）
    theta = pm.Normal('theta', mu=0, sigma=1, dims='id')
    
    # muの計算
    mu = pm.Deterministic('mu',
              pm.invlogit(alpha[gndIdx, qnoIdx]
                          * (theta[idIdx] - beta[gndIdx, qnoIdx])),
              dims='data')
    
    ### 尤度
    likelihood = pm.Bernoulli('likelihood', p=mu, observed=y, dims='data')

【モデル注釈】
通常の項目反応モデルとの相違点です。

• coordの定義
  性別の座標「gender」を追加しました。値は [ 男性, 女性 ] です。

• dataの定義
  性別のインデックス$${gndIdx}$$を追加しました。

• パラメータの事前分布
  パラメータ$${alpha, beta}$$の次元（dims）を [ 性別, 質問番号 ] に変更しました。

• muの計算
  パラメータ$${alpha, beta}$$を二次元に変更しました。

２．モデルの外観の確認

# モデルの表示
model2

【実行結果】
シンプルな構成です。

# モデルの可視化
pm.model_to_graphviz(model2)

【実行結果】
$${gndIdx}$$が追加され、パラメータ$${alpha, beta}$$の次元が変わりました。

３．事後分布からのサンプリング
乱数生成数のうち tune（バーンイン期間）はテキストよりも多めにしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ9分20秒でした。

### 事後分布からのサンプリング 9分20秒
with model2:
    idata2 = pm.sample(draws=5000, tune=5000, chains=4, target_accept=0.9,
                       nuts_sampler='numpyro', random_seed=1234)

【実行結果】（一部）

４．サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。

### r_hat<1.1の確認 4分
rhat_idata2 = az.rhat(idata2)
(rhat_idata2 > 1.1).sum()

【実行結果】
$${\hat{R} > 1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示 9分
pm.summary(idata2, hdi_prob=0.95).round(3)

【実行結果】

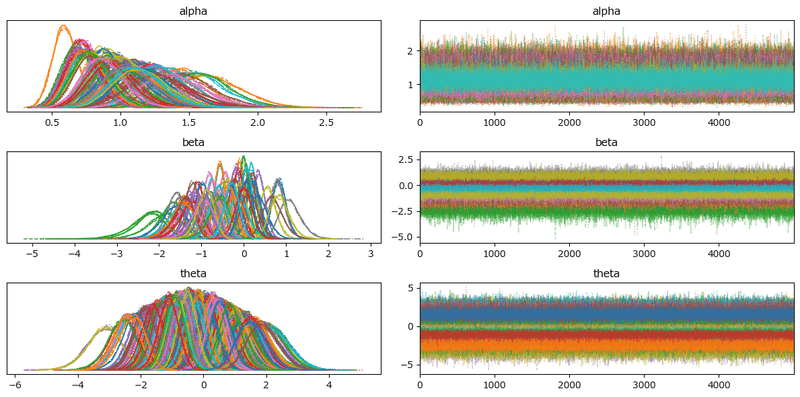
トレースプロットで主要パラメータの事後分布サンプリングデータの様子を確認します。

### トレースプロットの描画
var_names = ['alpha', 'beta', 'theta']
pm.plot_trace(idata2, compact=True, var_names=var_names)
plt.tight_layout();

【実行結果】
収束している感じがします。

５．分析
パラメータ推定値の平均を用いて、項目特性曲線を描画します。
テキストの図19.4に相当します。

### 図19.4の描画のための各種値の算出

# ロジスティック関数の定義
def logistic(alpha, beta, theta):
    return 1 / (1 + np.exp(-(alpha * (theta - beta))))

# α, βの平均値の算出
alpha_mean = idata2.posterior.alpha.mean(dim=('chain', 'draw')).data
beta_mean = idata2.posterior.beta.mean(dim=('chain', 'draw')).data
# thetaの範囲と描画点を取得
theta = np.linspace(-4, 4, 201)

# 反応確率 logistic(α(θ-β))の算出
res_prob_male = []                        # 男性の反応確率を格納するリスト
res_prob_female = []                      # 女性の反応確率を格納するリスト
for i in range(40):
    # 男性の反応確率を算出してリストに格納
    res = logistic(alpha_mean[0, i], beta_mean[0, i], theta)
    res_prob_male.append(res)
    # 女性の反応確率を算出してリストに格納
    res = logistic(alpha_mean[1, i], beta_mean[1, i], theta)
    res_prob_female.append(res)

【実行結果】なし

描画します。

### 男女差の大きかった項目の項目特性曲線の描画 ※図19.4に対応

# グラフに表示する質問文章
q_list = [
    '私の身体に特別なところは無い\n私は自分の体を見るのが好きだ',
    '私がもっと有能だったら決断における責任を担いたい\n決断における責任を担うのが好きだ',
    '生まれつきリーダーとしての素質がある\nリーダーシップを取るには長い時間がかかるだろう',
    '時々、私は良いことをいう\n誰もが私の話を聞くのが好きだ',
    '私は積極的である\n私はもっと積極的だったらいいのに',
    'ほどよく幸せになりたい\n目に見えるものなんでもほしい']

# 描画
plt.figure(figsize=(8, 12))
# リストの質問番号の項目特性曲線を描画
for i, q in enumerate([19, 17, 36, 23, 11, 18]):
    plt.subplot(3, 2, i+1)
    # 男性の曲線の描画
    plt.plot(theta, res_prob_male[q-1], color='steelblue', label='男性')
    # 女性の曲線の描画
    plt.plot(theta, res_prob_female[q-1], color='tomato', ls='--',
             label='女性')
    # 修飾（axes単位）
    plt.xlim(-4.2, 4.2)
    plt.title(f'Q{q}:{q_list[i]}', fontsize=10)
    plt.xlabel(r'特性値 $\theta$')
    plt.ylabel(r'反応確率 $\mu$')
    plt.legend()
# 修飾（グラフ全体）
plt.suptitle('男女差の大きかった項目の項目特性曲線', fontsize=16)
plt.tight_layout()
plt.show()

【実行結果】
Q36、23、18はテキストの結果に近いと思います。
しかし、Q19、17、11はテキストの結果とかけ離れました。
最後のコードで微妙な状況になりました（汗）

【読み解き】
青実線が男性、オレンジ点線が女性です。
線が上側（左側）に位置する場合、がナルシシズム傾向の回答をしやすい質問項目です。
上記の図に当てはめると、Q18と23は女性がナルシシズム傾向の回答をしやすいと言えそうです。
Q36は特性値が低いと女性の方がナルシシズム傾向の回答をしやすくて、特性値が高いと男女同程度のナルシシズム傾向の回答をしやすい、と言えそうです。

６．推論データ（idata）の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle
file = r'idata2_ch19.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata2, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata2_ch19.pkl'
with open(file, 'rb') as f:
    idata2_load = pickle.load(f)

以上で第19章は終了です。
そして、たのしいベイズモデリングは終了です。

おわりに

最終章

テキスト「たのしいベイズモデリング」は全１９章構成。
今回は最終章です。
たのしいベイズモデリング体験の機会をくださった、テキストの著者の先生、出版に関わった皆様、誠にありがとうございました。
そして、ブログを読んでくださった皆様、長期に渡ってお付き合いいただき、ありがとうございました。

最後に締めくくります。
姉妹書「たのしいベイズモデリング２」を利用させていただき、続編を実践したいと思います！

シリーズの記事

次の記事
テキストが「たのしいベイズモデリング２」に変わります

前の記事

目次

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ（お題）を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます！
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。

最後までお読みいただきまして、ありがとうございました。