この記事は、テキスト「たのしいベイズモデリング２」の第８章「統計モデリングで挑む『物語』」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

この章では、人気アニメーション作品「ヴァイオレット・エヴァーガーデン」の鑑賞者の反響をベイズモデリングで予測します。
作品構成に応じて３つの数理モデルを組み立てる序盤から、負の二項分布をモデリングする終盤まで、読者を魅了する見事なストーリーテリング。
ぜひテキストをお読みくださいね！

ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう！

テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。

サマリー

テキストの概要

執筆者　　　：　坂本次郎 先生
モデル難易度：　★★★★・　（やや難し）

自己評価

評点

$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい！ \\
\end{array}
$$

評価ポイント

• 久しぶりにテキストの結果とほぼ一致しました！
  嬉しいです！！！

工夫・喜び・反省

• 負の二項分布のパラメータに「平均」と「ばらつき」が使えることを知りました。正規分布みたいですね！
  今後は、離散値（カウントデータ）の確率分布を検討する際、観測値のばらつきを確認しつつ、ポアソン分布と負の二項分布を使い分けしたいです！

• ３つの数理モデルをベイズモデルに組み込む際に、数理モデルの使い分け・条件分岐をコード化する必要があります。
  条件分岐のコードについて、次の記事を参考にさせていただき、何とかPyMC5化できました。
  ありがとうございます！

モデルの概要

テキストの調査・実験の概要

■ 作品の紹介
この章は、ＴＶアニメーション作品「ヴァイオレット・エヴァーガーデン」を取り上げています。
Wikipediaでこの作品の概要を調べてみました。

• 2018年1月11日から2018年4月5日まで全13話が放映

• 原作は暁佳奈さんの小説「ヴァイオレット・エヴァーガーデン」

• 劇場版２編が映画化

Web検索の情報を読み進めるにつれて、多くの視聴者に愛されている作品なんだな、と実感しました。

■ データの概要
テキストは、秋葉原IT戦略研究所さん提供の「ShangriLa Amine API Server」から取得したデータを利用しています。
この記事でも秋葉原IT戦略研究所さん出典のデータをお借りします。
ありがとうございます！

データの略歴をテキストからお借りして記載します。
なおWikipediaの日付との１日ズレは、深夜24時以降の放送枠についてテキストが前日の日付を用いているからだと思われます。

• データは、初回放映日の2018年1月10日から最終話放映日以降6日間：4月10日までの期間の「作品公式Twitterアカウントのフォロワー増加数」です。

• 第12話放送日の3月28日の週と最終話放映日4月4日のデータが欠損しています。

まとめると、「欠損値を含む」フォロワー増加数の時系列データなのです。

■ この章が取り組む課題
先生は「（作品）構成を数量的にモデル化し、作品に対する実際の社会的反響を予測してみようというのが本章の具体的課題である」と仰っています。
作品構成には「序破急」からなる三部構成が仮定されます。
はじまりの「序」、展開の「破」、盛り上げてクライマックスを繰り広げる「急」。
テキストは、作品構成とフォロワー増加数を対応させる方向で数理モデルを構築しています。
作品のインパクトがTwitterのフォロワー増加数に影響する、という問題意識があられるようです。

■ 数理モデル
テキストの図8.2をお借りして、作品展開に応じた数理モデルのイメージを共有いたします。

左から、「序」の成分A、「破」の成分Ｂ、「急」の成分Ｃ、全成分を合算したDです。
グラフの横軸は作品の話数（物語の進行・時間経過）、縦軸は作品のインパクトを示す成分の強さです。
また、グラフタイトルには各成分の数理モデルを付記しています。

はじまりの「序」の成分Ａは、ガツンと強いインパクトからはじまって徐々に落ち着く曲線です。
「破」の成分Ｂは後半からじわじわと盛り上がりを見せる曲線です。
ラストの「急」は最終話で見せるクライマックスの盛り上がりに関わる曲線です。
３つの曲線を足したDを見ると、はじめの盛り上がり～中盤の落ち着き～ラストの大盛り上がりの様子がよく分かります。

各成分の数式表現です。テキストからお借りいたします。

序の主成分$${A_t}$$は、全13話の各話$${t,\ t=1, \cdots, 13}$$について、導入インパクト$${I}$$、インパクトの減衰傾向パラメータ$${\gamma}$$（$${0 \leq \gamma \leq 1}$$）を用いる指数関数$${\gamma^{t-1}}$$で表されます。

$${\gamma}$$は０～１の正の小数なので、話数が進むにつれて$${t-1}$$の値が大きくなり、$${\gamma^{t-1}}$$の値は小さくなります。

◆◆◆

破の主成分$${B_t}$$は、全13話の各話$${t,\ t=1, \cdots, 13}$$について、後半の上昇トレンドの上昇程度$${\beta}$$と、上昇に転じる転調起点を調整する$${d}$$（$${0 < d < 13}$$）を用いる指数関数$${\exp(t-d)}$$で表されます。

$${\exp(t-d)}$$は自然対数の底$${e}$$の$${t-d}$$乗のことです。
話数$${t}$$が$${d}$$より小さい、つまり上昇に転じる前は、$${t-d}$$は負の値になるため$${\exp(t-d)}$$は小さな値です。
一方で上昇に転じる話数$${d}$$を超えると、$${t-d}$$は正の値になるため$${\exp(t-d)}$$は大きな値＝上昇を示すことになります。

◆◆◆

急の主成分$${C_t}$$は、クライマックスがもつインパクトパラメータ$${R}$$（$${R > 0}$$）をクライマックスに切り替わるタイミング$${c}$$より後にのみ与える条件式で表されます。

クライマックスに切り替わるタイミング$${c}$$が12話だと仮定すると、第12話までは$${C_t}$$は０、つまりクライマックスインパクトは無い状態です。
第13話になるとクライマックスインパクト$${R}$$がガツンとやってきます！

これらの数理モデルが「ヴァイオレット・エヴァーガーデンのドラマ展開とファンの反響の関係性を分析」するベイズモデルに取り込まれます！
ベイズモデル＋数理モデル、なんかすごいことが起きそうです。

モデリングの前に～負の二項分布

テキストはさらにインパクト大のモデリングに進みます。
それは、目的変数である「フォロワー増加数$${Y_t}$$」が従う確率分布に「負の二項分布」を仮定することです！

■ 負の二項分布
負の二項分布は離散型確率分布です。
定義には次の２つがあるそうです。

1. 成功確率$${p}$$の独立した試行を繰り返すとき、$${r}$$回成功するまでの試行回数$${y}$$が従う分布

2. 成功確率$${p}$$の独立した試行を繰り返すとき、$${r}$$回成功するまでの失敗回数$${y}$$が従う分布

定義 2. の負の二項分布の確率質量関数のイメージ図を掲載します。
scipy.stats の nbinom を利用しました。

■ 負の二項分布の別の側面
ところが、テキストは負の二項分布の別の側面を教えてくれます。
それは「負の二項分布は平均$${\boldsymbol{\mu}}$$とばらつき（dispersion）$${\boldsymbol{\varphi}}$$の２つのパラメータを持つ確率分布」（定義 3）なのです。

定義 2. （$${y}$$は失敗回数）をベースにして、平均$${\mu}$$とばらつき$${\varphi}$$を用いて、成功確率$${p}$$と成功回数$${r}$$を計算すると、次式になるそうです。

この式は次のWebサイトの11ページの情報を引用いたしました。
ありがとうございます！

定義 3. （平均$${\mu}$$、ばらつき$${\varphi}$$）で負の二項分布の確率質量関数を描画してみます。

ばらつき$${\varphi}$$の値が大きくなるにつれて、峰が形成されて、峰の尖りが大きくなります。
峰の尖りが大きくなることは、ばらつきが小さくなるということです。
つまり、また$${\varphi}$$の値が大きくなると、ばらつきは小さくなります。

■ 負の二項分布とポアソン分布
上の図の曲線はポアソン分布の確率質量関数に似ています。
テキストは、ポアソン分布で表現しきれないときに負の二項分布を用いてモデリングすることを、そっと教えてくれました。

ばらつきパラメータ$${\varphi}$$が活躍するのですね！
$${\varphi=\infty}$$のとき、ポアソン分布と一致するそうです。
ぜひ、テキストで負の二項分布とポアソン分布の関係の式展開をご確認ください！

ポアソン分布との対比で負の二項分布の確率質量関数を描画してみましょう。

$${\varphi}$$の値が大きくなると負の二項分布はポアソン分布に近づきます。
$${\varphi=\infty}$$のとき、負の二項分布とポアソン分布が一致します。

■ 個人的な感動✨
パラメータに平均とばらつきを持つということは・・・
負の二項分布は離散変数・カウントデータの正規分布みたいな使い方ができそうです。
今後、カウントデータのベイズモデリングをするときには、ポアソン分布に加えて負の二項分布も活用していきたいです！

前振りが長くなってしまいました・・・

テキストのモデリング

■ モデリングと負の二項分布と数理モデル
テキストでは「フォロワー増加数$${Y_i}$$は平均$${\mu}$$、ばらつき$${\varphi}$$の負の二項分布に従う」としています。
そして平均$${\mu}$$には上述の３つの成分の和$${A_t+B_t+C_t}$$が用いられるのです。
負の二項分布と数理モデルのランデブー✨

■ 目的変数と関心のあるパラメータ
目的変数はフォロワーの増加数$${Y_{it}}$$です。
添字$${t}$$は全13話の放送回（$${t=1, \cdots, 13}$$）です。
添字$${i}$$は各放送回$${t}$$ごとの放送日からの週内経過日数（$${i=1, \cdots, 7}$$）です。
関心のあるパラメータは特段定めていないようです。
MCMCで計算・サンプリングする目的変数$${Y}$$の予測値に注目しています。

■ モデル数式
ひとまずテキスト掲載の数式を書きます。

■ パラメータの補足
$${w}$$（$${1 < w}$$）は放送日の推定フォロワー増加数$${\mu_t}$$に乗じる、持ち越し効果を示す係数「翌日持ち越し効果」です。
放送時間が平日深夜だったことから、録画して翌日に鑑賞する視聴者の存在を考慮するものです。
$${k}$$（$${0 \leq k \leq 1}$$）はフォロワー増加数の週内減少トレンドの減少係数です。
放送日翌日以降、次の放送日までの１週間の間にフォロワー増加数が減少トレンドがあることを考慮するものです。

■ パラメータの事前分布の補足
パラメータの事前分布については、一様分布を仮定します。
一様分布の範囲はテキストには明記されていません。
初期インパクト$${I}$$は初回放送日のフォロワー数$${y_{t=1}}$$とします。
成分$${C_t}$$のパラメータ$${R}$$は十分に大きな上限値（$${0 < R < 10000}$$）とし、最終話に加算することを想定されています。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。

PyMC実装

Let's enjoy PyMC & Python !

準備・データ確認

１．インポート

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

２．モデリングの説明に用いたプロット
「モデルの概要」章で用いた図を描画するコードを４本掲載します。

① 数理モデルによるストーリー展開の構成例
テキストの図8.2に相当します。

### 数理モデルによるストーリー展開の構成例 ※図8.2に相当

### 設定
## データ設定：t＝1～13
t = np.arange(1, 14)
## 描画設定
label = ['物語の進行 $t$', '成分の強さ', '合計']
title = ['A: $I \cdot r^{t-1}$', 'B: $\\beta \cdot e^{t-d}$',
         'C: $if\ t \leq c\ 0\ else\ R$', 'D (A+B+C)']
ylim = (-300, 7300)
bbox = (0, -0.15)
loc = 'upper left'

### 描画
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(12, 5))

## Aの描画
# パラメータ設定
I = 5000
rs = np.array([0.7, 0.8, 0.9])
At = np.zeros((len(rs), len(t)))
# パラメータrごとに折れ線グラフを描画
for i, r in enumerate(rs):
    # 数理モデルAt
    At[i] = I * r**(t-1)
    # 折れ線グラフの描画
    ax1.plot(t, At[i], '.-', label=f'r={r}, I={I}')
    # 修飾
    ax1.set(xlabel=label[0], ylabel=label[1], title=title[0], ylim=ylim)
    ax1.legend(bbox_to_anchor=bbox, loc=loc)
    ax1.grid(lw=0.3)

## Bの描画
# パラメータの設定
betas = np.array([1, 2, 3])
d = 6
Bt = np.zeros((len(betas), len(t)))
# パラメータβごとに折れ線グラフを描画
for i, beta in enumerate(betas):
    # 数理モデルBt
    Bt[i] = beta * np.exp(t-d)
    # 折れ線グラフの描画
    ax2.plot(t, Bt[i], '.-', label=f'$\\beta$={beta}, d={d}')
    # 修飾
    ax2.set(xlabel=label[0], ylabel=label[1], title=title[1], ylim=ylim)
    ax2.legend(bbox_to_anchor=bbox, loc=loc)
    ax2.grid(lw=0.3)

## Cの描画
# パラメータの設定
Rs = np.array([1000, 1500, 2000])
c = 12
Ct = np.zeros((len(Rs), len(t)))
# パラメータRごとに折れ線グラフを描画
for i, R in enumerate(Rs):
    # 数理モデルCt
    Ct[i] = [R if time > c else 0 for time in t]
    # 折れ線グラフの描画
    ax3.plot(t, Ct[i], '.-', label=f'$R$={R}, c={c}')
    # 修飾
    ax3.set(xlabel=label[0], ylabel=label[1], title=title[2], ylim=ylim)
    ax3.legend(bbox_to_anchor=bbox, loc=loc)
    ax3.grid(lw=0.3)

## D=A+B+Cの描画
# ３つのパラメータケースごとに折れ線グラフを描画
for i in range(3):
    # At+Bt+Ctを計算して折れ線グラフを描画
    ax4.plot(t, At[i] + Bt[i] + Ct[i], '.-',
             label=f'$r$={rs[i]}, $\\beta$={betas[i]}, $d$={d}, $R$={Rs[i]}')
    # 修飾
    ax4.set(xlabel=label[0], ylabel=label[2], title=title[3], ylim=ylim)
    ax4.legend(bbox_to_anchor=bbox, loc=loc)
    ax4.grid(lw=0.3)
plt.tight_layout();

【実行結果】

② 負の二項分布の確率質量関数 定義2

### 負の二項分布の確率質量関数 定義2
yvals = range(0, 21)
rvals = [3, 4, 5, 10]
for r in rvals:
    plt.plot(yvals, stats.nbinom.pmf(k=yvals, n=r, p=0.5), '-o', ms=5,
             label=f'$r={r}$')
plt.xlabel('失敗回数 $y$')
plt.ylabel('確率')
plt.title('負の二項分布 $nbinom(r, p)$：$p=0.5$')
plt.grid(lw=0.5)
plt.legend();

【実行結果】

③ 負の二項分布の確率質量関数 定義3 NegativeBinomial(μ,φ)

### 負の二項分布の確率質量関数 定義3 NegativeBinomial(μ,φ)
# 参考サイト https://www.slideshare.net/simizu706/ss-50994149

# 負の二項分布のパラメータの設定
mu = 7                          # μ
phis = np.array([1, 3, 10])     # φ
# パラメータpとrを計算して負の二項分布の確率質量関数を描画
for phi in phis:
    r = phi                     # 成功回数r
    p = phi / (mu + phi)        # 成功確率p
    plt.plot(yvals, stats.nbinom.pmf(k=yvals, n=r, p=p), '-o', ms=5,
             label=fr'$\phi={phi}$')
# 修飾
plt.xlabel('失敗回数 $y$')
plt.ylabel('確率')
plt.title(r'負の二項分布 $nbinom(\mu, \phi)$：$\mu=7$')
plt.grid(lw=0.5)
plt.legend();

【実行結果】

④ 負の二項分布の確率質量関数 定義3 NegativeBinomial(μ,φ)とポアソン分布

### 負の二項分布の確率質量関数 定義3 NegativeBinomial(μ,φ)とポアソン分布
# https://www.slideshare.net/simizu706/ss-50994149

# 負の二項分布のパラメータの設定
mu = 7                          # μ
phis = np.array([1, 3, 10, 100])     # φ
# パラメータpとrを計算して負の二項分布の確率質量関数を描画
for phi in phis:
    p = phi / (mu + phi)        # 成功確率p
    r = phi                     # 成功回数r
    plt.plot(yvals, stats.nbinom.pmf(k=yvals, n=r, p=p), '-o', ms=5,
             label=fr'負の二項分布 $\phi={phi}$')
# ポアソン分布の確率質量関数を描画
plt.plot(yvals, stats.poisson.pmf(k=yvals, mu=mu), '-o', ms=5,
            label=fr'ポアソン分布 $\mu={mu}$', color='black')
# 修飾
plt.xlabel('失敗回数 $y$')
plt.ylabel('確率')
plt.title(r'負の二項分布 $nbinom(\mu, \phi)$ : $\mu=7$と' + '\n'
          r'ポアソン分布 $poisson(\mu$)')
plt.grid(lw=0.5)
plt.legend();

【実行結果】

３．データの読み込み
csvファイルをpandasのデータフレームに読み込みます。

### データの読み込み
data_orgn = pd.read_csv('d.csv', encoding='cp932', parse_dates=['Date'])
display(data_orgn)

【実行結果】
92行のデータです。
Follwer列にはフォロワー数が設定されています。
次の前処理でフォロワー増加数を求めます。

４．データの前処理
pandas の diff() を用いて１日前（１行前）のフォロワー数を差し引き、フォロワー増加数を生成します。
また、モデルの都合で、データを全ての日付を含む「data_full」と放送日のみの「data_base」の２つに分けます。

### データの前処理

## data_fullの作成
# 読み込みデータのコピーを取得
data_full = data_orgn.copy()
# フォロワー増加数列の作成（1行前のフォロワー数を差し引く）、１行目を削除
data_full['Delta'] = data_full['Follower'].diff(1)
data_full = data_full.iloc[1:, :]
# 放送回（エピソード番号）列の作成：R・fullデータのEpisodeIndex
data_full['EpisodeNo'] = np.repeat(range(1, 14), 7)[:len(data_full)]
# 週番号列の作成：R・fullデータのInnerIndex
data_full['InnerNo'] = np.tile(range(1, 8), 13)[:len(data_full)][:len(data_full)]

## 放送日行のみを取り出したdata_baseの作成
data_base = data_full.query('OnAir == "放送日"').reset_index()

## 前処理後のデータ表示
display(data_full)
display(data_base)

【実行結果】
data_fullです。
Date列が日付、OnAirDate列が放送日、Delta列がフォロワー増加数、EpisodeNo列が放送回、InnerNoが週内の1～7の連番です。

data_baseです。放送日だけで絞っているのでデータ件数は13です。

５．フォロワー増加数の時系列プロットの描画
テキストの図8.3に相当します。

### Twitter公式アカウントのフォロワー増加数推移の描画 ※図8.3に相当

## データの準備
# 放送日の翌日日付の算出
nextdate = data_full.query('OnAir =="放送日"')['Date'] + pd.Timedelta(days=1)

## 描画
# 描画領域の指定
plt.figure(figsize=(12, 4))
# フォロワー増加数の描画
plt.plot(data_full['Date'], data_full['Delta'], '.-', color='tab:blue',
         label='フォロワー増加数')
# 放送日のフォロワー増加数の四角点の描画
plt.scatter(data=data_full.query('OnAir =="放送日"'), x='Date', y='Delta',
            marker='s', color='tab:blue', label=None)
# 放送日付の垂直線の描画
for date in data_full.query('OnAir =="放送日"')['Date']:
    plt.axvline(date, color='gray', lw=0.5)
# 放送日の翌日日付の垂直線の描画
for date in nextdate:
    plt.axvline(date, color='black', lw=0.8, ls='--')
# 放送日・放送日翌日の凡例用のダミー描画
plt.plot([], [], color='gray', lw=0.5, ls='--', label='放送日')
plt.plot([], [], color='gray', lw=0.8, ls='--', label='放送日の翌日')
# x軸目盛ラベルに放送日の翌日日付を表示
plt.xticks(nextdate, rotation=30)
# 修飾
plt.title(f'Twitter公式アカウントのフォロワー増加数推移')
plt.xlabel('日付')
plt.ylabel('フォロワー増加数')
plt.legend(loc='upper left');

【実行結果】
数理モデルの形状に似ている感じがします。
3月29日あたりは欠損値のためデータがありません。

モデル構築

モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。

$$
\begin{align*}
\gamma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
d &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=13) \\
\beta &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
R &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=10000) \\
w &\sim \text{Uniform}\ (\text{lower}=1,\ \text{upper}=10) \\
k &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
k_{final} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
\varphi &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=10000) \\
 \\
A_t &= Y_t \times \gamma^{t-1}, \quad \text{dims}=episodeNo \\
B_t &= \beta \times \exp (t-d), \quad \text{dims}=episodeNo \\
C_t &= [0,0,0,0,0,0,0,0,0,0,0,0,R]
 \\
\mu_t &= A_t + B_t + C_t, \quad \text{dims}=episodeNo \\
\mu_i &= \text{calc\_mui}, \quad \text{dims}=y_idata \\
 \\
Y_t likelihood &\sim \text{NegativeBinomial}\ (\text{mu}=\mu_t,\ \text{alpha}=\varphi,\ \text{dims}=episodeNo) \\
Y_i likelihood &\sim \text{NegativeBinomial}\ (\text{mu}=\mu_i,\ \text{alpha}=\varphi,\ \text{dims}=y_idata) \\
 \\
Y_tpred &\sim \text{NegativeBinomial}\ (\text{mu}=\mu_t,\ \text{alpha}=\varphi,\ \text{dims}=episodeNo) \\
Y_ipred &\sim \text{NegativeBinomial}\ (\text{mu}=\mu_i,\ \text{alpha}=\varphi,\ \text{dims}=y_idata) \\
\end{align*}
$$

１．モデルの定義
初期値とPyMC内で利用する関数を定義します。
calc_muI() は 条件に沿って muI の値を算出する関数です。

### モデル定義の準備

## 初期値設定
# 放送回（エピソード番号）のリスト化
episode_no = np.arange(1, 14)
# クライマックスタイミングc
c = 12

## muI計算関数 stanコードのmu_i[j]の計算ロジック
# 参考にした情報: https://qiita.com/Gyutan/items/691331556641ddbf88f3
def calc_muI(muT, epiNo, innerNo, c, w, k, kFinal):
    case1 = muT                                     # case1: 週の1日め
    case2 = muT * w * k**(innerNo - 2)              # case2: 0<放送回<=c
    case3 = muT * w * kFinal**(innerNo - 2)         # case3: 放送回>c
    return pt.switch(pt.eq(innerNo, 1),   case1,  
                     pt.switch(epiNo > c, case3,
                                          case2))

数式表現を実直にモデル記述します。
式中の「pt」は pytensor.tensor であり、テンソル計算処理に使用しています。

### モデルの定義
with pm.Model() as model:
    
    ### データ関連定義
    # coordの定義
    model.add_coord('yiData', values=data_full.index, mutable=True)
    model.add_coord('ytData', values=data_base.index, mutable=True)
    model.add_coord('epiNo', values=episode_no, mutable=True)
    # dataの定義
    yi = data_full['Delta'].values  # 欠損値を含むためConstantDataにできない
    yt = data_base['Delta'].values  # 欠損値を含むためConstantDataにできない
    epiNo = pm.ConstantData('epiNo', value=episode_no, dims='episodeNo')
    innerNoData = pm.ConstantData('innerNoData',
                                  value=data_full['InnerNo'].values,
                                  dims='yiData')
    epiNoData = pm.ConstantData('epiNoData',
                                  value=data_full['EpisodeNo'].values,
                                  dims='yiData')
    epiNoIdx = pm.ConstantData('epiNoIdx',
                               value=data_full['EpisodeNo'].values - 1,
                                dims='yiData')

    ### 事前分布
    gamma = pm.Uniform('gamma', lower=0, upper=1)    
    d = pm.Uniform('d', lower=0, upper=13)
    beta = pm.Uniform('beta', lower=0, upper=100)
    R = pm.Uniform('R', lower=0, upper=10000)
    w = pm.Uniform('w', lower=1, upper=10)
    k = pm.Uniform('k', lower=0, upper=1)
    kFinal = pm.Uniform('kFinal', lower=0, upper=1)
    phi = pm.Uniform('phi', lower=0, upper=10000)

    ### 数理モデルの計算
    ## 成分A = I * γ^(t-1)
    At = pm.Deterministic('At', yt[0] * pt.pow(gamma, (epiNo - 1)),
                          dims='episodeNo')
    ## 成分B = β * e^(t-d)
    Bt = pm.Deterministic('Bt', beta * pt.exp(epiNo - d),  dims='episodeNo')
    ## 成分C = 0 (if t<=c), R (if t>c)
    # 前半要素：c番目の要素まで0
    czeros = pt.tile([0], c)
    # 後半要素：c番目+1以後の要素はR
    cRs = pt.tile([R], episode_no.max()-c)
    # 成分C
    Ct = pm.Deterministic('Ct', pt.concatenate([czeros, cRs]), dims='episodeNo')
    
    ### muの計算
    # 放送回（エピソード番号）単位 
    muT = pm.Deterministic('muT', At + Bt + Ct, dims='episodeNo')
    # 全データレコード単位
    muI = pm.Deterministic('muI',
            calc_muI(muT[epiNoIdx], epiNoData, innerNoData, c, w, k, kFinal),
            dims='yiData')

    ### 尤度
    ytLikelihood = pm.NegativeBinomial('ytLikelihood', mu=muT, alpha=phi,
                                       observed=yt, dims='episodeNo')
    yiLikelihood = pm.NegativeBinomial('yiLikelihood', mu=muI, alpha=phi,
                                       observed=yi, dims='yiData')
    
    ### 計算値
    ytPred = pm.NegativeBinomial('ytPred', mu=muT, alpha=phi, dims='episodeNo')
    yiPred = pm.NegativeBinomial('yiPred', mu=muI, alpha=phi, dims='yiData')

【モデル注釈】

• coordの定義
  座標に名前を付けたり、その座標が取りうる値を設定できます。
  今回は次の３つを設定しました。

  • data_fullデータの行の座標：名前「yiData」、値「行インデックス」

  • data_baseデータの行の座標：名前「ytData」、値「行インデックス」

  • 放送回の座標：名前「epiNo」、値「1～13」

• dataの定義
  次の３つを設定しました。

  • 放送回：epiNo

  • 週内No：innerNoData

  • 放送回No：epiNoData

  • 放送回のインデックス：epiNoIdx

• パラメータの事前分布

  • モデルの数式表現のとおりです。

• 尤度

  • ２つの観測データごとに負の二項分布を設定しました。
    PyMC の 負の二項分布 NegativeBinomial のパラメータには、次の２つのいずれかの組み合わせを設定します。

    • 平均$${\mu}$$と形状$${\alpha}$$（$${\varphi}$$を設定）

    • 成功確率$${p}$$と成功回数$${n}$$

• 計算値 Y_pred

  • $${Y_t}$$と$${Y_i}$$の予測分布を尤度と同じ内容で設定しました。

２．モデルの外観の確認

# モデルの表示
model.basic_RVs

【実行結果】

# モデルの可視化
pm.model_to_graphviz(model)

【実行結果】
パラメータ数が多いこと、観測値に欠損値が含まれることなどの要因で、かなり複雑なモデルになっています。

３．事後分布からのサンプリング
観測値に欠損値を含む場合、numpyro が使えない（正確には使い方が分からない）ので、PyMCの標準サンプラーを利用します。
処理時間はおよそ9分でした。

### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを未使用　9分
# 観測データが欠損値を含み、計算値に離散型分布を用いるため、標準サンプラーを利用
# テキスト：iter=?, warmup=?, chains=?, adapt_delta=0.98
with model:
    idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.98,
                     random_seed=1234)

【実行結果】

４．サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。

### r_hat>1.1の確認
# 設定
idata_in = idata         # idata名
threshold = 1.1          # しきい値

# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()

【実行結果】
$${\hat{R} > 1.1}$$のパラメータは０件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。

### 推論データの要約統計情報の表示
pm.summary(idata, hdi_prob=0.95, round_to=3)

【実行結果】
369パラメータの推論を行ったようです。

トレースプロットで事後分布サンプリングデータの様子を確認します。

### トレースプロットの表示
pm.plot_trace(idata, compact=True)
plt.tight_layout();

【実行結果】
左のグラフから、４本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

分析

テキストにならって分析します。

MCMCでサンプリングしたフォロワー増加数$${Y_i, Y_t}$$の事後予測データをプロットします。
テキストの図8.4に相当します

### Twitter公式アカウントのフォロワー増加数推移と事後予測分布の描画 ※図8.4に相当

## 設定
int_type = 'CI'  # CI:信用区間, HDI:HDI区間

## データの準備
# 放送日の翌日日付の算出
nextdate = data_full.query('OnAir =="放送日"')['Date'] + pd.Timedelta(days=1)
# 95%区間、50%区間の算出
yi_pred = idata.posterior.yiPred.stack(sample=('chain', 'draw')).data
if int_type == 'CI':
    interval95 = np.quantile(yi_pred, q=[0.025, 0.975], axis=1).T
    interval50 = np.quantile(yi_pred, q=[0.250, 0.750], axis=1).T
else:
    interval95 = az.hdi(yi_pred.T, hdi_prob=0.95)
    interval50 = az.hdi(yi_pred.T, hdi_prob=0.50)

## 描画
# 描画領域の指定
plt.figure(figsize=(12, 4))
# フォロワー増加数の描画
plt.plot(data_full['Date'], data_full['Delta'], '.-', color='tab:blue',
         label='フォロワー増加数')
# 事後分布の95%HDIの描画
plt.fill_between(data_full['Date'], interval95[:, 0], interval95[:, 1],
                 color='tomato', alpha=0.2, label='95%区間')
# 事後分布の50%HDIの描画
plt.fill_between(data_full['Date'], interval50[:, 0], interval50[:, 1],
                 color='tomato', alpha=0.5, label='50%区間')
# 放送日のフォロワー増加数の四角点の描画
plt.scatter(data=data_full.query('OnAir =="放送日"'), x='Date', y='Delta',
            marker='s', color='tab:blue', label=None)
# 放送日付の垂直線の描画
for date in data_full.query('OnAir =="放送日"')['Date']:
    plt.axvline(date, color='gray', lw=0.5)
# 放送日の翌日日付の垂直線の描画
for date in nextdate:
    plt.axvline(date, color='black', lw=0.8, ls='--')
# 放送日・放送日翌日の凡例用のダミー描画
plt.plot([], [], color='gray', lw=0.5, ls='--', label='放送日')
plt.plot([], [], color='gray', lw=0.8, ls='--', label='放送日の翌日')
# x軸目盛ラベルに放送日の翌日日付を表示
plt.xticks(nextdate, rotation=30)
# 修飾
plt.title(f'Twitter公式アカウントのフォロワー増加数推移と事後予測分布'
          f' ({int_type}区間)')
plt.xlabel('日付')
plt.ylabel('フォロワー増加数と事後予測分布')
plt.legend(loc='upper left');

【実行結果】
テキストとほぼ一致していると思います！
数理モデル＆負の二項分布モデルは、作品のインパクトに沿ってフォロワー増加数をうまく推論できているようです。

テキストの89～90ページで用いられる翌日持ち越し効果$${w}$$と負の二項分布のばらつきパラメータ$${\varphi}$$の事後分布を確認します。

### パラメータw, φの事後統計量の表示 ※テキスト90ページの事後統計量に相当
params, stats = ['w', 'phi'], []
for param in params:
    sample = idata.posterior[param].data.flatten()
    ci95 = np.quantile(sample, q=[0.025, 0.975])
    stats.append([np.mean(sample), ci95[0], ci95[1]])
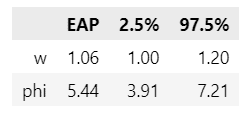
pd.DataFrame(stats, index=params, columns=['EAP', '2.5%', '97.5%']).round(2)

【実行結果】
翌日持ち越し効果$${w}$$は事後平均が$${1.06}$$、95%CIは$${[1.00,\ 1.20]}$$。
負の二項分布のばらつきパラメータ$${\varphi}$$は事後平均が$${5.44}$$、95%CIは$${[3.91,\ 7.21]}$$。
若干区間幅が広いですが、まあまあテキストに近い結果が得られています。

最後に放送日ごとのフォロワー増加数＆事後予測分布と成分$${A,B,C}$$の推定トレンドを確認します。
テキストの図8.5に相当します。

### ストーリー構成成分の推定結果の描画 ※図8.5に相当

## データ準備：yt_pred
# 95%区間、50%区間の算出
yt_pred = idata.posterior.ytPred.stack(sample=('chain', 'draw')).data
interval95 = np.quantile(yt_pred, q=[0.025, 0.975], axis=1).T
interval50 = np.quantile(yt_pred, q=[0.250, 0.750], axis=1).T

## データ準備：パラメータA, B, C
# 設定
params = ['At', 'Bt', 'Ct']   # 推論データから取り出すパラメータ
means, intervals = [], []     # 平均値、80%区間を格納するリスト
# パラメータごとに平均と80%区間を算出してリストに格納する
for i in range(len(params)):
    # 推論データからパラメータのサンプルデータを取り出し
    tmp = idata.posterior[params[i]].stack(dat=('chain', 'draw')).data
    # 平均値の算出
    means.append(tmp.mean(axis=1))
    # 80%CI区間の算出 np.quantileで10%点と90%点を取得
    intervals.append(np.quantile(tmp, q=[0.1, 0.9], axis=1))

## 描画設定：初期値
title = ['A', 'B', 'C']
ylim = (-300, 5000)
xticklabels = data_base['EpisodeNo'].values

## 描画設定：描画領域
# 描画領域の指定
fig = plt.figure(figsize=(7, 6))
# Grid領域の指定
grid = plt.GridSpec(3, 2)
# yt_predのGrid領域
ax1 = fig.add_subplot(grid[0:, 0])
# A, B, CのGrid領域
ax2 = fig.add_subplot(grid[0, 1])                          # A
ax3 = fig.add_subplot(grid[1, 1], sharex=ax2, sharey=ax2)  # B
ax4 = fig.add_subplot(grid[2, 1], sharex=ax2, sharey=ax2)  # C
ax = [ax2, ax3, ax4]                                       # [A, B, C]

## 描画処理：yt_pred
# フォロワー増加数の描画
ax1.plot(data_base['EpisodeNo'], data_base['Delta'], 'o',
         label='フォロワー増加数')
# 95%CI・50%CIの描画
ax1.fill_between(x=data_base['EpisodeNo'],
                 y1=interval95[:, 0], y2=interval95[:, 1],
                 color='tomato', alpha=0.2, label='95%CI')
ax1.fill_between(x=data_base['EpisodeNo'],
                 y1=interval50[:, 0], y2=interval50[:, 1],
                 color='tomato', alpha=0.5, label='50%CI')
# 修飾
ax1.set(xlabel='物語の進行（アニメ本編全13話）',
        ylabel='放送日のフォロワー増加数と事後予測分布',
        xticks=xticklabels, xticklabels=xticklabels)
ax1.legend(loc='upper left')
ax1.grid(lw=0.5);

## 描画処理：パラメータA, B, C
# パラメータごとに描画を繰り返し処理
for i in range(len(params)):
    # エラーバーグラフの描画
    ax[i].errorbar(x=xticklabels, y=means[i], yerr=abs(intervals[i] - means[i]),
                   fmt='.-')
    # 修飾
    ax[i].set(title=title[i], xticks=xticklabels, ylim=ylim,
              yticks=[i*1000 for i in range(5)])
    ax[i].grid(lw=0.3)
# A,B,C共通修飾
ax[1].set_ylabel('事後平均')
ax[2].set_xlabel('物語の進行（アニメ本編全13話）')
# 全体修飾
fig.suptitle('ストーリー構成成分の推定結果')
plt.tight_layout()
plt.show()

【実行結果】
テキスト75ページの数値とほぼ同じ結果になりました。
「物語の構成：序破急」「ヴァイオレット・エヴァーガーデンのドラマ展開」「ファンの反響」が数理モデルを通じて三位一体になっています！

左のフォロワー増加数の事後予測のＪ型はスタートとクライマックスの盛り上がりを表現できている感じです。
右の各成分を見ると、「序」の成分$${A}$$は第１話で2500程度のインパクトを演出した後、緩やかに減少しています。
「破」の成分$${B}$$は第８話あたりからインパクトが生み出されて最終話では2500程度にまで上昇しています。
「急」の成分$${C}$$は最終話に加算されるものであり、平均1500程度ですが、縦線（80%CIエラーバー）が長くなっていて、予測幅が広くなっています。

物語の構成「序破急」に基づく数理モデル、負の二項分布による表現力の凄さを感じまくっています。

そういえば負の二項分布の平均パラメータが気になりました。
$${\mu_i}$$の形状を確認しましょう。

### 平均パラメータmu_iの中央値とHDIを描画
# mu_Iの取得
mu_i_samples = idata.posterior.muI.stack(sample=('chain', 'draw')).data
# mu_Iの95%HDIと50%HDIの算出
mu_i_hdi95 = az.hdi(mu_i_samples.T, hdi_prob=0.95).T
mu_i_hdi50 = az.hdi(mu_i_samples.T, hdi_prob=0.50).T
# 描画領域の指定
plt.figure(figsize=(10, 4))
# 観測値の描画
plt.plot(data_full['Date'], data_full['Delta'], 'o', color='blue', alpha=0.5,
         label='観測値 $Y_i$')
# mu_iの中央値の描画
plt.plot(data_full['Date'], np.median(mu_i_samples, axis=1), '-o',
         color='red', alpha=0.5, label='$\mu_i$：中央値')
# mu_iの95%HDIの描画
plt.fill_between(data_full['Date'], mu_i_hdi50[0], mu_i_hdi95[1],
                 color='tomato', alpha=0.2, label='$\mu_i$：HDI95%')
# mu_iの50%HDIの描画
plt.fill_between(data_full['Date'], mu_i_hdi50[0], mu_i_hdi50[1],
                 color='tomato', alpha=0.5, label='$\mu_i$：HDI50%')
# 修飾
plt.title('観測値 $Y_i$,  平均パラメータ$\mu_i$ の中央値・95%HDI・50%HDI')
plt.xlabel('日付')
plt.ylabel('フォロワー増加数')
plt.grid(lw=0.5)
plt.legend(loc='upper left');

【実行結果】
平均パラメータも素敵な線を描いてくれました。
大まかにはインパクトの波を捕まえているようです。

最後に、推論データを再利用する（かもしれない）場合に備えてファイルに保存しましょう。
idataをpickleで保存します。

### idataの保存 pickle
file = r'idata_ch08.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata, f)

読み込みコードは次のとおりです。

### idataの読み込み pickle
file = r'idata_ch08.pkl'
with open(file, 'rb') as f:
    idata_load = pickle.load(f)

以上で第８章は終了です。

おわりに

アニメーション作品

普段は時々アニメーション作品を鑑賞します。
直近はスパイファミリー。
読心力がほしいな、なんて思いつつ、くすくす笑って見ています。

おわり

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。