ゲーム理論(岡田章)第３章

前回の記事の続きになる。

紹介する参考書はこちら。

展開形ゲームとは

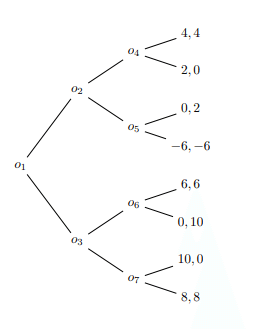
復習として、前回の戦略形ゲームは各プレイヤーが他のプレイヤーの行動を推定し、それぞれが同時に１回の戦略を表出するというゲームであった。しかし、例えば将棋などの手番が存在するゲームを考えてみると、各プレイヤーが１回の表出で終わる訳では無く、手番と言う概念(※図における各$${o_i}$$のこと)が存在し、各プレイに対し(有限回の)手番を通し終了するというモデルが考えられるだろう。このゲームを一般に展開ゲームと呼ぶ。実際には、展開形ゲームは標準化と呼ばれる操作(※つまり相手の全ての手番における戦略を推定し「こうきたらこう！」というのをゲームが始まる前にお互いが予め全て決めておけば、ある意味時間について並列化した、即ち全通り並べ立てたただ１つの戦略は戦略形ゲームの戦略である)を通して戦略形ゲームとして見れる故、戦略形ゲームの任意の定理が成立するのだが、展開ゲームは手番的(※時間軸的)本質(※形式的に見ると戦略ゲームの具体例にすぎないかもしれないが意味的にそれを超える)を有するのでその付近の性質をくみ取っていきたいというのがやりたい事になる。

展開形ゲームの数理モデル

展開形ゲームは形式的に$${\Gamma = (K,P,p,U,h)}$$として決定される。

ゲームの木K

$${K}$$はゲームの木である。他の分野における木と同じようにnodeとedgeを持つ。ゲームの終結地点のnodeを頂点と呼び、それ以外のnodeを手番と呼ぶ。ゲームのプレイとは初期値$${o_1}$$から頂点へのパスである。

プレイヤー分割P

ゲームにはプレイヤー$${P_i}$$が存在する。suffix 0はコインを振る等の偶然手番に用い、利得を受け取るプレイヤーはsuffix 1から始めるのが良い。即ち手番全体$${X}$$の部分集合として決定すればよく、$${P_0 = \{o_1\}, P_1 = \{o_2, o_3\}, P_2 = \{o_4, o_5, o_6, o_7\}}$$とするのが良いだろう。

偶然手番の確率分布族p

任意の偶然手番$${x}$$に対して確率分布$${p_x}$$の存在を仮定する。

情報分割U

最も重要な概念である。プレイヤー分割の再分割$${P_i = \cup_{u \in U_i}u}$$として定義される$${U = (U_i)}$$は、各プレイヤーが現在どの手番に到達しているのかを知っているか知らないかのモデルである。即ち、仮に図において$${U_2 = \{P_2\}}$$と定義した時、プレイヤー2は自身の手番が$${o_4, o_5, o_6, o_7 }$$のどれであるかを知らないとみなす。
この時例えば各手番において上のパスに進む選択を$${H}$$、下のパスに進む選択を$${L}$$とした時、プレイヤー2が$${H}$$を選んだとして得る事の出来る利得は上から4, 2, 6, 0のどれかであるが、それを特定することは出来ない。

利得関数h

各頂点$${w}$$に対して利得ベクトル$${h(w) = (h_i(w))}$$の存在を仮定する。図でいうと最上部$${w}$$の利得ベクトル$${h}$$は$${(4,4)}$$となる。

完全情報ゲーム

情報分割によって各プレイヤーの既知の範囲が明確になったが、将棋等の展開形ゲームにおいては相手が指した手が何かが分かるというルールが設けられている。この先は簡単の為、各プレイヤーが今どの手番$${x}$$にいるかが判別的な場合のみ述べる。これを完全情報ゲームと呼ぶ。情報分割の言葉に還元すると、任意の$${u}$$は単独の手番からなるという事である。(※つまりこの記事においては情報分割が成す深みに立ち入らないという事である)

ゲームの分解と合成

行動戦略(※混合戦略。各々は確率分布と見做しても良い。)の組$${b^\ast = (b^\ast_{i})}$$が均衡プレイというのは戦略形におけるそれと同様な形で定義される。即ち、任意のプレイヤー$${i}$$は戦略を$${b_i^\ast}$$から変更したとしても期待利得が上がる事は無いという事である。また部分ゲーム$${\Gamma^{'}}$$というのは、ゲームの木の部分木から作られるゲームで元のゲームから自然と導かれるものである(※例えば$${X^{'} = \{o_3, o_6, o_7\}}$$)。
この時、均衡プレイはそのパス上に存在する任意の部分ゲームの均衡プレイを導き、かつその部分ゲームにより縮約されたゲーム(※例えばかなり形式的に書くとすると$${X(\Gamma) = \{o_1, o_2, o_4, o_5, X(\Gamma^{'})\}}$$。これはいわば元ゲームに対して部分ゲームをブラックボックスにしたゲームであり、$${X^{'}}$$自体を頂点として見たゲーム)の均衡プレイに分解できる。これがゲームの分解定理である。合成とは逆にとある部分ゲームとその縮約ゲームの均衡プレイから自然に導かれるプレイは均衡プレイであるという主張になる。

backward induction

更に完全情報ゲームでは後ろ向き帰納法(backward induction)と呼ばれる純戦略である均衡プレイを求める定理(※アルゴリズム)が存在する。定理の証明は省略するが、まず頂点に最も近い各部分ゲーム$${X_1={o_4}, X_2={o_5}, X_3={o_6}, X_4={o_7}}$$(※この手番からなる部分ゲーム$${\Gamma_i}$$)の(プレイヤー2の)最適応答を求める。さらにこの部分ゲームを真に含む最小の部分ゲーム(※例えばそのひとつは形式的に言って$${\{o_2, X(\Gamma_1), X(\Gamma_2)\}}$$である)のプレイヤー1の最適応答を求める。そしてこの縮約ゲームと最初の部分ゲームを合成し、各プレイを構成する(※図の場合は２つ。各々それは部分ゲームのプレイである)。これを初期値$${o_1}$$まで繰り返すとひとつのプレイを構成することが出来るが、実はこれが均衡プレイとなっているのである。

まとめ

今回は展開形ゲームのモデリングと主要な定理(※そしてアルゴリズム)を紹介しました。例えばbackward induction用いるとプレイヤーの時間軸的な戦略の均衡点などを求めることが出来ます。典型的な例としては同財を供給するリーダー企業とフォロワー企業があった場合に、費用や供給量に対する価格等の定数が判明している時に、均衡プレイ上の各々の供給量、利益、財の市場価格等を具体的に求めることが出来ます(※シュタッケルベルク均衡)。
この理論を使った具体例はいつか機会があれば述べるとしますが、知ってもらいたいのは、土台には部分ゲームの分解・合成における数学的な証明が存在するということです。今回は理論のみに留めます。

スキ、フォロー、シェアお願いいたします！では！！