こんにちは、Junです。

前回は、三角比・三角関数について書きましたが、
今回は、指数と対数について書いていきます。

⒈ 指数

i. 指数の定義

$$
a^p
$$

で表される式の中の$${a}$$を底（てい）、$${p}$$を指数と言います。

ii. 指数法則

指数には様々な法則があります。

(1)$${a^m \times a^n=a^{m+n}}$$

(例) $${2^3\times2^2=2^{3+2}=2^5=32}$$

(2)$${\frac{a^m}{a^n}=a^{m-n}}$$

例) $${\frac{2^3}{2^2}=2^{3-2}=2^1=2}$$

(3)$${(a^m)^n=a^{mn}}$$

(例) $${(2^3)^2=2^6=64}$$

(4)$${a\ne0}$$の時、$${a^0=1}$$

(2)に$${n=m}$$を代入してみれば、約分して1になることがわかる。

(例) $${2^0=1}$$

(5)$${a^{-n}=\frac{1}{a^n}}$$

(2)に$${m=0}$$を代入してみれば、逆数になることがわかる。

(例) $${2^{-1}=\frac{1}{2}}$$

(6)$${a^{\frac{m}{n}}=\sqrt[n]{a^n}}$$

(例) $${2^{\frac{1}{2}}=\sqrt{2}}$$

練習問題

次の計算をせよ

(1)$${3^4\times\ 3^2}$$

(2)$${\frac{5^4}{5^2}}$$

(3)$${(4^2)^3}$$

(4)$${2^2\div 2^{-3}\times 2^{\frac{1}{2}}}$$

iii. ネイピア数e

ここで一旦金利の話になります。

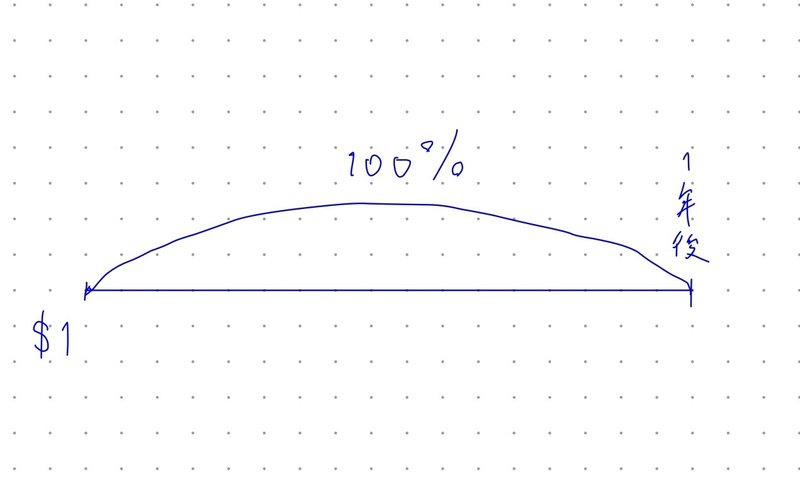
もし、1月に1ドルを預けて、1年後に100%の利息をもらえるとすると、1年後には、

$${(1+1)=2}$$で、2ドルになっています。

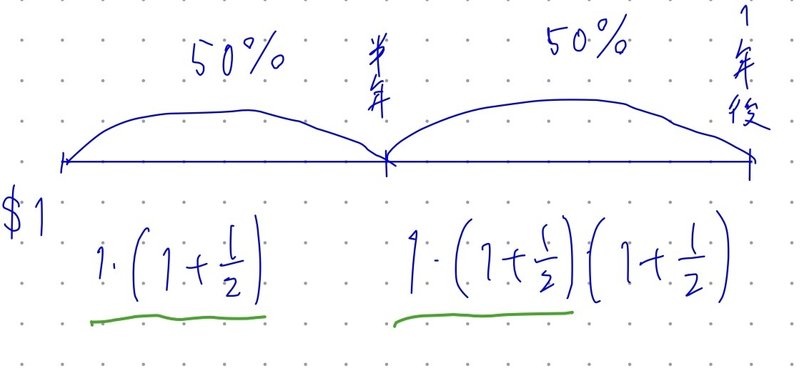
では、1月に1ドルを預けて、半年ごとに50%ずつ利息をもらえるとすると、上半期には、

$${(1+\frac{1}{2})=1.5}$$ドル、

1年後には、

$${(1+\frac{1}{2})(1+\frac{1}{2})=(1+\frac{1}{2})^2=2.25}$$ドルになっています。

では、1月に1ドルを預けて、四半期ごとに25%ずつ利息をもらえるとすると、

第一四半期には、

$${(1+\frac{1}{4})=1.25}$$ドル、

第二四半期には、

$${(1+\frac{1}{4})(1+\frac{1}{4})=(1+\frac{1}{4})^2=1.5625}$$ドル、

第三四半期には、

$${(1+\frac{1}{4})^2(1+\frac{1}{4})=(1+\frac{1}{4})^3=1.953125}$$ドル、

1年後には、

$${(1+\frac{1}{4})^3(1+\frac{1}{4})=(1+\frac{1}{4})^4=2.44140625}$$ドル、

になっています。

この法則から、1年間にn回に分けて利息をもらえるとすると、1年後には、

$${(1+\frac{1}{n})^n}$$ドル貰えることになります。

ここで、1年間に利息を無限回貰えるとすると、上のnを限りなく大きくしていき、

$$
\lim_{n \to \infty}(1+\frac{1}{n})^n
$$

とすると、

2.71828…

という、無理数になっていきました。

この値をeと置いて、定義することにしました。

このeのことを、ネイピア数または自然対数の底と言います。

$$
\lim_{n \to \infty}(1+\frac{1}{n})^n = e
$$

このeはとても使い勝手が良いので、数学や物理学などでよく用いられます。

⒉ 指数関数

i. 指数関数の定義

$${y=a^x}$$（ただし、$${a>0,  a\ne1}$$）のような関数を指数関数と言います。

$${a\le0}$$を定義しない理由

$${a=0}$$の場合、$${a^{-1}}$$などを定義できないことと、

例えば$${a=-1}$$の場合、$${(-1)^\frac{1}{2}=\sqrt{-1}=i}$$と、虚数になってしまい、目盛りを打てないため、定義していません。

$${a=1}$$を定義しない理由

$${a=1}$$とすると、$${y=1}$$となり、傾き0の一次関数となってしまうため、指数関数としては扱いません。

ii. 指数関数のグラフ

$${a>1}$$の場合

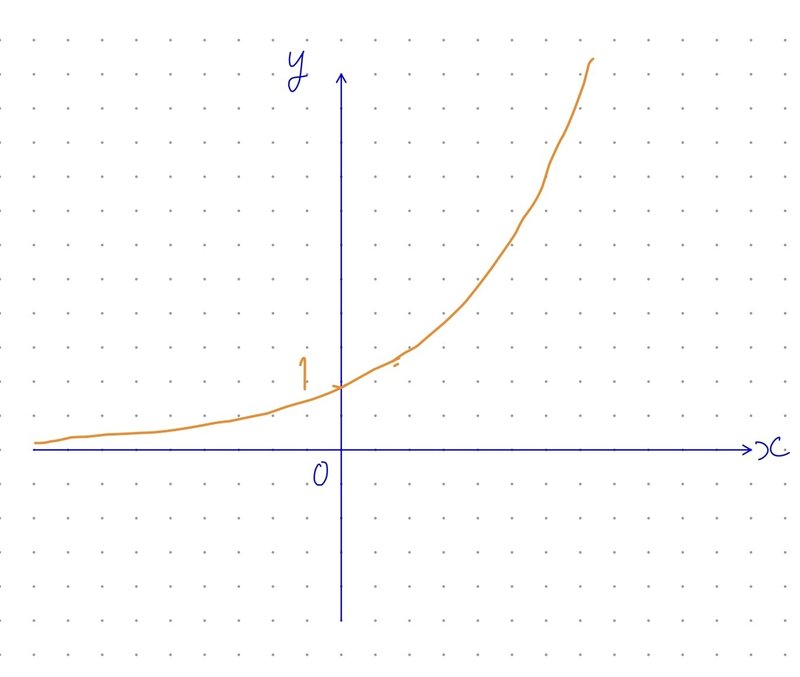
このように、右上がりの曲線になっています。

必ず、(0, 1)を通ります。

特に、$${y=e^x}$$のグラフは、

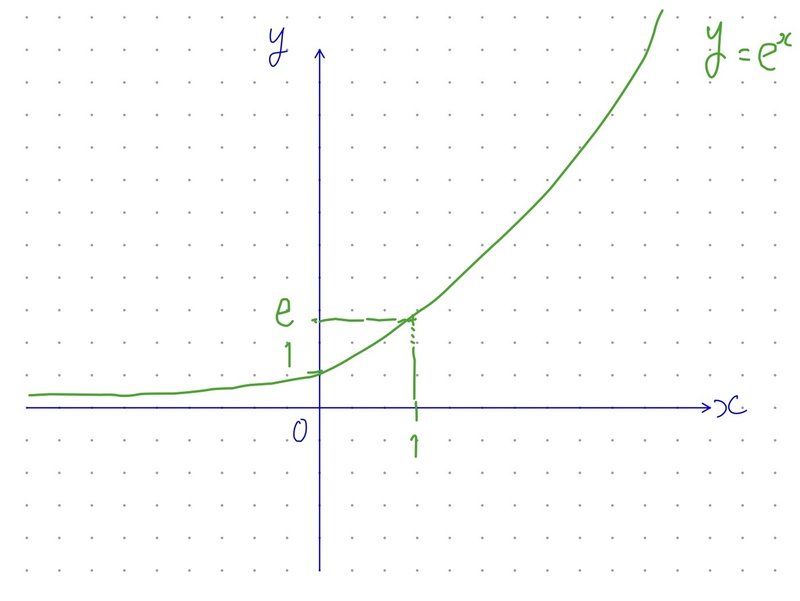
となります。

$${0< a < 1}$$の場合

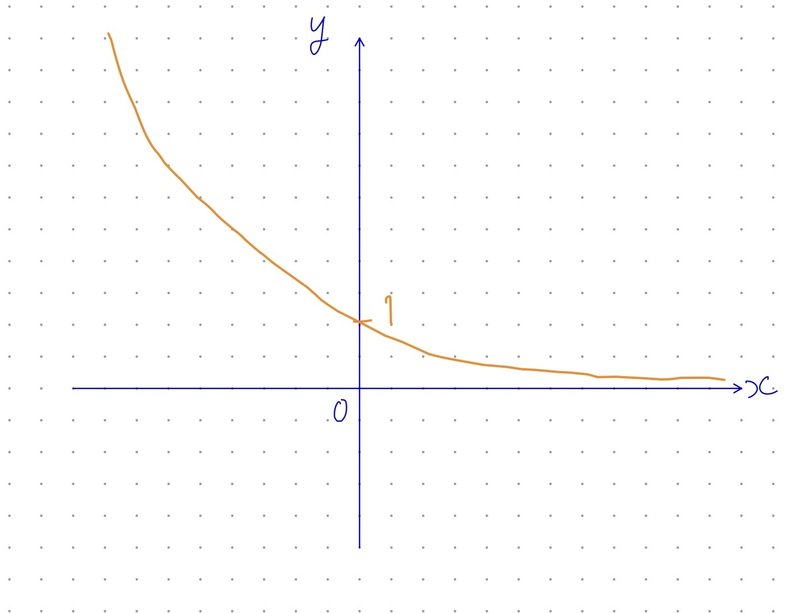
このように、右下がりの曲線になっています。

必ず、(0, 1)を通ります。

⒊ 対数

i. 対数の定義

$${2^x=4}$$であるとき、$${x=2}$$であるすぐにわかります。

$${2^x=\sqrt{2}}$$であるとき、指数法則から$${x=\frac{1}{2}}$$であるとわかります。

では、$${2^x=3}$$であるとき、$${x}$$の値はいくらでしょうか？

この$${x}$$を$${\log_{2}3}$$と表記し、これを対数と言います。

そして、

$$
\log_{a}b
$$

の$${a}$$を底（てい）といい、$${b}$$を真数と言います。

さらに、
底の条件は、指数関数と同様に$${a > 0,  a \ne 1}$$、
真数の条件は、$${b > 0}$$です。

$${\because  x=\log_{a}b}$$の時、$${b=a^x}$$で、常に$${a^x > 0}$$であるから。

また、

$${\log_{a}1=0,  \log_{a}a=1}$$も成り立ちます。

ii. 対数の公式

・$${\log_{a}xy = \log_{a}x+\log_{a}y}$$

$${\because }$$指数法則(1)で、
$${a^m = x,  a^n = y, a^{m+n}=z}$$とおくと、

$$
m=\log_{a}x,  n=\log_{a}y,  m+n=\log_{a}z
$$

$${z=xy}$$であるから、それぞれを代入して、

$$
\log_{a}x+\log_{a}y=\log_{a}xy
$$

・$${\log_{a}\frac{x}{y} = \log_{a}x-\log_{a}y}$$

$${\because }$$指数法則(2)で、
$${a^m = x,  a^n = y, a^{m-n}=z}$$とおくと、

$$
m=\log_{a}x,  n=\log_{a}y,  m-n=\log_{a}z
$$

$${z=\frac{x}{y}}$$であるから、それぞれを代入して、

$$
\log_{a}x-\log_{a}y=\log_{a}\frac{x}{y}
$$

・$${\log_{a}x^n = n\log_{a}x}$$

$${\because }$$指数法則(3)で、
$${a^m = x, a^{mn}=z}$$とおくと、

$$
m=\log_{a}x,  mn=\log_{a}z
$$

$${z=x^n}$$であるから、

$$
(\log_{a}x) \cdot n = \log_{a}x^n  \Leftrightarrow  \log_{a}x^n=n\log_{a}x
$$

・底の変換公式

$${c>0,  c\ne1}$$を用いて、

$$
\log_{a}b=\frac{\log_{c}b}{\log_{c}a}
$$

と変換できる。

$${\because}$$

$${x=\log_{a}b}$$とおくと、

$$
a^x=b
$$

両辺に底$${c}$$の対数をとると、

$$
\log_{c}a^x=\log_{c}b
$$

$$
x\log_{c}a=\log_{c}b,  x=\frac{\log_{c}b}{\log_{c}a}
$$

よって、

$$
\log_{a}b = \frac{\log_{c}b}{\log_{c}a}
$$

練習問題

次の式を簡単にせよ。

(1)

$$
\log_{2}9\cdot\log_{3}5\cdot\log_{5}\sqrt{2}
$$

(2)

$$
\log_{2}\frac{2}{3}+\log_{2}9
$$

iii. 常用対数

底が10である対数のことを、常用対数と言い、

$$
\log_{10}b
$$

または、底を省略して、

$$
\log b
$$

と書くこともあります。（このnoteでは底を省略しない書き方を採用します）

この常用対数を用いると、$${2^{50}}$$などの桁数を求めることができます。

$${\log_{10}2=0.3010}$$とすると、

$$
\log_{10}2^{50}=50\times\log_{10}2=50\times 0.3010 =15.05
$$

これより、

$$
15 < \log_{10}2^{50} <16  
$$

つまり、

$$
10^{15} < 2^{50} < 10^{16}
$$

となり、$${2^{50}}$$は16桁の整数であることがわかります。

練習問題

$${5^{20}}$$は何桁の整数かを求めなさい。
ただし、$${\log_{10}2=0.3010}$$とします。

iv. 自然対数

底がネイピア数eである対数のことを自然対数といい、

$${\log_{e}b,  \log b,  \ln b}$$などと書きます。
このnoteでは$${\log b}$$を採用します。

⒋ 対数関数

i.  対数関数

$${y=\log_{a}x}$$のように表される関数を対数関数と言います。

ii. 対数関数のグラフ

対数関数のグラフは以下のようになります。

$${a > 1}$$の場合、

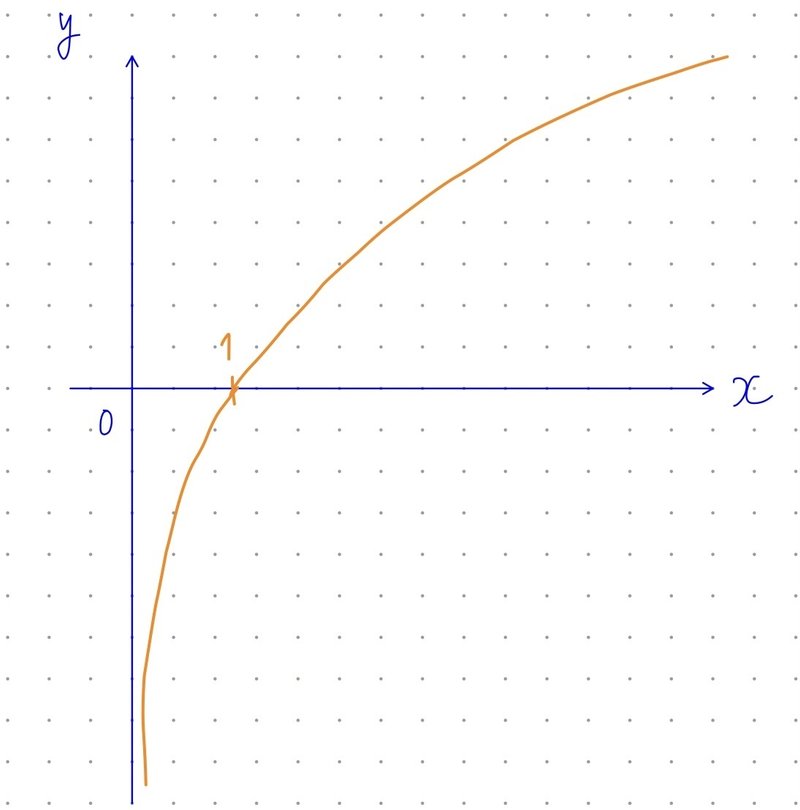
右上がりの曲線で、
必ず(1, 0)を通ります。

特に、$${y=\log x}$$のグラフは、

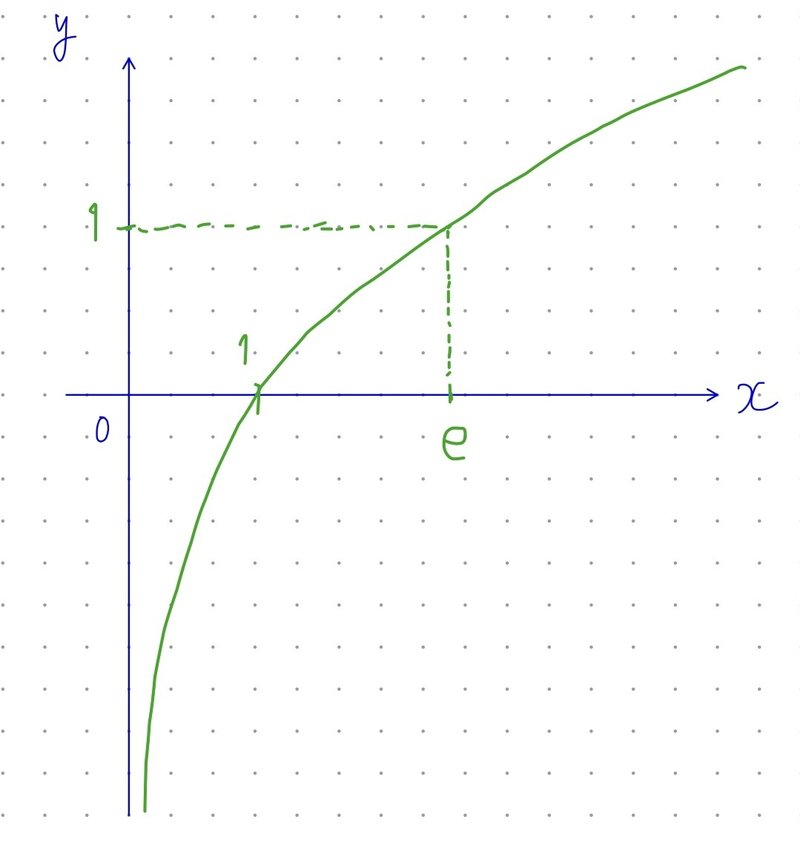
となります。

$${0 < a < 1}の場合、

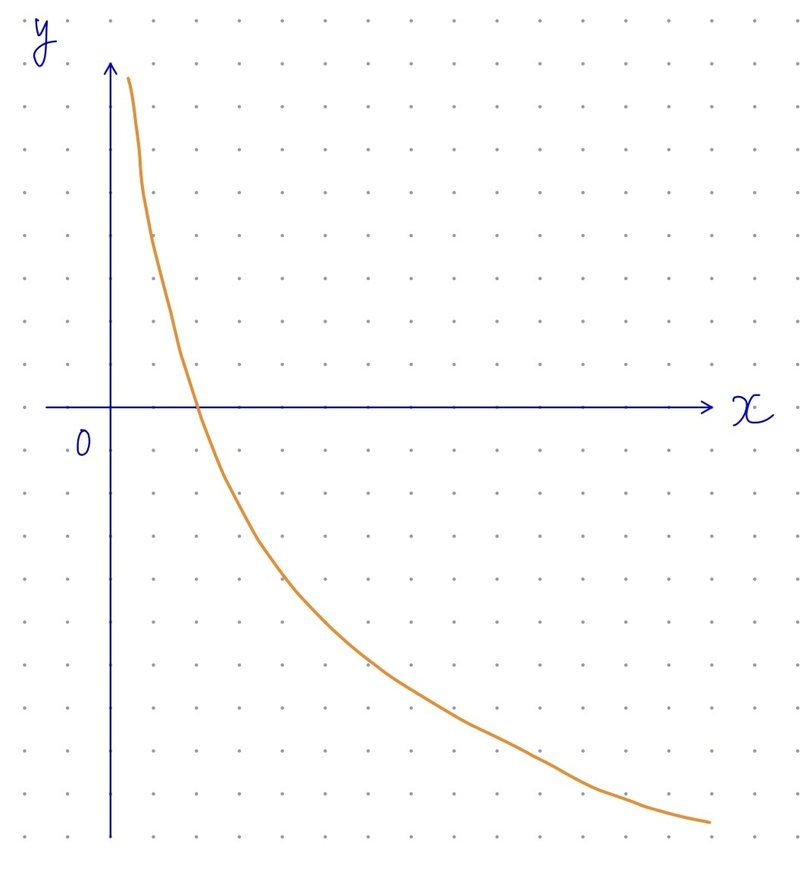
右下がりの曲線で、
必ず(1, 0)を通ります。

⒌ 指数関数・対数関数の微分

i. 指数関数の極限公式

$$
\lim_{x \to 0}\frac{e^x-1}{x} = 1
$$

【証】
$$
\lim_{t \to \infty}(1+\frac{1}{t})^t=e
$$

であるから、

$$
\lim_{t \to \infty} \log(1+\frac{1}{t})^t=1
$$

ここで、$${t=\frac{1}{u}}$$とおくと、$${t \to \infty}$$の時、$${u \to 0}$$

$$
\lim_{t \to \infty} \log(1+\frac{1}{t})^t=\lim_{u \to 0}\log(1+u)^{\frac{1}{u}}
$$

$$
=\lim_{u \to 0}\frac{1}{u} \log(1+u)=\lim_{u \to 0}\frac{\log(1+u)}{u}=1
$$

これより、逆数を取っても1に収束するので、

$$
\lim_{u \to 0}\frac{u}{\log (1+u)} = 1
$$

さらにここで、$${x=\log(1+u)}$$とおくと、$${1+u=e^x,  u=e^x-1}$$で、
$${u \to 0}$$の時、$${x \to 0}$$なので、

$$
\lim_{u \to 0}\frac{u}{\log (1+u)} = \lim_{x \to 0} \frac{e^x-1}{x}=1
$$

【証明終】

i. 指数関数の微分

(1)$${(e^x)'=e^x}$$

【証】

$$
(e^x)'=\lim_{\Delta x \to 0}\frac{e^{x+\Delta x}-e^x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{e^x(e^{\Delta x}-1)}{\Delta x} = e^x\lim_{\Delta x \to 0}\frac{e^{\Delta x}-1}{\Delta x} = e^x
$$

（$${\because}$$ $${\lim_{\Delta x \to 0}\frac{e^{\Delta x}-1}{\Delta x}=1}$$）

【証明終】

(2) $${(a^x)'=a^x\log a}$$

【証】

$$
(a^x)'=\lim_{\Delta x \to 0}\frac{a^{x+\Delta x}-a^x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{a^x(e^{\Delta x}-1)}{\Delta x} = a^x\lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x} 
$$

ここで、

$$
\lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x}=\lim_{\Delta x \to 0}\frac{e^{\log{a^{\Delta x}}}-1}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{e^{\Delta x\log{a}}-1}{\Delta x}=\lim_{\Delta x \to 0}\frac{e^{\Delta x\log{a}}-1}{\Delta x\log a}\cdot\log a=\log a
$$

（$${\because}$$ $${\lim_{\Delta x \to 0}\frac{e^{\Delta x\log{a}}-1}{\Delta x\log a}=1}$$）

$$
\therefore   (a^x)'=a^x\log a
$$

【証明終】

ii. 対数関数の微分

(1) $${(\log x)'=\frac{1}{x}}$$

【証】

$$
(\log x)'=\lim_{\Delta x \to 0}\frac{\log(x+\Delta x)-\log x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{1}{\Delta x}\{\log(x+\Delta x)-\log x\}=\lim_{\Delta x \to 0}\frac{1}{\Delta x}\log\frac{x+\Delta x}{x}
$$

$$
=\lim_{\Delta x \to 0}\log(1+\frac{\Delta x}{x})^{\frac{1}{\Delta x}}
$$

$$
=\lim_{\Delta x \to 0}\log\{(1+\frac{\Delta x}{x})^{\frac{x}{\Delta x}}\}^\frac{1}{x}
$$

$$
=\frac{1}{x}\lim_{\Delta x \to 0}\log\{(1+\frac{\Delta x}{x})^{\frac{x}{\Delta x}}\}=\frac{1}{x}
$$

$$
\therefore  (\log x)'=\frac{1}{x}
$$

【証明終】

(2) $${(\log_{a}x)'=\frac{1}{x\log a}}$$

【証】

$$
(\log_{a}x)' = (\frac{\log x}{\log a})'=\frac{1}{\log a}(\log x)'=\frac{1}{\log a}\frac{1}{x}
$$

$$
=\frac{1}{x\log a}
$$

$$
(\log_{a}x)'=\frac{1}{x\log a}
$$

【証明終】

⒍ 指数関数・1/xの積分

i. 指数関数の積分

(1)

$${(e^x)'=e^x}$$であるから、

$$
\int e^x dx = e^x+C
$$

(2)

$${(a^x)'=a^x\log a}$$であるから、

$$
\int a^x dx = \frac{a^x}{\log a}
$$

ii. 1/xの積分

$${(\log x)' = \frac{1}{x}}$$であるから、

$$
\int \frac{1}{x} dx = \log|x| +C
$$

多項式関数の積分について書いたときに、

$${x^n}$$の積分で$${n=-1}$$の場合は別に紹介すると書いたのはこの理由です。

ここで改めてまとめると、

$$
\int x^n dx = \frac{1}{n+1}x^{n+1}  \quad(n \ne ー1) \\ \int \frac{1}{x} dx = \log|x| +C 
$$

※$${\log x}$$及び、$${\log_{a}x}$$の積分に関しては、部分積分のときに紹介します。

まとめ

今回は、指数関数及び対数関数についてまとめました。

ここまでで、単一の関数やその微分積分について紹介してきましたが、
次回からは、これらを組み合わせた関数を微分したり積分したりする方法を紹介していきます。

#数学がすき #数学 #指数 #指数関数 #対数 #常用対数 #自然対数 #底 #真数 #対数関数 #ネイピア数 #e #微分 #積分 #mathematics #exponential #logarithm #log