２次対称群について

　これまでは、３次方程式を扱うために、３次対称群
　$${S_3=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}}$$
を主に扱ってきました。ここでは、３次対称群で辿ってきた道のりを、２次対称群（２次置換を要素とする集合）に当てはめてみます。
　後に２次方程式でガロアの証明を扱うための準備と、より簡単な２次という構造で、剰余群や巡回群を復習するのが目的です。
　最後のまとめで、２次対称群と３次対称群との関連をみていきます。

（復習）２次置換について

　まず２次置換について復習し、２次置換を要素とする集合が２次対称群になることを解説します。
　２次置換とは２つの文字の入れ替えです。２次置換には以下の２種類があります（本シリーズ (6)）。

$$
\begin{align*}
&➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}\\
\\
&➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha
\end{pmatrix}
=(\alpha     \beta)\\
\end{align*}
$$

　① は、$${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に置き換える置換です。つまり何も変化しない置換であり、これを恒等置換といいます。上から下へと文字を置き換えると読みます。
　② は、$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換です。これも、上から下へと文字を置き換えると読みます。
　これは $${\alpha}$$ と $${\beta}$$ の入れ換えなので、$${(\alpha     \beta)}$$ と互換で表示することができます（本シリーズ (8)）。
　また
　$${\alpha \rightarrow \beta \rightarrow \alpha \rightarrow \beta \rightarrow \alpha \rightarrow \cdots}$$
と巡回的に繰り返される置換なので、巡回置換となります。この巡回置換を
　$${(\alpha     \beta)}$$
と表記します（本シリーズ (14)）。
　２次方程式の２つの解を $${\alpha,  \beta}$$ とすると、その２つの解の入れ換えは２次置換になります。

　さて便宜的に、この２次巡回置換を次のように置きます。

$$
\begin{align*}
&➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}=id\\
\\
&➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha
\end{pmatrix}
=(\alpha     \beta)=\tau\\
\end{align*}
$$

　なお、何次であっても恒等置換は $${id}$$ と表記するとします。つまり３次置換だと
　$${id=\dbinom{\alpha     \beta     \gamma}{\alpha      \beta     \gamma}}$$
　４次置換だと
　$${id=\dbinom{\alpha     \beta     \gamma     \delta}{\alpha      \beta     \gamma     \delta}}$$
$${\hspace{26pt}\vdots}$$
　以下同様です。何も変化させないという役割は同じなので、特に誤解が生じない限り、恒等置換は同じ記号 $${id}$$ を用います。

２次対称群とは

　２次置換 $${id}$$ と $${\tau}$$ の集合
　$${\{id,  \tau\}}$$
は、置換の合成（積）という演算に関して群になります。
　この群を２次対称群といい、$${S_2}$$ という記号で表します。つまり
　$${S_2=\{id,  \tau\}}$$
　証明は本シリーズ (28)、(29) と同様なので割愛し、その要素同士について、合成（積）の演算表のみ記しておきます。

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & id & \underline{\tau}\\ \hline\hline
id & id & \tau\\ \hline
\underline{\tau} & \tau & \underline{id}
\end{array}
$$

　この演算表は、次の演算結果
　$${idid=id}$$
　$${id\tau=\tau}$$
　$${\tau id=\tau}$$
　$${\tau\tau=id}$$
を表にしたものです。
　さて、群である $${S_2}$$ は巡回群になります。以下、それについて証明していきます。　

２次対称群は巡回群であること

　$${S_2=\{id,  \tau\}}$$ の要素同士の置換の合成（積）の演算表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & id & \underline{\tau}\\ \hline\hline
id & id & \tau\\ \hline
\underline{\tau} & \tau & \underline{id}
\end{array}
$$

より
　$${\tau\tau=id}$$（下線部）
つまり
　$${\tau^2=id}$$
なので

$$
\begin{align*}
\{id,  \tau\}&=\{\tau^2,  \tau\}\\
&=\{\tau,  \tau^2\}
\end{align*}
$$

　よって、１つの要素 $${\tau}$$ だけを用いて表すことができたので、この群 $${\{id,  \tau\}}$$ は巡回群です。生成元が $${\tau}$$ なので、次のように表せます。

$$
\begin{align*}
\{id,  \tau\}&=\{\tau,  \tau^2\}\\
&=\langle\tau\rangle
\end{align*}
$$

　この群は、次のように $${id}$$ を最初に、次々と $${\tau}$$ を作用させていけば巡回的に現れる群です。

$$
\begin{align*}
&\hspace{1pt}id\\
&\downarrow  {\small \tau  を作用}\\
id\tau=&\hspace{3pt}\tau\\
&\downarrow  {\small \tau  を作用}\\
\tau\tau=&\hspace{1pt}id\\
&\downarrow  {\small \tau  を作用}\\
id\tau=&\hspace{3pt}\tau\\
&\downarrow  {\small 以下繰り返し}\\
&\hspace{4pt}\vdots
\end{align*}
$$

　円で描くと

　ちなみに、$${S_2=\{id,  \tau\}}$$ の要素同士の置換の合成（積）の演算表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & id & \tau\\ \hline\hline
id & id & \tau\\ \hline
\tau & \tau & id
\end{array}
$$

を、生成元 $${\tau}$$ だけで表すと次のようになります。

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
    & id & \tau\\ \hline\hline
id & \tau^2 & \tau\\ \hline
\tau & \tau & \tau^2
\end{array}
$$

　$${2\times2=4}$$ 通りのすべての結果は $${\tau}$$ のみで表されます。

巡回置換と巡回群を混同しないように

　巡回置換とは、先ほどやった２次置換

$$
\begin{align*}
&➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}\\
\\
&➁\hspace{6pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha
\end{pmatrix}
=(\alpha     \beta)\\
\end{align*}
$$

の $${➁}$$ のように、文字の入れ換えが循環する置換のことです。
　また巡回群とは、例えば $${➀}$$ と $${➁}$$ を要素とする群のことで、その要素が１つの文字で

$$
\begin{align*}
\{id,  \tau\}&=\{\tau,  \tau^2\}\\
&=\langle\tau\rangle
\end{align*}
$$

と表せる群のことです。巡回群 $${\{id,  \tau\}}$$ の要素の中に、巡回置換 $${\tau}$$ が含まれています。言葉が似ているので一応注意しておきます。

　ここで、$${S_2=\{id,  \tau\}}$$ の部分集合
　$${\phi}$$
　$${\{id\}}$$
　$${\{\tau\}}$$
　$${\{id,  \tau\}}$$
のうち、群は
　$${\{id\}}$$
　$${\{id,  \tau\}}$$
になりますが（自明な部分群）、これらはどちらも正規部分群（自明な正規部分群）になります。そのうち、自分自身ではない正規部分群 $${\{id\}}$$ について考え、それを
　$${I=\{id\}}$$
と置きます。
　そして、その $${I}$$ による左剰余類（および右剰余類）の集合が、巡回群になることを示します。方法は、本シリーズ (33) でやった方法とまったく同じですが、復習としてここでも示します。

I={id} による剰余類の集合が剰余群になること

　$${I=\{id\}}$$ による左剰余類とは、$${I}$$ に $${S_2=\{id,  \tau\}}$$ の要素 $${id,  \tau}$$ のすべてを左から作用させた
　$${idI,  \tau I}$$
のそれぞれを指します。
　同様に $${I}$$ による右剰余類とは、$${I}$$ に $${S_2}$$ の要素すべてを右から作用させた
　$${Iid,  I\tau}$$
のそれぞれを指します。
　まずは
　$${idI=Iid}$$
　$${\tau I=I\tau}$$
をすべて満たすことによって、$${I}$$ が正規部分群の定義を満たすことを確認します。
　なお、正規部分群の定義は次のものでした。

（復習）正規部分群の定義

　$${N}$$ を群 $${G}$$ の部分群とする。$${G}$$ のすべての要素 $${g}$$ について

$$
\begin{align*}
gN=Ng
\end{align*}
$$

を満たすとき、$${N}$$ を $${G}$$ の正規部分群という。

＊＊＊

　まず、２次対称群 $${S_2=\{id,  \tau\}}$$ の要素の置換の合成（積）の演算表

$$
\def\arraystretch{1.5}
\hspace{36pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & id & \tau\\ \hline\hline
id & id & \tau\\ \hline
\tau & \tau & id
\end{array}
$$

　より
　$${idid=id　\cdots (*1)}$$
　$${\tau id=\tau　\cdots (*2)}$$
　$${id\tau=\tau　\cdots (*3)}$$

(1a)　左から $${id}$$ を作用させる。

$$
\begin{align*}
idI&=id\{id\}\\
&=\{idid\}\\
&=\{id\}　\because  (*1)  より\\
\end{align*}
$$

(1b)　右から $${id}$$ を作用させる。

$$
\begin{align*}
Iid&=\{id\}id\\
&=\{idid\}\\
&=\{id\}　\because  (*1)  より\\
\end{align*}
$$

(1a)、(1b) より

$$
\begin{align*}
idI=Iid=\{id\}
\end{align*}
$$

(2a)　左から $${\tau}$$ を作用させる。

$$
\begin{align*}
\tau I&=\tau\{id\}\\
&=\{\tau id\}\\
&=\{\tau\}　\because  (*2)  より\\
\end{align*}
$$

(2b)　右から $${\tau}$$ を作用させる。

$$
\begin{align*}
I\tau&=\{id\}\tau\\
&=\{id\tau\}\\
&=\{\tau\}　\because  (*3)  より\\
\end{align*}
$$

(2a)、(2b) より

$$
\begin{align*}
\tau I=I\tau=\{\tau\}
\end{align*}
$$

　以上により
　$${idI=Iid}$$
　$${\tau I=I\tau}$$
をすべて満たすので、$${S_2}$$ の単位元だけからなる部分群 $${I=\{id\}}$$ は正規部分群であることが分かります。

 　すると、これにより、正規部分群 $${S_2}$$ を、２つの左剰余類
　$${idI=\{id\}}$$
　$${\tau I=\{\tau\}}$$
で類別することができます。

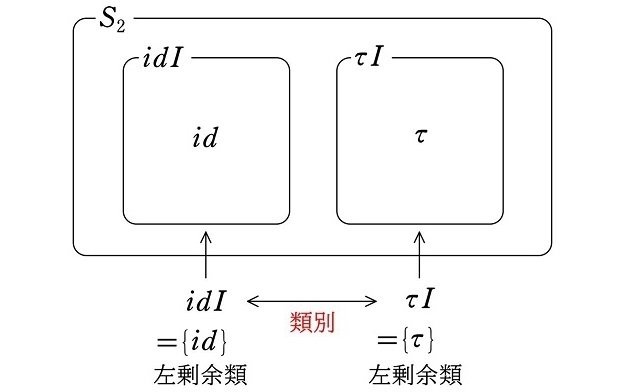
　さらに、$${S_2}$$ の正規部分群 $${I}$$ による左剰余類の集合
　$${\{idI,  \tau I\}}$$
は
　$${aI\circ bI\underset{def}{=}abI}$$
という演算に関して群（剰余群）になります。$${def}$$ は定義と言う意味です。

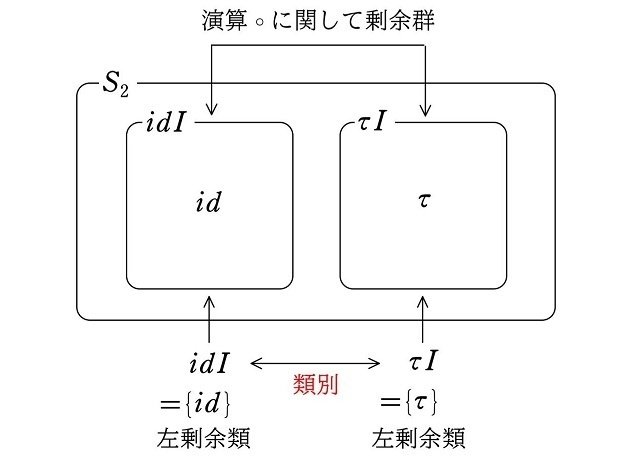
　証明は本シリーズ (31)、(32) と同様なので割愛し、演算表のみ記しておきます。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idI & \tau I\\ \hline\hline
idI & idI & \tau I\\ \hline
\tau I & \tau I & idI
\end{array}
$$

　この演算表は、次の演算結果
　$${idI \circ idI\underset{def}{=}ididI=idI}$$
　$${idI \circ \tau I\underset{def}{=}id\tau I=\tau I}$$
　$${\tau I \circ idI\underset{def}{=}\tau id I=\tau I}$$
　$${\tau I \circ \tau I\underset{def}{=}\tau\tau I=idI}$$
を表にしたものです。

「集合を要素とする集合」について

　左剰余類 $${idI}$$ と $${\tau I}$$ は
　$${idI=\{id\}}$$
　$${\tau I=\{\tau\}}$$
という集合なので、左剰余類の集合 $${\{idI,  \tau I\}}$$ は、次のような「集合を要素とする集合」であることに注意しておきます。

$$
\begin{align*}
\{\underset{集合が要素}{\underline{\{id\}},  \underline{\{\tau\}}}\}
\end{align*}
$$

　この集合の要素である、左剰余類という集合 $${\{idI\},  \{\tau I\}}$$ が
　$${aI\circ bI\underset{def}{=}abI}$$
という演算に関して剰余群になるということです。

$$
\begin{align*}
&\hspace{14pt}\underline{\footnotesize \hspace{0.2pt}剰余群\hspace{0.2pt}}\\[-7pt]
&\hspace{9pt}\downarrow\hspace{19pt}\downarrow\\[-3pt]
&\{\underset{idI}{\underline{\{id\}}},  \underset{\tau I}{\underline{\{\tau\}}}\}
\end{align*}
$$

　なお、同様の議論によって右剰余類の集合
　$${\{Iid,  I\tau\}}$$
も
　$${Ia\circ Ib\underset{def}{=}Iab}$$
という演算に関して剰余群になります。演算表のみ記しておきます。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & Iid & I\tau\\ \hline\hline
Iid & Iid & I\tau\\ \hline
I\tau & I\tau & Iid
\end{array}
$$

I={id} による剰余類の集合が巡回群になること

　２次対称群 $${S_2=\{id,  \tau\}}$$ の正規部分群 $${I=\{id\}}$$ による左剰余類の集合 $${\{id I,  \tau I\}}$$ は、剰余群であると同時に巡回群でもあります。

　以下、それについて証明します。最初にやった、２次対称群 $${S_2=\{id,  \tau\}}$$ が巡回群であることと、証明の方法はまったく同じです。

$$
\begin{align*}
S_2=\{id,  \tau\}  &は\bm{巡回群}  {\small \leftarrow  すでに証明}\\
&\updownarrow  {\small 証明の方法は同じ}\\
\{id I,  \tau I\}  &は\bm{巡回群}  {\small \leftarrow  今から証明}
\end{align*}
$$

　次の $${\{id I,  \tau I\}}$$ の要素同士の積の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idI & \underline{\tau I}\\ \hline\hline
idI & idI & \tau I\\ \hline
\underline{\tau I} & \tau I & \underline{idI}
\end{array}
$$

　より
　$${\tau I  \tau I=id I}$$（下線部）
つまり
　$${{(\tau I)}^2=id I}$$
なので

$$
\begin{align*}
\{id I,  \tau I\}&=\{{(\tau I)}^2,  \tau I\}\\
&=\{\tau I,  {(\tau I)}^2\}
\end{align*}
$$

　よって、１つの要素 $${\tau I}$$ だけを用いて表すことができたので、この剰余群は巡回群です。生成元が $${\tau I}$$ なので、次のように表せます。

$$
\begin{align*}
\{id I,  \tau I\}&=\{\tau I,  {(\tau I)}^2\}\\
&=\langle\tau I\rangle
\end{align*}
$$

　この群は、次のように $${idI}$$ を最初に、次々と $${\tau I}$$ を作用させていけば巡回的に現れる群です。

$$
\begin{align*}
&\hspace{2pt}idI\\
&\hspace{1pt}\downarrow  {\small \tau I  を作用}\\
idI\tau I=&\hspace{1pt}\tau I\\
&\hspace{1pt}\downarrow  {\small \tau I  を作用}\\
\tau I\tau I=&\hspace{2pt}idI\\
&\hspace{1pt}\downarrow  {\small \tau I  を作用}\\
id I\tau I=&\hspace{1pt}\tau I\\
&\hspace{1pt}\downarrow  {\small 以下繰り返し}\\
&\hspace{4pt}\vdots
\end{align*}
$$

　つまり

　円で描くと

　ちなみに、$${\{id I,  \tau I\}}$$ の要素同士の置換の合成（積）の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & id I & \tau I\\ \hline\hline
id I & id I & \tau I\\ \hline
\tau I & \tau I & id I
\end{array}
$$

を、生成元 $${\tau I}$$ だけで表すと次のようになります。

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
    & id & \tau\\ \hline\hline
id I & {(\tau I)}^2 & \tau I\\ \hline
\tau I & \tau I & {(\tau I)}^2
\end{array}
$$

　$${2\times2=4}$$ 通りのすべての結果は $${\tau I}$$ のみで表されます。

まとめ

　本記事でやったことを「正規部分群の縮小」の流れ図によって復習すると、次のようになります。

$$
\begin{align*}
S_2&=\{id,  \tau\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-34pt}正規部分群  I=\{id\} による \atop \hspace{0pt}\bm{巡回群}  \{id I,  \tau I\}=\langle\tau I\rangle  が構成可能}\\[12pt]
I&=\{id\}  は  S_2  の\bm{正規部分群}
\end{align*}
$$

　なお、$${S_2}$$ が巡回群であることは本質的ではなく、$${I}$$ が $${S_2}$$ の正規部分群であり、かつ $${S_2}$$ の $${I}$$ による剰余群が巡回群になることが重要です。
　ここで、$${S_2}$$ の正規部分群の縮小の列は

$$
\begin{align*}
S_2\hspace{4pt}&\overset{縮小}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI,  \tau I\} \atop が巡回群}
\end{align*}
$$

　これを本シリーズ (33) でやった、３次対称群 $${S_3}$$ の「正規部分群の縮小」の流れ図と比較してみましょう。$${S_3}$$ については次のようになります。

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-15pt}正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{0pt}\bm{巡回群}  \{idN,  \tau_1N\}
=\langle\tau_1N\rangle  が構成可能}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}  は  S_3  の\bm{正規部分群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-58pt}正規部分群  I=\{id\}  による \atop \bm{巡回群}  \{idI,  \rho_2I,  \rho_3I\}=\langle\rho_2I\rangle  が構成可能}\\[12pt]
I&=\{id\}  は  N  の\bm{正規部分群}
\end{align*}
$$

　$${S_3}$$ の正規部分群の縮小の列は　

$$
\begin{align*}
&S_3\hspace{4pt}\overset{縮小}{\supset}\hspace{-8pt}\underset{\tiny S_3 の正規部分群}{N}\hspace{-8pt}\overset{縮小}{\supset}\hspace{-8pt}\underset{\tiny N の正規部分群}{I}\\[-4pt]
&\hspace{18pt}\uparrow\hspace{37pt}\uparrow\\[-2pt]
&\hspace{-4pt}{\footnotesize \{idN,  \tau_1N\} \atop が巡回群}\hspace{2pt}{\footnotesize \{idI,  \rho_2I,  \rho_3I\} \atop が巡回群}
\end{align*}
$$

となります。先ほどやった２次対称群 $${S_2}$$ の正規部分群の縮小の列は

$$
\begin{align*}
S_2\hspace{4pt}&\overset{縮小}{\supset}\hspace{-8pt}\underset{\tiny S_2 の正規部分群}{I}\\[-4pt]
&\hspace{4pt}\uparrow\\[-2pt]
&\hspace{-10pt}{\footnotesize \{idI,  \tau I\} \atop が巡回群}
\end{align*}
$$

であったので、どちらも $${I=\{id\}}$$ にまで縮小されていることが分かります。

　まとめると、
　$${➀}$$ 正規部分群を取りながら群が縮小すること
　$${➁}$$ その正規部分群による剰余類の集合が巡回群になること
の２つの関係を保持しながら、単位元のみからなる正規部分群 $${\{id\}}$$ にうまくたどり着くことができれば、その方程式には解の公式が存在する。逆に $${\{id\}}$$ にたどり着かなければ、解の公式は存在しない、というのがガロアのアイデアです。

２次対称群と３次対称群に見られる同じ構造

　実は、２次対称群 $${S_2=\{id,  \tau\}}$$ の正規部分群 $${I=\{id\}}$$ による左剰余類の集合
　$${\{id I,  \tau I\}=\{\tau I,  {(\tau I)}^2\}=\langle\tau I\rangle}$$
が巡回群になる構造は、本シリーズ (33) でやった、３次対称群 $${S_3}$$ の正規部分群 $${N=\{id,  \rho_2,  \rho_3\}}$$ による左剰余類の集合
　$${\{idN,  \tau_1N\}=\{\tau_1N,  (\tau_1N)^2\}=\langle\tau_1N\rangle}$$
が巡回群になる構造と、同じ構造になっていることに気付きます。

●  $${\{id I,  \tau I\}=\{\tau I,  {(\tau I)}^2\}=\langle\tau I\rangle}$$ の演算表

$$
\def\arraystretch{1.5}
\hspace{41pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
    & id & \tau\\ \hline\hline
id I & {(\tau I)}^2 & \tau I\\ \hline
\tau I & \tau I & {(\tau I)}^2
\end{array}
$$

$${\hspace{65pt}\updownarrow}$$ 同じ構造

●  $${\{idN,  \tau_1N\}=\{\tau_1N,  (\tau_1N)^2\}=\langle\tau_1N\rangle}$$ の演算表

$$
\def\arraystretch{1.5}
\hspace{45pt}後\\
\raisebox{-10pt}{先}\hspace{4pt}
\begin{array}{c||c|c}
\circ & idN & \tau_1N\\ \hline\hline
idN & (\tau_1N)^2 & \tau_1N\\ \hline
\tau_1N & \tau_1N & (\tau_1N)^2
\end{array}
$$

　つまり
　$${\{id I,  \tau I\}=\{\tau I,  {(\tau I)}^2\}=\langle\tau I\rangle}$$
も
　$${\{idN,  \tau_1N\}=\{\tau_1N,  (\tau_1N)^2\}=\langle\tau_1N\rangle}$$
も、どちらも２次の（２変数の）巡回群となります。
　これについて「正規部分群の縮小」の流れ図で確認すると下線部のところです。剰余群を構成する最初のステップで、その剰余群はどちらも２次の（２変数の）巡回群となります。

●  $${\{id I,  \tau I\}=\{\tau I,  {(\tau I)}^2\}=\langle\tau I\rangle}$$ の場合

$$
\begin{align*}
S_2&=\{id,  \tau\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-34pt}正規部分群  I=\{id\} による \atop \hspace{0pt}\underset{\bm{２変数の巡回群}}{\underline{\bm{巡回群}  \{id I,  \tau I\}=\langle\tau I\rangle  が構成可能}}}\\[12pt]
I&=\{id\}  は  S_2  の\bm{正規部分群}
\end{align*}
$$

●  $${\{idN,  \tau_1N\}=\{\tau_1N,  (\tau_1N)^2\}=\langle\tau_1N\rangle}$$ の場合

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-15pt}正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{0pt}\underset{\bm{２変数の巡回群}}{\underline{\bm{巡回群}  \{idN,  \tau_1N\}=\langle\tau_1N\rangle  が構成可能}}}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}  は  S_3  の\bm{正規部分群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-58pt}正規部分群  I=\{id\}  による \atop \bm{巡回群}  \{idI,  \rho_2I,  \rho_3I\}=\langle\rho_2I\rangle  が構成可能}\\[12pt]
I&=\{id\}  は  N  の\bm{正規部分群}
\end{align*}
$$

　これは、平方根 $${\sqrt{\hspace{10pt}}}$$ の添加と関係があります。平方根は２乗恨のことです。２乗恨と２次の巡回群は「２」というキーワードで関係しています。
　ここでは簡単に述べますが、２次方程式の解の公式の導出には平方根 $${\sqrt{\hspace{10pt}}}$$ が必要です（下線部）（本シリーズ (1)、(5)、(22)）。

＜２次方程式の解の公式＞

　２次方程式 $${ax^2+bx+c=0}$$ について

$$
\begin{align*}
x=\dfrac{-b\pm\underline{\sqrt{b^2-4ac}}}{2a}
\end{align*}
$$

　本質的には

$$
\begin{align*}
〇^2=\square　より　〇=\pm\sqrt{\square}
\end{align*}
$$

という「平方根を取る操作」が入ります。

　つまり、２次方程式 $${ax^2+bx+c=0}$$ の解の公式は、その係数 $${a,  b,  c}$$ の加減乗除という操作だけでは構成できず、平方根の添加、つまり「平方根を取るという操作を仲間に加えること」が必要になります（本シリーズ (11)、(18)）（注１）。
　３次方程式の解の公式の導出においては、最初に２次方程式の解の公式を利用します（本シリーズ (3)、(12)、(25)）。２次方程式の解の公式を使うので、やはり平方根が必要です。平方根は３乗根の中に現れます（下線部）。

＜３次方程式の解の公式＞

　３次方程式 $${ax^3+bx^2+cx+d=0}$$ について

$$
x=
\begin{cases}
-\dfrac{b}{3a}+\sqrt[3]{-\dfrac{q}{2}+\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}}+\sqrt[3]{-\dfrac{q}{2}-\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}}\\[10pt]
-\dfrac{b}{3a}+\omega\sqrt[3]{-\dfrac{q}{2}+\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}}+\omega^2\sqrt[3]{-\dfrac{q}{2}-\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}}\\[10pt]
-\dfrac{b}{3a}+\omega^2\sqrt[3]{-\dfrac{q}{2}+\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}}+\omega\sqrt[3]{-\dfrac{q}{2}-\underline{\sqrt{\left(\dfrac{q}{2}\right)^2+\left(\dfrac{p}{3}\right)^3}}}
\end{cases}
$$

ただし

$$
\begin{align*}
p&=-\frac{1}{3}\left(\frac{b}{a}\right)^{2}+\frac{c}{a}\\
q&=\frac{2}{27}\left(\frac{b}{a}\right)^{3}-\frac{1}{3}\left(\frac{b}{a}\right)\left(\frac{c}{a}\right)+\frac{d}{a}
\end{align*}
$$

　数学では、同じ構造をもつものを”同一視”して考えます。
　つまり、「２次の巡回群の構成」という構造を同一視することによって、２次方程式においても３次方程式においても、「平方根の添加」という共通の性質を導きだすことができます。

●  $${\{id I,  \tau I\}=\{\tau I,  {(\tau I)}^2\}=\langle\tau I\rangle}$$ の場合

$$
\begin{align*}
S_2&=\{id,  \tau\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-34pt}正規部分群  I=\{id\} による \atop \hspace{0pt}\underset{\footnotesize \bm{平方根の添加}}{\underline{\bm{巡回群}  \{id I,  \tau I\}=\langle\tau I\rangle  が構成可能}}}\\[12pt]
I&=\{id\}  は  S_2  の\bm{正規部分群}
\end{align*}
$$

●  $${\{idN,  \tau_1N\}=\{\tau_1N,  (\tau_1N)^2\}=\langle\tau_1N\rangle}$$ の場合

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-15pt}正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{0pt}\underset{\footnotesize \bm{平方根の添加}}{\underline{\bm{巡回群}  \{idN,  \tau_1N\}=\langle\tau_1N\rangle  が構成可能}}}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}  は  S_3  の\bm{正規部分群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-58pt}正規部分群  I=\{id\}  による \atop \bm{巡回群}  \{idI,  \rho_2I,  \rho_3I\}=\langle\rho_2I\rangle  が構成可能}\\[12pt]
I&=\{id\}  は  N  の\bm{正規部分群}
\end{align*}
$$

　なお、やや先走りとなりますが、３次方程式の解の公式の導出において、巡回群 $${\{idI,  \rho_2I,  \rho_3I\}}$$ が構成できることは、３乗根 $${\sqrt[3]{\hspace{10pt}}}$$ の添加と関係があります（本シリーズ (13)、(18) 他）。

$$
\begin{align*}
S_3&=\{id,  \rho_2,  \rho_3,  \tau_1,  \tau_2,  \tau_3\}  は\bm{群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-15pt}正規部分群  N=\{id,  \rho_2,  \rho_3\}  による \atop \hspace{0pt}\underset{\footnotesize \bm{平方根の添加}}{\underline{\bm{巡回群}  \{idN,  \tau_1N\}=\langle\tau_1N\rangle  が構成可能}}}\\[12pt]
N&=\{id,  \rho_2,  \rho_3\}  は  S_3  の\bm{正規部分群}\\[10pt]
\bm{縮小}  &\downarrow  {\small \hspace{-58pt}正規部分群  I=\{id\}  による \atop \underset{\footnotesize \bm{３乗根の添加}}{\underline{\bm{巡回群}  \{idI,  \rho_2I,  \rho_3I\}=\langle\rho_2I\rangle  が構成可能}}}\\[12pt]
I&=\{id\}  は  N  の\bm{正規部分群}
\end{align*}
$$

　本質的には

$$
\begin{align*}
〇^3=\square　より　〇=\sqrt[3]{\square},   \omega\sqrt[3]{\square},   \omega^2\sqrt[3]{\square}
\end{align*}
$$

という「３乗根を取る操作」が入ります。以上の内容について、次の章から解説していきます。

（コメント）

　ここから先は、どう書いていけばいいのか非常に難しくなってきました。
　大学の専門書だとかなり抽象的であり、ガロアの原論分も今の視点で見れば分かりにくい部分も多いので、それを具体的なレベルまでどう落とせばいいのか考慮中です。

（注１）

　これまでは、平方根の添加について「平方根を仲間に加える」というニュアンスで書いてきたかもしれません。
　当然平方根なら何でもよいわけではなく、解の公式の構成にあたって（加減乗除という操作の他に）必要な式の平方根を取る必要があるので、ここでは
「平方根を取るという操作を仲間に加える」
という表現にしました。これなら、解の公式を求める（解を求める）にあたって、必要な式（数）の平方根を取ることができます。
　結果的に
「必要な平方根が加減乗除の仲間に加えられる」
ことで解の公式は構成可能となるので、大きな誤解を与えず同じ意味として伝わってくれればと考えています。
　これで十分なのかどうか分かりませんが、この辺りの言葉の曖昧さについて、全面的に手直しするかもしれません。

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について簡単に解説
（29）中学でも分かるガロアの証明②　ガロアの発見した「部分群」について簡単に解説
（30）中学でも分かるガロアの証明③　ガロアの発見した「正規部分群」について
（31）中学でも分かるガロアの証明➃　正規部分群による剰余類の集合が群（剰余群）になること
（32）中学でも分かるガロアの証明⑤　単位元のみの正規部分群 $${\{id\}}$$ による剰余類の集合が群（剰余群）になること
（33）中学でも分かるガロアの証明⑥　巡回群について、および剰余群が巡回群になること