「本当に」日本一マクドナルドから遠い場所
こんにちは、本業の稼働が 100% フロントエンドになっちゃっていてそろそろデータをいじりたいヌノカワです。
先日、qiita で日本一マクドナルドから遠い場所という記事を見つけて読んでみたんですが、探索する過程が意外とアナログなところも含めて面白かったです。
ただ、800 を超えるいいねをもらってるのを見て、謎のジェラシーと対抗心が生まれ、地理空間演算で「本当に」日本一マクドナルドから遠い場所を突き止めてみようというのが主旨です。
qiita の当記事では、マクドナルドの地点からバッファー (地点を中心とした円) を生成して徐々に半径を広げ、かすかに残っている陸地を (目視で!) 絞って行くというハートウォーミングな内容です。そこをもう少し論理的に探索してみましょう。
私が考えたアプローチはこんな感じでございます。
1. マクドナルドの地点を母点としたボロノイ図を生成する
2. ボロノイ領域と母点を関連づける
3. ボロノイ図を日本の海岸線ポリゴンでインターセクトする (=くり抜く)
4. インターセクト後の多角形の各頂点と母点の距離を算出する
5. 距離の最大値を算出する
アプローチの詳細
ボロノイ図ってなんやねんという人はググってください。『なわばりの数理モデル』はオススメです。細かい内容は忘れましたが。
ボロノイ図は隣接する 2 点間の垂直二等分線によってできており、その領域内の地点は母点が最寄りであるということになります。領域の中でもっとも離れている地点は領域を表す多角形の頂点のいずれかになります。
したがって、多角形の頂点と母点の距離さえ算出すれば、その最大値が日本の中でもっともマクドナルド (母点) から離れた場所 (頂点) がわかります。
ただし、問題は「日本の中で」ということは陸地を表しているでしょうから、海岸線ではみ出た領域は除かなければなりません。よって、そのはみ出た多角形の面は海岸線に置換する必要があります。
それは、ボロノイ図を日本の海岸線でくり抜いた図形が作れれば良いので、GIS (Geographic Information System) のインターセクトという処理で実現できます。
なんかわけわからんという人はこの後をぜひ読んでください。ビジュアルで確認しながら進めるので、直感的に理解できると思います。
実践 - JavaScript でやってみた
え?なぜ JavaScript?Python とか R じゃないん??という声が聞こえてきそうですが、一度本気で使い倒してみたかった turf.js という空間演算ライブラリを使ってどこまでやれるか試したいというのがモチベーションです。
基本的な演算処理系はほとんどメソッドが用意されているので、サクッとやりたい時にはとっつきやすくてオススメです。
0. マクドナルドの地点情報を拝借する
まずはマクドナルドの地点データが必要です。
qiita の記事では、マクドナルドのサイトをハックしてレスポンスの JSON を抜き出しているようですが、全く同じように抜き出させていただきました。もし怒られたらこの記事ごと抹消してビッグマック買ってきます。
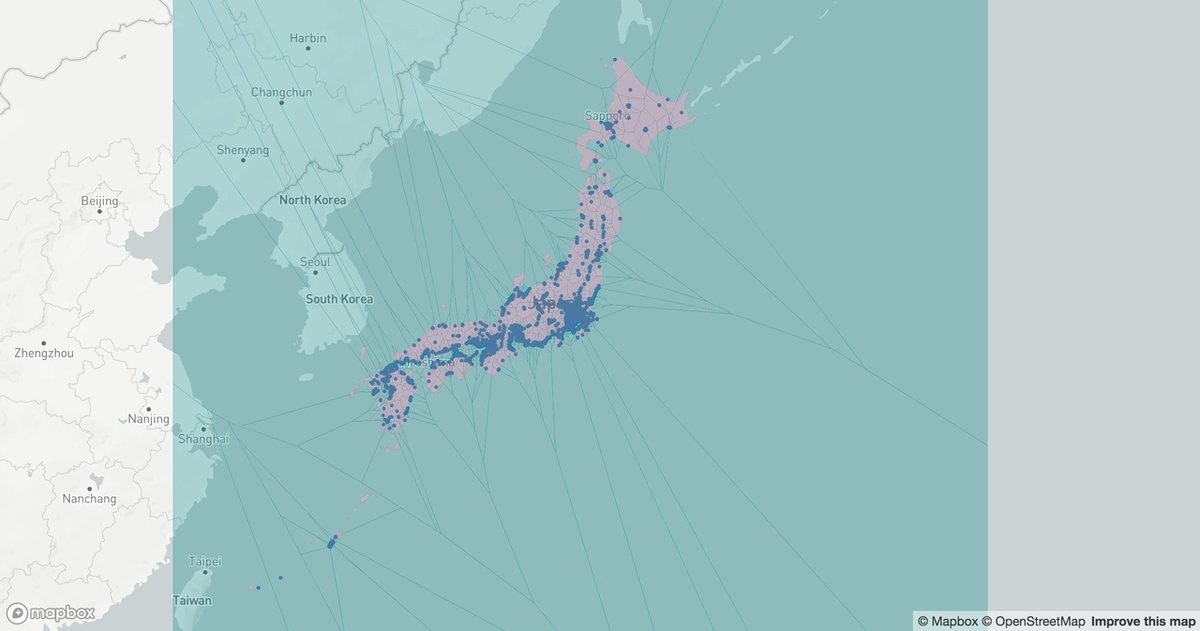
地図にプロットするとこんな感じ。
地図は Mapbox GL JS というライブラリを使っています。なんでかというと、今回はマクドナルドの地点だけで 2887 件あり、かつ、それを母店にしたボロノイ図形と海岸線を描画したいので、WebGL (Canvas) じゃないとかなり描画パフォーマンスがしんどいというのと、単純にこのライブラリが大好きだからです。
1. マクドナルドの地点を母点としたボロノイ図を生成する (turf.voronoi)
ボロノイ図の生成は turf.js の turf.voronoi というメソッドを使用します。
マクドナルド地点の配列からボロノイを生成するコードはこんな感じで書けます。カンタン。
// get the macdonald json
d3.json(macdonaldsJsonURL, (err, res) => {
// array of macdonald points
const mdPoints = res.map(d => turf.point([d.longitude, d.latitude], { name: d.name }));
// generate voronoi
const macdonalds = turf.featureCollection(mdPoints);
const voronoi = turf.voronoi(macdonalds, { bbox: [120, 20, 160, 50] });
});地図にボロノイを表示してみる。
関東に寄ってみるとこんな感じ。
2. ボロノイ領域と母点を関連づける (turf.booleanPointInPolygon)
4. インターセクト後の多角形の各頂点と母点の距離を算出する
を行うには、各ボロノイ領域 (ポリゴン) がどの母点によるものかを知る必要があります。そこで、母点とボロノイ領域を ID で関連づけたいんですが、turf.voronoi では母点のプロパティをボロノイに継承する的なオプションがない模様 (ソースまで見ました)。
詰んだ。
と一瞬思ったけど、turf.js を使い倒すという使命感もあるので、各母点と (空間的位置関係が) 重なる図形にプロパティを継承するというのをやってみます。
turf.booleanPointInPolygon を使えば、指定したポイントがポリゴンに含まれているかを判定できるので、以下のようなコードで、ボロノイ領域に含まれる点 (=母点) の id をボロノイ領域ポリゴンにも割り当てます。
const relatedVoronoi = [];
voronoi.forEach(v => {
mdPoints.features.forEach(m => {
if (turf.booleanPointInPolygon(m, v)) {
// assign a mcdonald id to a voronoi
v.properties.mid = m.properties.id;
relatedVoronoi.push(v);
}
});
});これでボロノイの mid を見れば、どのポイントが母点かを判別できるようになりました。
3. ボロノイ図を日本の海岸線ポリゴンでインターセクトする (turf.intersect)
ボロノイ図はこのままだと、海上まで広がってしまってます。これを日本の陸地内にくり抜く必要があります。
これは turf.intersect を使います。二つの異なるポリゴンを引数に指定すると、重なった部分のポリゴンを返してくれます。
const intersectedVoronoi = [];
voronoi.forEach(v => {
japanBorder.geometry.coordinates.forEach(b => {
// get the intersection with a voronoi and boundaries
const intersection = turf.intersect(turf.polygon(b), v);
if (intersection && intersection.properties) {
intersection.properties.mid = v.properties.mid;
intersectedVoronoi.push(intersection);
}
});
});結果はこんな感じ。綺麗に日本の陸地境界線でくり抜かれてますね。
関東に寄ってみるとよくわかります。
4. インターセクト後の多角形の各頂点と母点の距離を算出する
ここまで来るといよいよって感じがしますね。ワクワクしますね。
あとはボロノイ領域の各頂点と母点の距離をひたすら算出するだけです。距離の算出は turf.distance を使います。
let maxDistance = 0;
let maxDistanceLine = {};
let md = '';
voronoi.forEach(v => {
mdPoints.features.forEach(m => {
if (v.properties.mid === m.properties.id) {
v.geometry.coordinates[0].forEach(c => {
if (Array.isArray(c) && c.length === 2) {
const from = m;
const to = turf.point(c);
// get the distance between generatrix and vertex
const distance = turf.distance(from, to);
if (maxDistance < distance) {
maxDistance = distance;
maxDistanceLine = turf.lineString([m.geometry.coordinates, c]);
md = m.properties.name;
}
}
});
}
});コード見ればわかると思いますが、最大値も合わせて求めちゃってます。というわけで、次でいよいよ答えあわせ!!
5. 距離の最大値を算出する
先に最大値を算出する際に、日本一マクドナルドから遠い場所とそこから最寄りのマクドナルドの間で線を引くように準備をしていました。
これを描画すると…
!!!!????
あ、あれ…
あ、そうか。
離島入ってるんだもん。そうなるよねー…
オリジナルの日本一マクドナルドから遠い場所を読み返すと、
注) 離島は除きます。離島を含めると南鳥島がぶっちぎりです。
って書いてあるし!!!!
というかちょっと考えればわかるだろう!自分アホ!!と叫びました。
いよいよ詰んだか…離島だけを除く処理って…と思って途方にくれていましたが、ありましたよ。簡単に離島を除く方法。
延長戦!日本の陸地ポリゴンから離島を取り除く (turf.area)
そう、面積で絞り込めばいいんじゃん。簡単でしたね。かなり動揺してました。
面積の算出は turf.area でできるので、沖縄の面積 (=約2200㎢) より小さいポリゴンは弾いてみて、ここまで書いてきた処理を再実行してみます。
結果は…
おお!
おおお!!!
北海道最西端・せたな町 尾花岬ではない!!!
日本一マクドナルドから遠い場所は襟裳岬でした!!!!
ちなみに距離は 107.057km、最寄り店舗は「帯広イトーヨーカドー店」でした。
陸地境界線は若干頂点が間引いて単純化されているので、多少誤差はあるかもしれないですが、距離が明らかに勝っています。
をやっていた @330k さんにもう一度検証して欲しい。
長くなりましたが、久しぶりに無駄なデータサイエンス力を発揮できて楽しかった。そして、ここまでできる turf.js すごい。
最後まで読んでくださってありがとうございました。また面白いテーマを見つけたら note に書いてみようと思います〜。
[追記]
その後、オリジナル日本一マクドナルドから遠い場所の投稿者である @j_catfish さんが検証してくださいました。結果、陸地境界線付近では隣接すべき2点間でボロノイ線がうまく引けてないケースがあることがわかり、しかもドヤ顔で導出した新解答も誤りであることが発覚しました。無念…
というわけで、(本当の) 日本一はやっぱり「尾花岬」でございました。お騒がせいたしました。
こうやって、相互に検証し合うのもデータサイエンスの醍醐味ですかね!アプローチ間違ってないし!(言い訳)
時間が許せば不完全だったボロノイの原因究明をしたい。