こんにちは。Junです。

前回は、多項式関数の微分積分について書きましたが、今回はその他の関数の微分積分について書いていきたいと思います。

その前に、多項式関数以外の関数の概要について書き、その後、その関数の微分積分について書いていこうと思います。

今回は、三角比・三角関数と、その極限、微分積分について書いていきます。

前回までのnoteをご覧になっていない方は、以下を先にご参照ください。

⒈ 三角比

三角関数に入る前に、三角比について書いていきます。

i. 直角三角形による三角比の定義

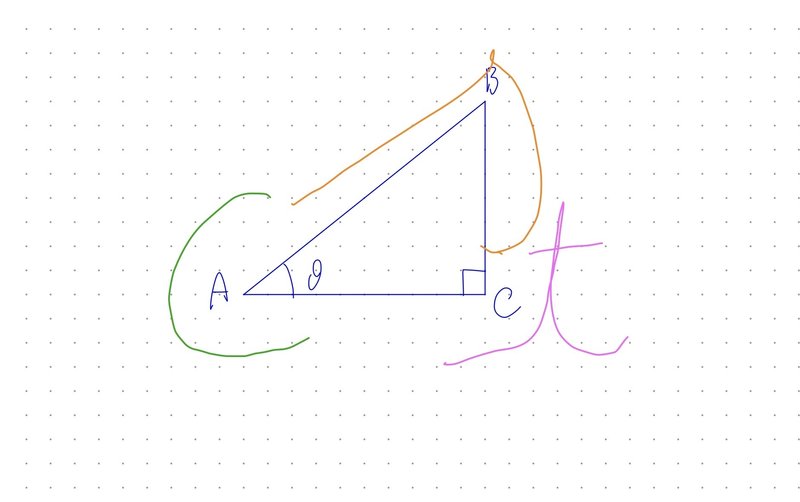
$$
\sin \theta = \frac{BC}{AB}
$$

$$
\cos \theta =\frac{AC}{AB}
$$

$$
\tan \theta = \frac{BC}{AC}
$$

ii. 単位円による三角比の定義

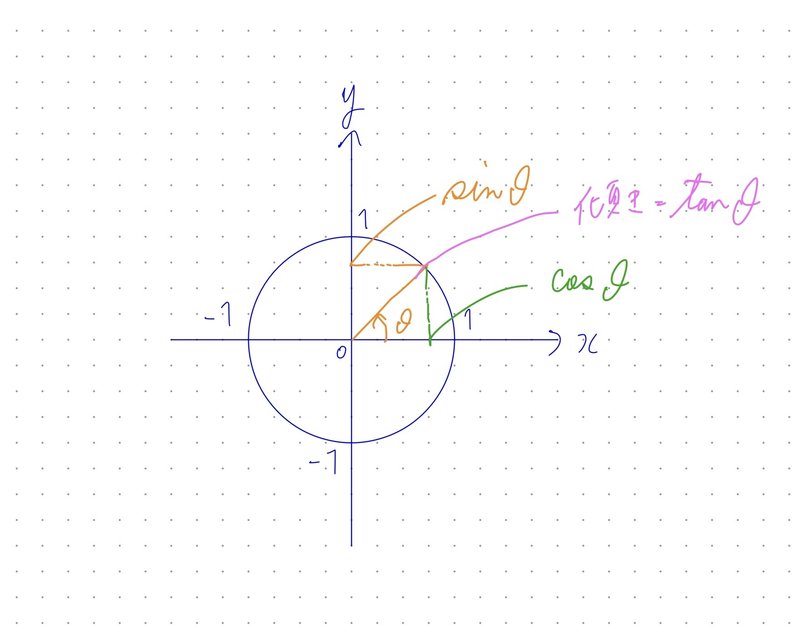
$${\sin \theta}$$は$${y}$$軸、$${\cos \theta}$$は$${x}$$軸、$${\tan \theta}$$は、傾きと定義します。

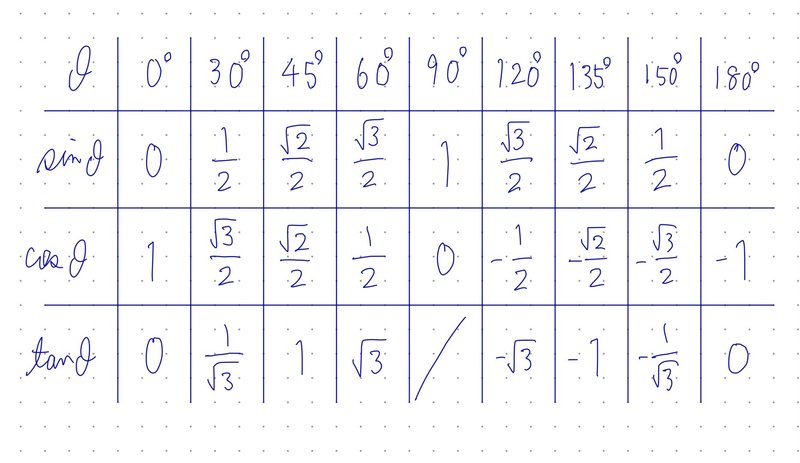
iii. 覚えておくべき三角比の値

角には様々な値があり、すべての角の三角比の値を覚えておく必要はありませんが、以下に示す角の三角比は覚えておく必要があります。

iv. 三角比の性質

三角比には以下のような性質があります。

$$
\sin ^2 \theta + \cos ^2 \theta = 1 \dots (*)
$$

単位円の方程式$${x^2+y^2=1}$$に、$${x=\cos \theta}$$、$${y=\sin \theta}$$を代入すれば導けます。

$$
\tan \theta = \frac{\cos \theta}{\sin \theta}\dots (**)
$$

単位円による$${\tan \theta}$$の定義から、導かれます。

$$
1+\tan ^2 \theta=\frac{1}{\cos ^2 \theta}
$$

$${(*)}$$の式を変形すると、

$$
\frac{\sin ^2 \theta}{\cos ^2 \theta}+1=\frac{1}{cos^2 \theta}
$$

$${(**)}$$より、

$$
\tan^2 \theta + 1 = \frac{1}{cos^2 \theta}
$$

が導かれます。

v. 正弦定理

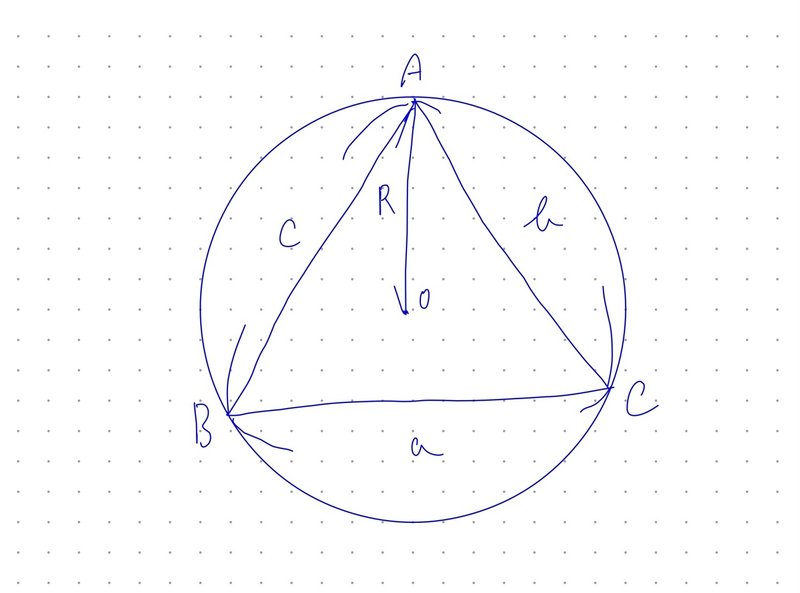
上図のような$${\triangle ABC}$$と外接円があり、外接円の半径をRとすると、

$$
\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} = 2R
$$

が成り立ちます。

なお、この定理は使用頻度があまり高くないため、証明は省略します。

vi. 余弦定理

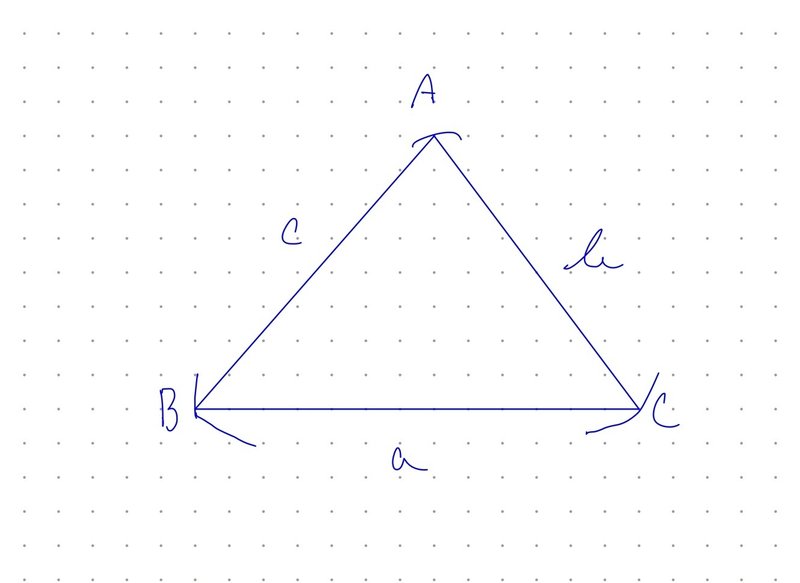
上図のような$${\triangle ABC}$$があるとき、以下が成り立ちます。

$$
a^2 = b^2 + c^2 -2bc \cos A
$$

$$
b^2 = c^2 + a^2 -2ca \cos B
$$

$$
c^2 = a^2 + b^2 -2ab \cos C
$$

あるいは、これらを変形して、

$$
\cos A = \frac{b^2+c^2-a^2}{2bc}
$$

$$
\cos B = \frac{c^2+a^2-b^2}{2ca}
$$

$$
\cos C = \frac{a^2+b^2-c^2}{2ab}
$$

の形でもよく用いられます。

この定理の証明は以下をご参照ください。

vii. 三角形の面積（sinを用いる方法）

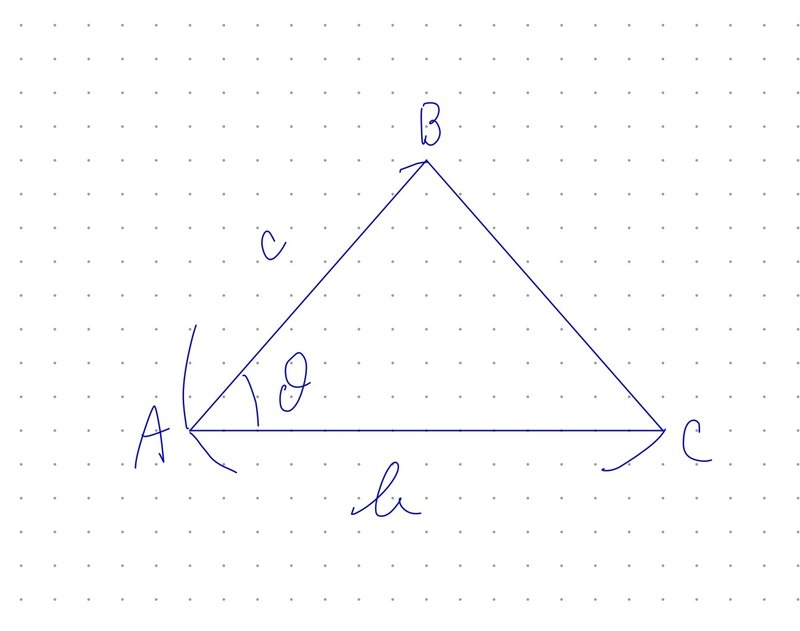
上図のように、2辺と、それに挟まれる角がわかっているとき、$${\triangle ABC}$$の面積Sは、

$$
S=\frac{1}{2}bc\sin \theta
$$

で求まります。

【証】

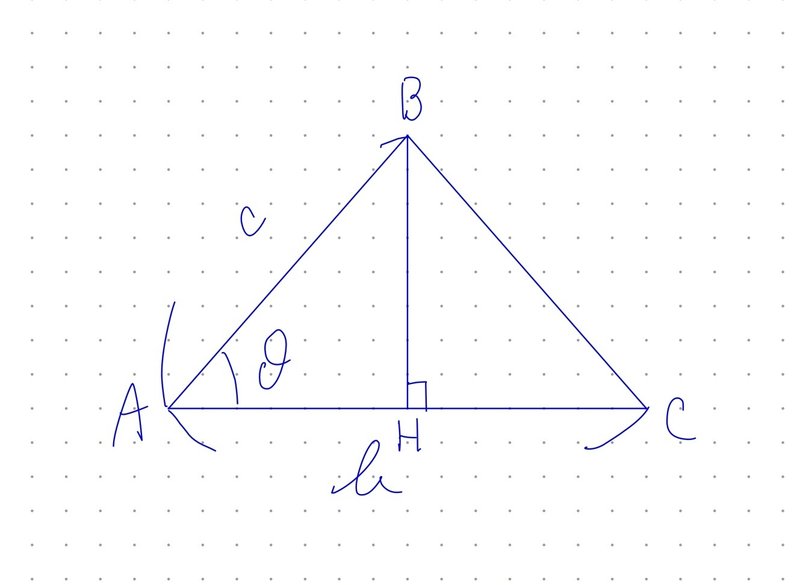
上図のように取ると、

$$
S=\frac{1}{2}AC\cdot BH=\frac{1}{2}bBH
$$

（底辺×高さ÷2）

$$
\sin A = \frac{BH}{c}
$$

より、

$$
BH=c\sin A
$$

これらより、

$$
S=\frac{1}{2}bc\sin A
$$

⒉ 三角関数

ここからは、この三角比を関数として扱っていきます。その前に、今後の話を進めていくにあたって、定義しておくことがあります。

i. 弧度法と度数法

これまでは、$${30^\circ, 60^\circ}$$などで表現してきました。この表現方法のことを、度数法と言います。

この度数法は、三角関数になると、使い勝手があまり良くないので、ここで新たな角の表現法を導入します。

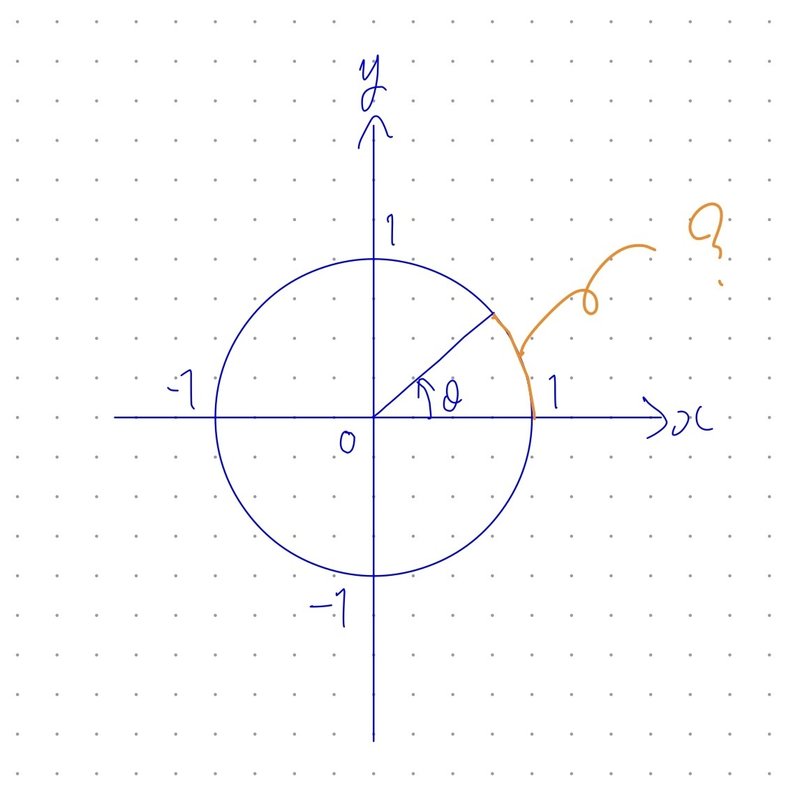
今までは、度数法で表現してきたものを、「単位円における$${\theta ^\circ}$$」の時の弧の長さ」で定義することにします。この角の表現法を弧度法と言います。

$${180^\circ}$$の時の、弧の長さは$${2\pi \frac{1}{2}=\pi}$$なので、
$${180^\circ = \pi (rad)}$$となります。（単位はラジアンと読みます）

有名角の弧度法は以下のようになります。

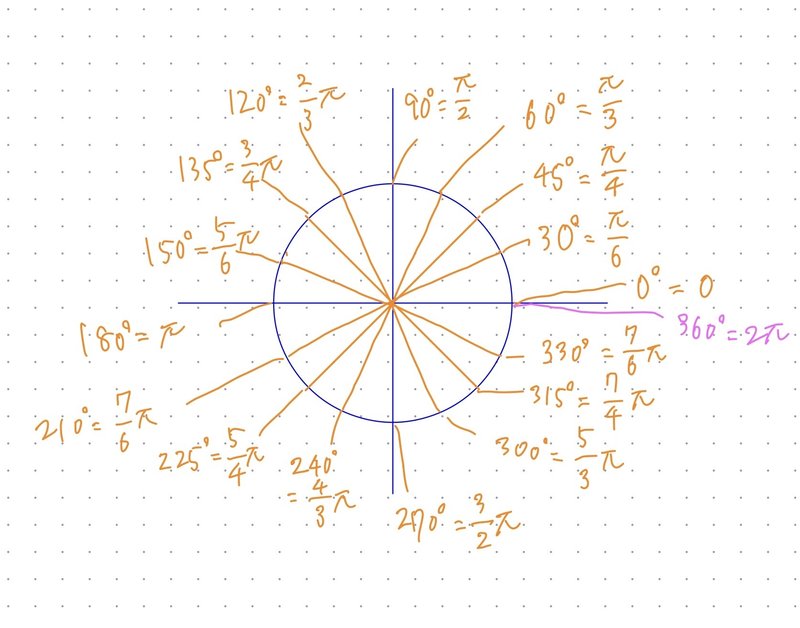
以降、単位のラジアンは省略して使用します。
また、$${0}$$を下回る角や、$${2\pi}$$を超える角も考えることとします。

ii. 三角関数のグラフ

三角関数のグラフは以下の通りです。

$${y=\sin x}$$のグラフ

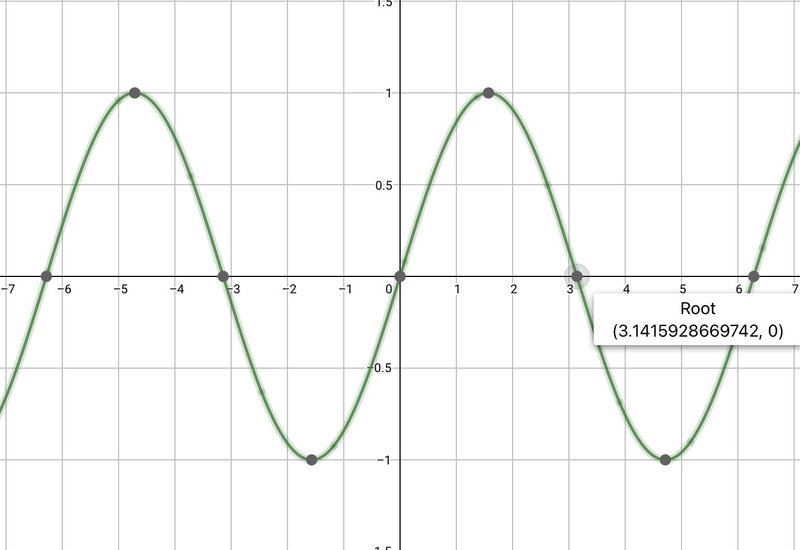
周期は$${2\pi}$$で、値域は$${-1 \le \sin x \le 1 }$$です。

$${y=\cos x}$$のグラフ

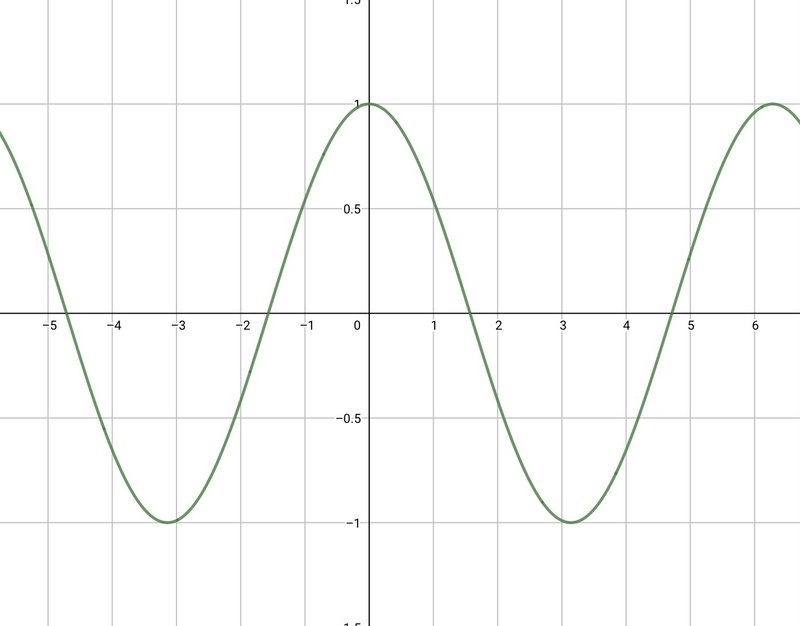
周期は$${2\pi}$$で、値域は$${-1 \le \cos x \le 1 }$$です。

$${y=\tan x}$$のグラフ

定義域は$${\frac{n}{2}\pi}$$を除いた部分、値域は実数全体です。

iii. 三角関数の角変換

三角関数の角の変換公式をいくつか紹介いたします。

●$${\frac{\pi}{2}- \theta \to \theta }$$

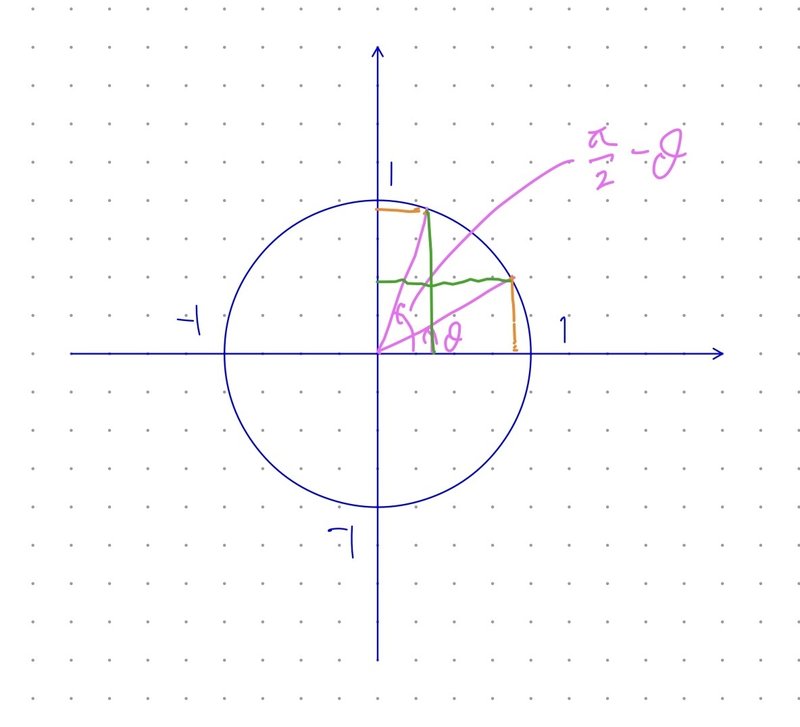
$$
\sin (\frac{\pi}{2}- \theta) = \cos \theta
$$

$$
\cos (\frac{\pi}{2}- \theta) = \sin \theta
$$

$$
\tan (\frac{\pi}{2}- \theta) = \frac{1}{\tan \theta}
$$

●$${\pi- \theta \to \theta }$$

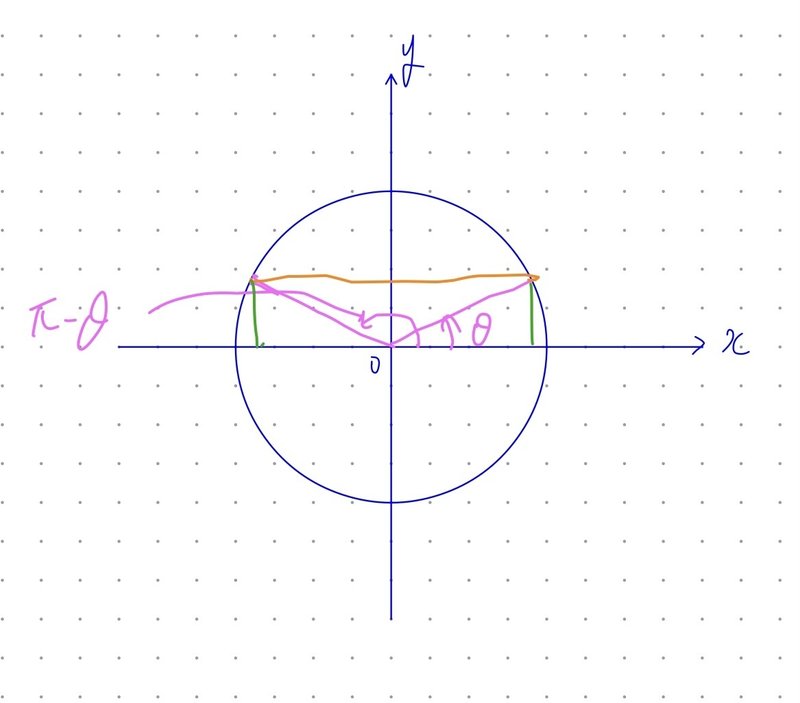
$$
\sin(\pi-\theta)=\sin \theta
$$

$$
\cos(\pi-\theta)=-\cos \theta
$$

$$
\tan(\pi-\theta)=-\tan \theta
$$

●$${- \theta \to \theta }$$

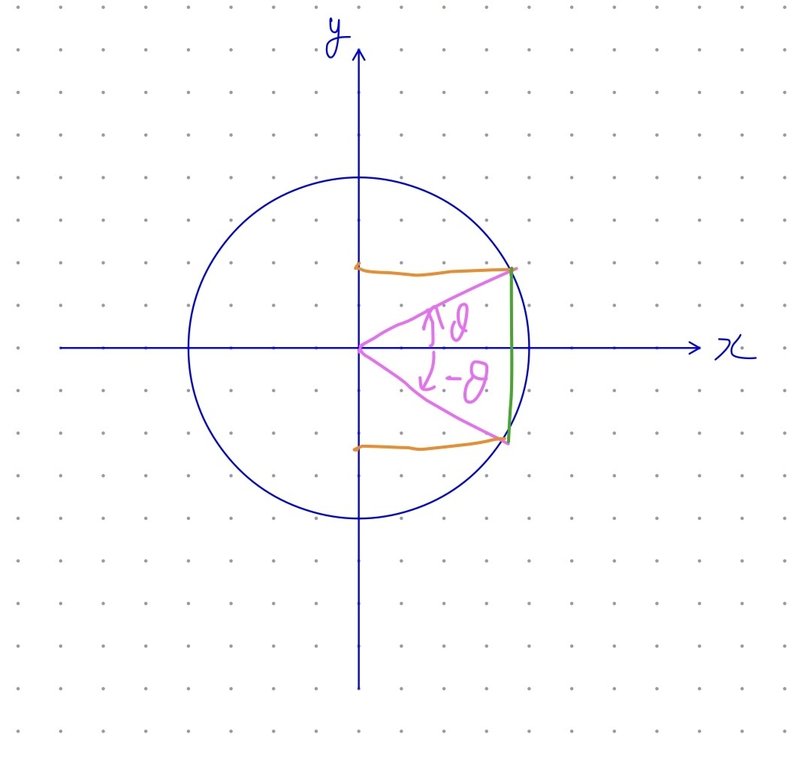
$$
\sin(-\theta)=-\sin \theta
$$

$$
\cos(-\theta)=\cos \theta
$$

$$
\tan(-\theta)=-\tan \theta
$$

●$${\theta+\frac{\pi}{2} \to \theta }$$

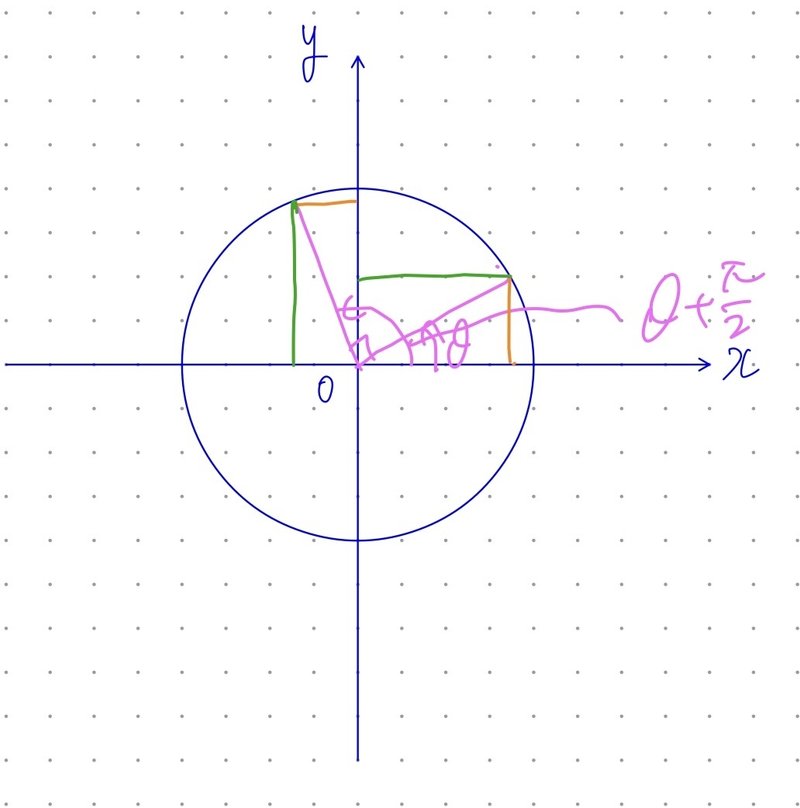
$$
\sin (\theta+\frac{\pi}{2})=\cos\theta
$$

$$
\cos (\theta+\frac{\pi}{2})=-\sin\theta
$$

$$
\tan (\theta+\frac{\pi}{2})=-\frac{1}{\tan\theta}
$$

これらは、単位円からすぐに導くことができるので、丸暗記はしない方が良いです。

iv. 三角関数の加法定理

三角関数には加法定理が存在します。

$$
\sin(\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \cdots(1)
$$

$$
\sin(\alpha-\beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \cdots(2)
$$

$$
\cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \cdots(3)
$$

$$
\cos(\alpha-\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \cdots(4)
$$

$$
\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \cdots(5)
$$

$$
\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \cdots(6)
$$

以降で、この定理を証明しますが、大学受験生はこの公式を丸暗記しましょう。

【証】

（1）

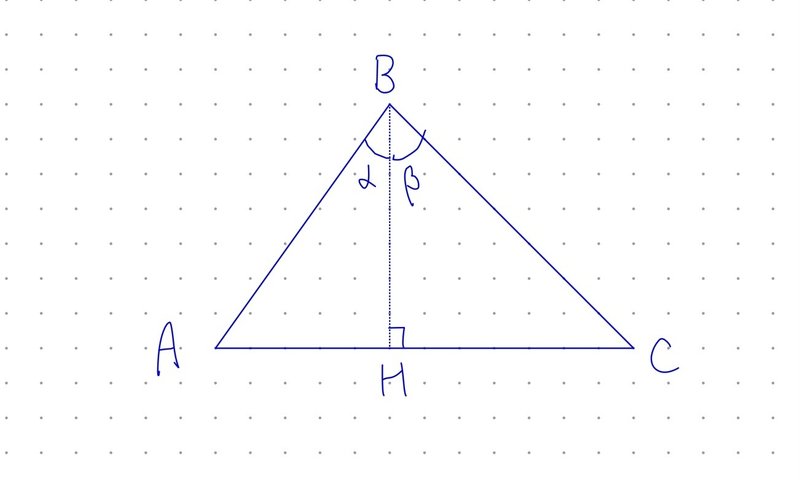
上図のように$${\triangle ABC}$$を描き、$${B}$$から$${AC}$$に下ろした垂線の足を$${H}$$とする。$${\angle ABH = \alpha, \angle CBH = \beta}$$とする。

$${\triangle ABC, \triangle ABH, \triangle CBH}$$の面積をそれぞれ$${S, S_{1}, S_{2}}$$とすると、

$$
S=\frac{1}{2}BABC\sin(\alpha+\beta)
$$

$$
S_{1}=\frac{1}{2}BABH \sin \alpha
$$

$$
S_{2}=\frac{1}{2}BCBH \sin \beta
$$

ここで、$${BH}$$を$${\beta}$$を用いて表すと、$${BH=BC\cos\beta}$$
また、$${\alpha}$$を用いて表すと、$${BH=BA\cos \alpha}$$

これより、

$$
S_{1}=\frac{1}{2}BABC\cos \beta \sin \alpha=\frac{1}{2}BABC\sin \alpha\cos \beta
$$

$$
S_{2}=\frac{1}{2}BCBA\cos \alpha \sin \beta = \frac{1}{2}BABC\cos \alpha \sin \beta
$$

$${S=S_{1}+S_{2}}$$であるから、

$$
\frac{1}{2}BABC\sin(\alpha+\beta)=\frac{1}{2}BABC\sin \alpha\cos \beta+\frac{1}{2}BABC\cos \alpha \sin \beta
$$

$$
\therefore \sin(\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta
$$

(2)

(1)で$${\beta}$$を$${-\beta}$$に置き換えると、

$$
\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\cos\alpha\sin(-\beta)
$$

$$
= \sin \alpha \cos \beta - \cos \alpha \sin \beta
$$

先に(4)を示します。

(4)

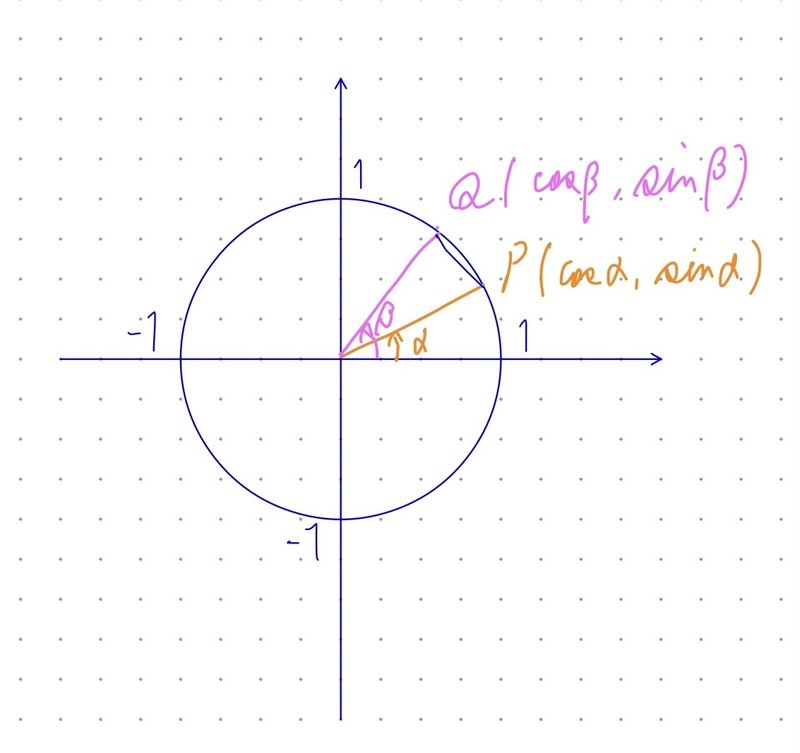
上図のように取ると、余弦定理より

$$
PQ^2=OP^2+OQ^2-2OPOQ\cos(\beta-\alpha)
$$

$$
=1+1-2\cdot1\cdot1\cdot\cos(-(\beta-\alpha))=2-2\cos(\alpha-\beta) \cdots(*)
$$

また、$${PQ}$$2点間の距離を求めると、

$$
PQ^2 = (\cos\beta-\cos\alpha)^2+(\sin\beta-\sin\alpha)^2
$$

$$
=\cos^2\beta-2\cos\beta\cos\alpha+\cos^2\alpha+\sin^2\beta-2\sin\beta\sin\alpha+\sin^2\alpha
$$

$$
=(\cos^2\beta+\sin^2\beta)+(\cos^2\alpha+\sin^2\alpha)-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)
$$

$$
=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)
$$

これと$${(*)}$$より、

$$
2-2\cos(\alpha-\beta)=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)
$$

$$
\therefore \cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta
$$

(4)

(3)で$${\beta}$$を$${-\beta}$$に置き換えると、

$$
\cos(\alpha+\beta)=\cos(\alpha-(-\beta)) = \cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)
$$

$$
=\cos\alpha\cos\beta-\sin\alpha\sin\beta
$$

(5)

$${\frac{(1)}{(3)}}$$をやると、

$$
\tan(\alpha+\beta)=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta}
$$

$$
=\frac{\frac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}+\frac{ \cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{1-\frac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}
$$

$$
=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}
$$

(6)

$${\frac{(2)}{(4)}}$$をやると、

$$
\tan(\alpha-\beta)=\frac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)}=\frac{\sin \alpha \cos \beta - \cos \alpha \sin \beta}{\cos \alpha \cos \beta + \sin \alpha \sin \beta}
$$

$$
=\frac{\frac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta} - \frac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{1 + \frac{\sin \alpha\sin \beta}{\cos \alpha \cos \beta}}
$$

$$
=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}
$$

【証明終】

練習問題

加法定理を用いて、以下の値を求めよ
(1)$${\sin 15^\circ}$$
(2)$${\sin 75^\circ}$$
(3)$${\cos 15^\circ}$$
(4)$${\cos 75^\circ}$$

v. 2倍角の公式

sin

$$
\sin 2\theta = 2\sin\theta\cos\theta
$$

$${\because}$$加法定理(1)で、$${\alpha=\beta=\theta}$$とすると、

$$
\sin(\theta+\theta)=\sin\theta\cos\theta+\cos\theta\sin\theta
$$

$$
\therefore \sin 2\theta = 2\sin\theta\cos\theta
$$

cos

$$
\cos 2\theta = \cos^2 \theta-\sin^2 \theta
$$

$$
=2\cos^2\theta-1 \cdots(i)
$$

$$
=1-2\sin^2 \theta \cdots(ii)
$$

$${\because}$$加法定理(3)で、$${\alpha=\beta=\theta}$$とすると、

$$
\cos(\theta+\theta)=\cos\theta\cos\theta+\sin\theta\sin\theta
$$

$$
\cos 2\theta = \cos^2 \theta-\sin^2 \theta
$$

$${\sin^2\theta=1-\cos^2\theta}$$であるから、

$$
\cos 2\theta = \cos^2 \theta-(1-\cos^2\theta)= 2\cos^2\theta-1
$$

また、$${\cos^2\theta=1-\sin^2\theta}$$であるから、

$$
\cos 2\theta = 1-\sin^2\theta-\sin^2 \theta=1-2\sin^2 \theta
$$

tan

$$
\tan2\theta=\frac{2\tan\theta}{1-\tan^2\theta}
$$

$${\because}$$加法定理(5)で、$${\alpha=\beta=\theta}$$とすると、

$$
\tan(\theta+\theta)=\frac{\tan\theta+\tan\theta}{1-\tan\theta\tan\theta} 
$$

$$
\therefore \tan2\theta=\frac{2\tan\theta}{1-\tan^2\theta}
$$

vi. 半角公式

sin

$$
\sin^2\frac{\theta}{2}=\frac{1-\cos\theta}{2}
$$

$${\because (ii)}$$を変形すると、

$$
2\sin^2 \theta=1-\cos2\theta
$$

$$
\sin^2 \theta = \frac{1-\cos2\theta}{2}
$$

$$
\therefore \sin^2\frac{\theta}{2}=\frac{1-\cos\theta}{2}
$$

cos

$$
\cos^2\frac{\theta}{2}=\frac{1+\cos\theta}{2}
$$

$${\because (i)}$$を変形すると、

$$
2\cos^2\theta=\cos2\theta+1
$$

$$
\cos^2\theta=\frac{\cos2\theta+1}{2}
$$

$$
\therefore \cos^2\frac{\theta}{2}=\frac{1+\cos\theta}{2}
$$

v. 三角関数の合成

sinで合成

$$
a\sin\theta+b\cos\theta = \sqrt {a^2+b^2}\sin(\theta+\alpha)
$$

ただし、$${\alpha}$$は、$${\cos\alpha=\frac{a}{\sqrt {a^2+b^2}}, \sin\alpha=\frac{b}{\sqrt {a^2+b^2}}}$$を満たす角。

【証】

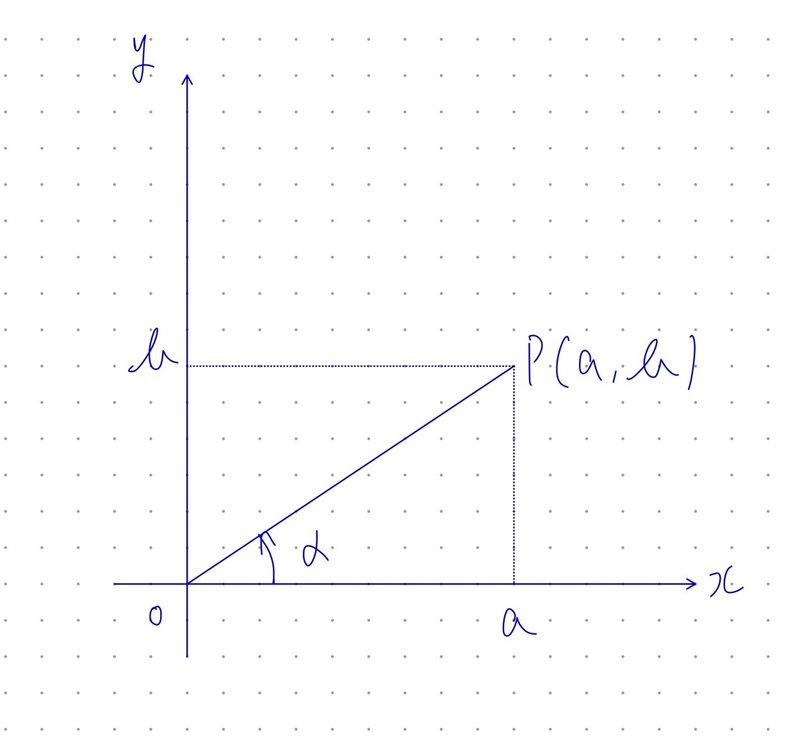
上図のように$${a, b}$$をとり、$${x}$$軸と、直線$${OP}$$とのなす角を$${\alpha}$$とする。

$$
a=\sqrt{a^2+b^2}\cos\alpha, b=\sqrt{a^2+b^2}\sin\alpha
$$

とおき、これを$${a\sin\theta+b\cos\theta}$$に代入すると、

$$
a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\cos\alpha\sin\theta+\sqrt{a^2+b^2}\sin\alpha\cos\theta
$$

$$
=\sqrt{a^2+b^2}(\sin\theta\cos\alpha+\cos\theta\sin\alpha)=\sqrt {a^2+b^2}\sin(\theta+\alpha)
$$

（$${\because}$$加法定理(1)）

$$
\cos\alpha=\frac{a}{\sqrt {a^2+b^2}}, \sin\alpha=\frac{b}{\sqrt {a^2+b^2}}
$$

【証明終】

cosで合成

2021年度の大学入試共通テストで出題されたのでcosでの合成についてもまとめます。

$$
a\cos\theta+b\sin\theta = \sqrt {a^2+b^2}\cos(\theta-\alpha)
$$

ただし、$${\alpha}$$は、$${\cos\alpha=\frac{a}{\sqrt {a^2+b^2}}, \sin\alpha=\frac{b}{\sqrt {a^2+b^2}}}$$を満たす角。

【証】

sinで合成する場合のように図をとり、

$$
a=\sqrt{a^2+b^2}\cos\alpha, b=\sqrt{a^2+b^2}\sin\alpha
$$

とおき、これを$${a\cos\theta+b\sin\theta}$$に代入すると、

$$
a\cos\theta+b\sin\theta=\sqrt{a^2+b^2}\cos\alpha\cos\theta+\sqrt{a^2+b^2}\sin\alpha\sin\theta
$$

$$
=\sqrt{a^2+b^2}(\cos\theta\cos\alpha+\sin\theta\sin\alpha)=\sqrt{a^2+b^2}\cos(\theta-\alpha)
$$

（$${\because}$$加法定理(4)）

$$
\cos\alpha=\frac{a}{\sqrt {a^2+b^2}}, \sin\alpha=\frac{b}{\sqrt {a^2+b^2}}
$$

【証明終】

練習問題

次の式を括弧内の関数で合成せよ。

(1)$${\sin\theta+\cos\theta}$$ $${(\sin)}$$
(2)$${\sin\theta+\sqrt{3}\cos\theta}$$ $${(\sin)}$$
(3)$${2\sin\theta+2\cos\theta}$$ $${(\cos)}$$
(4)$${2\sqrt{3}\sin\theta+2\cos\theta}$$ $${(\cos)}$$

vi. 積和の公式

$$
\sin\alpha\cos\beta=\frac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\} \cdots(I)
$$

$$
\cos\alpha\sin\beta=\frac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\}\cdots(II)
$$

$$
\cos\alpha\cos\beta=\frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}\cdots(III)
$$

$$
\sin\alpha\sin\beta=-\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}\cdots(IV)
$$

【証】

(I)加法定理(1)+(2)をすると、

$$
\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta
$$

$$
\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta
$$

$${+)}$$

$$
\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta
$$

$$
\therefore\sin\alpha\cos\beta=\frac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}
$$

(II)加法定理(1)-(2)をすると、

$$
\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta
$$

$$
\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta
$$

$${-)}$$

$$
\sin(\alpha+\beta)-\sin(\alpha-\beta)=2\cos\alpha\sin\beta
$$

$$
\therefore\cos\alpha\sin\beta=\frac{1}{2}\sin(\alpha+\beta)-\sin(\alpha-\beta)
$$

(III)加法定理(3)+(4)をすると、

$$
\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
$$

$$
\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta
$$

$${+)}$$

$$
\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta
$$

$$
\therefore\cos\alpha\cos\beta=\frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}
$$

(IV)加法定理(3)-(4)をすると、

$$
\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
$$

$$
\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta
$$

$${-)}$$

$$
\cos(\alpha+\beta)-\cos(\alpha-\beta)=-2\sin\alpha\sin\beta
$$

$$
\therefore\sin\alpha\sin\beta=-\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}
$$

【証明終】

vii. 和積の公式

$$
\sin A+\sin B=2\sin \frac{A+B}{2}\cos\frac{A-B}{2}
$$

$$
\sin A-\sin B=2\cos \frac{A+B}{2}\sin\frac{A-B}{2}
$$

$$
\cos A+\cos B=2\cos \frac{A+B}{2}\cos\frac{A-B}{2}
$$

$$
\cos A-\cos B=-2\sin \frac{A+B}{2}\sin\frac{A-B}{2}
$$

【証】

$${\alpha+\beta=A,\alpha-\beta=B}$$とおくと、
$${\alpha=\frac{A+B}{2}, \beta=\frac{A-B}{2}}$$

積和の公式$${(I)}$$〜$${(IV)}$$に代入して、

(I)

$$
\sin\frac{A+B}{2}\cos\frac{A-B}{2}=\frac{1}{2}(\sin A+\sin B)
$$

$$
\therefore \sin A+\sin B=2\sin \frac{A+B}{2}\cos\frac{A-B}{2}
$$

(II)

$$
\cos\frac{A+B}{2}\sin\frac{A-B}{2}=\frac{1}{2}(\sin A-\sin B)
$$

$$
\therefore \sin A-\sin B=2\cos \frac{A+B}{2}\sin\frac{A-B}{2}
$$

(III)

$$
\cos\frac{A+B}{2}\cos\frac{A-B}{2}=\frac{1}{2}(\cos A+\cos B)
$$

$$
\therefore \cos A+\cos B=2\cos \frac{A+B}{2}\cos\frac{A-B}{2}
$$

(IV)

$$
\sin\frac{A+B}{2}\sin\frac{A-B}{2}=-\frac{1}{2}(\cos A-\cos B)
$$

$$
\therefore \cos A-\cos B=-2\sin \frac{A+B}{2}\sin\frac{A-B}{2}
$$

【証明終】

viii. 三角関数の極限

$$
\lim_{\theta \to 0}\frac{\sin\theta}{\theta} = 1
$$

感覚的な説明

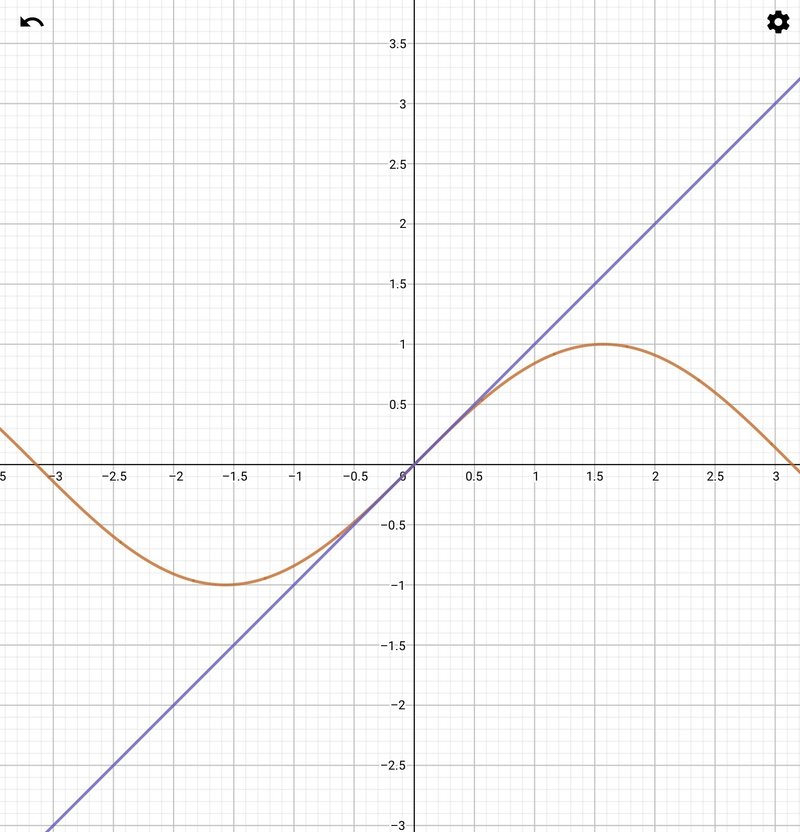
$${y=\sin x}$$のグラフと$${y=x}$$のグラフを重ねると、$${x=0}$$付近では、どちらも傾きが1であるように見えるから。

【証】（扇型の面積が$${\pi r^2\frac{\theta}{2\pi}=\frac{r^2\theta}{2}}$$で求められることがわかっている前提での証明になり、正確な証明ではありません）

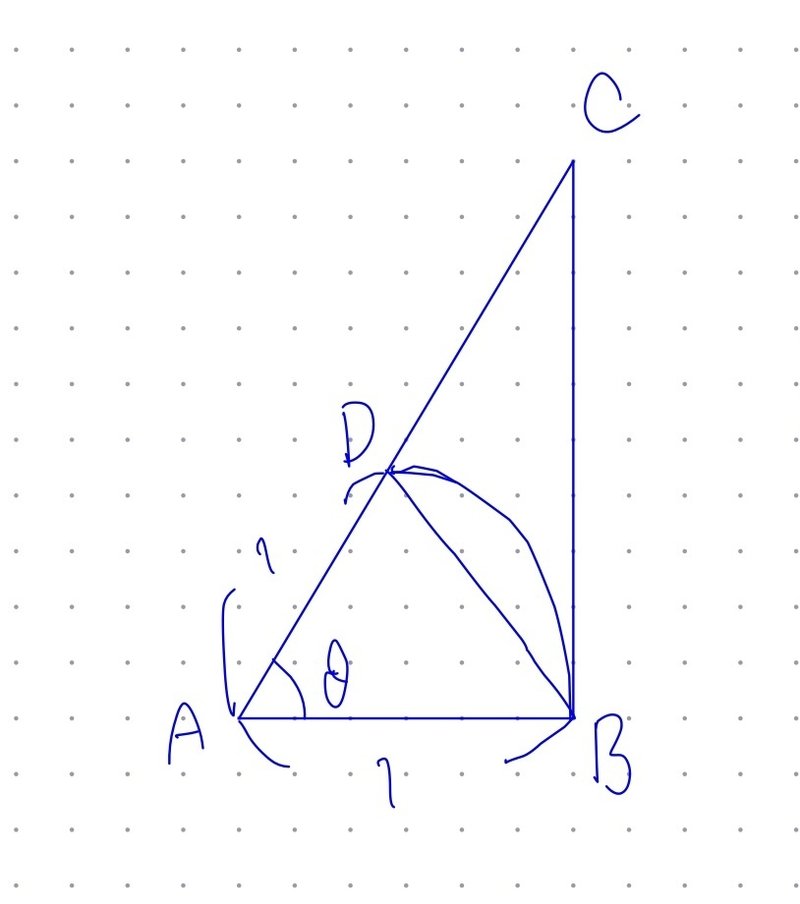
上図のようにとり、
$${\triangle ABC}$$, 扇型$${ABD}$$, $${\triangle ABD}$$の面積をそれぞれ、$${S, S_{1},S_{2}}$$とおくと、

$$
S_{2} < S_{1} < S
$$

が成り立つ。

$$
S_{2}=\frac{1}{2}\sin\theta
$$

$$
S_{1}=\frac{\theta}{2}
$$

$$
S=\frac{1}{2}\tan\theta
$$

であるから、

$$
\frac{1}{2}\sin\theta < \frac{\theta}{2} < \frac{1}{2}\tan\theta = \frac{1}{2}\frac{\sin\theta}{\cos\theta}
$$

$$
\sin\theta < \theta < \frac{\sin\theta}{\cos\theta}
$$

逆数を取ると、

$$
\frac{\cos\theta}{\sin\theta} < \frac{1}{\theta} < \frac{1}{\sin\theta}
$$

$$
\cos\theta < \frac{\sin\theta}{\theta} < 1
$$

$${\lim_{\theta \to 0}\cos\theta=1}$$であるから、はさみうちの原理より、

$$
\lim_{\theta \to 0}\frac{\sin\theta}{\theta} = 1
$$

【証明終】

⒊ 三角関数の微分

では、準備が整ったところで、三角関数の微分に入ります。

i. sinの微分

$$
(\sin x)'=\lim_{\Delta x \to 0}\frac{\sin(x+\Delta x)-\sin x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{\sin x\cos\Delta x+\cos x\sin \Delta x-\sin x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}(\frac{\sin x(\cos\Delta x-1)}{\Delta x}+\frac{\cos x\sin \Delta x}{\Delta x})
$$

$$
=\lim_{\Delta x \to 0}(\frac{\sin x(\cos^2\Delta x-1)}{\Delta x(\cos\Delta x+1)}+\cos x\frac{\sin \Delta x}{\Delta x})
$$

$$
=\lim_{\Delta x \to 0}(\frac{\sin x(-\sin^2\Delta x)\Delta x}{\Delta x^2(\cos\Delta x+1)}+\cos x\frac{\sin \Delta x}{\Delta x})
$$

$$
=\lim_{\Delta x \to 0}(-\sin x\frac{\sin^2\Delta x}{\Delta x^2}\frac{\Delta x}{(\cos\Delta x+1)}+\cos x\frac{\sin \Delta x}{\Delta x})
$$

$$
=\cos x
$$

$$
\because \lim_{\Delta x \to 0}\frac{\Delta x}{(\cos\Delta x+1)}=\frac{0}{2}=0
$$

$$
\lim_{\Delta x \to 0}\frac{\sin \Delta x}{\Delta x}=1
$$

したがって、

$$
(\sin x)'=\cos x
$$

となります。

ii. cosの微分

$$
(\cos x)'=\lim_{\Delta x \to 0}\frac{\cos(x+\Delta x)-\cos x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{\cos x\cos\Delta x-\sin x \sin\Delta x-\cos x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}(\frac{\cos x(\cos\Delta x-1)}{\Delta x}-\sin x\frac{ \sin\Delta x}{\Delta x})
$$

$$
=\lim_{\Delta x \to 0}(\frac{\cos x(\cos^2\Delta x-1)}{\Delta x(\cos\Delta x+1)}-\sin x\frac{\sin \Delta x}{\Delta x})
$$

$$
=\lim_{\Delta x \to 0}(\frac{\cos x(-\sin^2\Delta x)\Delta x}{\Delta x^2(\cos\Delta x+1)}-\sin x\frac{\sin \Delta x}{\Delta x})
$$

$$
=\lim_{\Delta x \to 0}(-\cos x\frac{\sin^2\Delta x}{\Delta x^2}\frac{\Delta x}{(\cos\Delta x+1)}-\sin x\frac{\sin \Delta x}{\Delta x})
$$

$$
=-\sin x
$$

$$
\because \lim_{\Delta x \to 0}\frac{\Delta x}{(\cos\Delta x+1)}=\frac{0}{2}=0
$$

$$
\lim_{\Delta x \to 0}\frac{\sin \Delta x}{\Delta x}=1
$$

したがって、

$$
(\cos x)'=-\sin x
$$

となります。

iii. tanの微分

$$
(\tan x)'=\lim_{\Delta x \to 0}\frac{\tan(x+\Delta x)-\tan x}{\Delta x}
$$

$$
=\lim_{\Delta x \to 0}\frac{1}{\Delta x}(\frac{\tan x +\tan \Delta x}{1-\tan x \tan \Delta x}-\tan x)
$$

$$
=\lim_{\Delta x \to 0}\frac{1}{\Delta x}(\frac{\tan x +\tan \Delta x-\tan x+\tan^2 x\tan\Delta x}{1-\tan x \tan \Delta x})
$$

$$
=\lim_{\Delta x \to 0}\frac{1}{\Delta x}\{\frac{\tan \Delta x(1+\tan^2 x)}{1-\tan x \tan \Delta x}\}
$$

$$
=\lim_{\Delta x \to 0}\frac{1}{1-\tan x \tan \Delta x}\frac{\sin \Delta x}{\Delta x}\frac{1}{\cos \Delta x}\frac{1}{\cos^2 x}
$$

$$
= \frac{1}{\cos^2 x}
$$

$$
\because\lim_{\Delta x \to 0}\frac{1}{1-\tan x \tan \Delta x}=\frac{1}{1-0}=1
$$

$$
\lim_{\Delta x \to 0}\frac{\sin \Delta x}{\Delta x}=1
$$

$$
\lim_{\Delta x \to 0}\frac{1}{\cos \Delta x}=\frac{1}{1}=1
$$

$$
1+\tan^2 x=\frac{1}{\cos^2x}
$$

したがって、

$$
(\tan x)' = \frac{1}{\cos^2x}
$$

⒋ 三角関数の積分

積分は、微分の逆を行えば良いので、

cosの積分

$${(\sin x)'=\cos x}$$より、

$$
\int \cos x dx = \sin x +C
$$

sinの積分

$${(\cos x)'=-\sin x}$$より、

$$
\int \sin x dx = -\cos x +C
$$

1/cos^2xの積分

$${(\tan x)' = \frac{1}{\cos^2x}}$$より、

$$
\int \frac{1}{\cos^2x} dx = \tan x + C
$$

※$${\int\tan x dx}$$については、別のnoteで紹介します。
また、$${\sin 2x}$$など、角の部分を定数倍したものの微分積分についても、別のnoteで紹介します。

まとめ

今回のnoteは、三角比および三角関数の概要を知った上で、三角関数の微分積分を説明したかったので、かなり長くなってしまいました。

三角関数（正確にはフーリエ解析）は心電図や音波の可視化などによく使われるので、理系に進まれる方は、しっかりと押さえておく必要があります。

フーリエ解析については理系の大学で学ぶので、それまでに三角関数とそれらの微分積分についてしっかりと学習しておくことをお勧めします。

#数学がすき #数学 #三角比 #三角関数 #sin #cos # tan #正弦定理 #余弦定理 #加法定理 #極限 #微分 #積分 #mathematics #trigonometric #ratio #function #limit #calculus #differentiation #integration