消費者の好みを反映した効用関数をベースに、予算の制約下で消費者が採る最適な消費行動がどのような性質を持つかを議論する。連載はこちら。

予算制約式と効用最大化問題

効用関数の導入により、消費者の合理的行動(選択肢$${S}$$内の任意の$${x}$$に対して$${x^*≻x}$$となるような$${x^*}$$を選択する行動)は効用最大化問題の解として解析的に取り扱うことが可能となる。但し、現実的には無限に財を購入し消費することは不可能であるため、有限の予算制約の中で効用を最大にする$${x^*}$$を求める必要がある。

従って、合理的に行動する消費者の消費行動は、予算制約式$${p\cdot x=I}$$を満たす消費計画$${x}$$の中で、効用$${u(x)}$$を最大にするもの(最適消費計画)を選ぶ問題として定式化される。

なお、消費者や企業は所与の価格体系をコントロールできないものと仮定しており、これをプライス・テイカーの仮定という。従って消費者にとって価格$${p}$$は外生的に受け入れざるを得ないが、消費ベクトル$${x}$$は選択できるため、予算制約$${p\cdot x=I}$$も設定可能である。

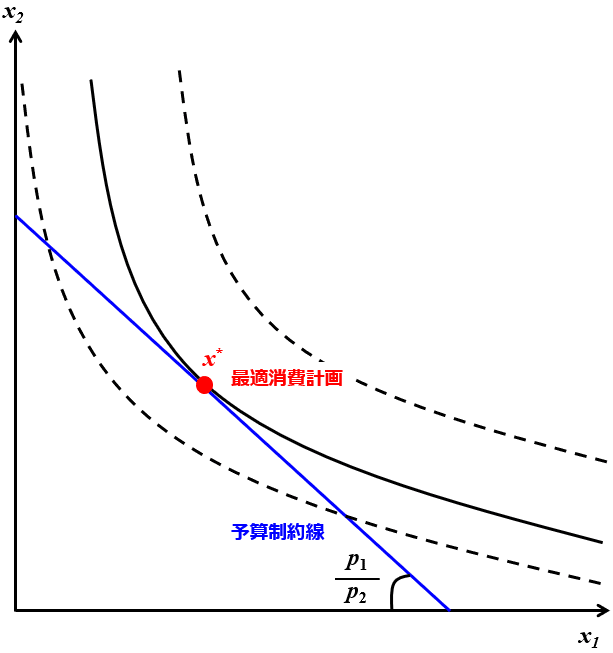
例として、$${x_1, x_2}$$の2財からなる経済を考える。この最適消費計画問題において、予算制約式を満たす様々な消費計画は、予算制約式：$${p_1x_1+p_2x_2=I ⇔ x_2=-\dfrac{p_1}{p_2}x_1+\dfrac{I}{p_2}}$$で表す直線(予算線)で示される。予算線の傾きは、価格の比率$${\dfrac{p_1}{p_2}}$$である。予算線の下側を消費可能集合と呼ぶが、無差別曲線が予算線と交わる場合(以下図で予算線と、左下の点線で表された無差別曲線の位置関係)、その無差別曲線の上方位集合の中に消費可能集合が存在することになり、その無差別曲線上の消費計画はいずれも最適消費の条件を満たさない。逆に無差別曲線が予算線と交わらない場合(予算線と右上の点線で表された無差別曲線の位置関係)、その無差別曲線上のいずれの消費計画も消費可能集合に含まれないためこの最適消費計画問題の解とならない。従って、最適消費計画$${x^*}$$は、予算線と無差別曲線の接点として求まる。

限界効用と限界代替率

経済学における「限界」概念

これまで効用関数や無差別曲線の形状について議論してきたのは、財の消費量の変化によって消費者の好みがどのように変化するかを記述するためであった。例えば非飽和性の議論では「うどんが1杯、2杯、…」と離散的な量の変化に対する効用の変化を例示したが、ここからは財が必要な分だけ十分小さい単位に分割可能なものと仮定する。経済学における「限界」とは、変数(財の消費量などの)を連続的に微少量だけ(=限界的に)変化させた時の目的関数(効用など)の変化量を表す概念であり、数学の微分と同じ概念である。図の上では目的関数上のある点に接する曲線の傾きとして表現される。

限界効用

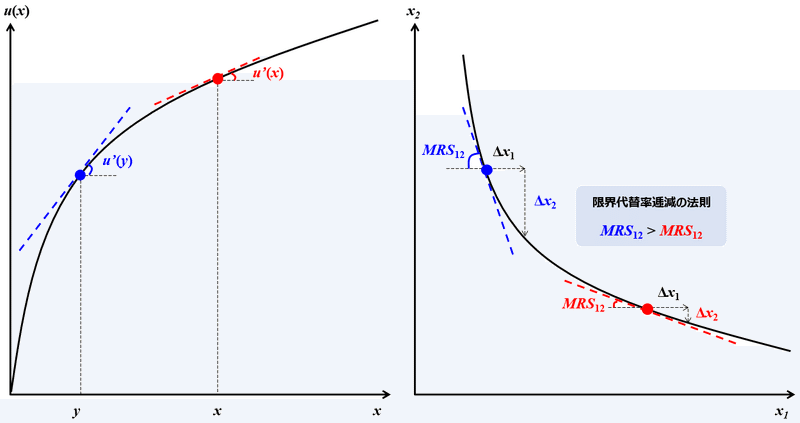
限界効用とは、他の財の消費量を固定し、第$${i}$$財の消費量$${x_i}$$が微少量変化した時の効用の変化量を表す。効用関数を$${x_i}$$のみの関数として$${u}$$を$${x_i}$$で微分することで定義される(Marginal Utilityの頭文字を取り$${MU_i}$$と表記)。図形的には、限界効用は効用関数の$${x_i}$$上における接線の傾きで表される(2財モデルにおける図形的イメージは以下の左図)。

効用関数が凹性を満たす時、$${x_i}$$の増加に伴い$${MU_i}$$は減少する。これを限界効用の逓減という。例えば、毎日うどんを食べる生活を続けていると、如何にうどんが好物かつ空腹と言えど、代り映えのしない食生活に飽きて満足度が下がり別のものを食べたいと思うようになる場合や、スマホゲームのガチャで同じアイテムが当たり続け、追加的に1つ当たった時の満足度の上昇幅は、そのアイテムの所有量が多くなるにつれ薄まっていく、という状況に該当する。数学的には効用関数$${u}$$が凹関数$${⇔}$$効用関数の2階導関数が負$${(u''<0)}$$であることに対応する(証明にはLagrangeの平均値の定理を用いる)。なお、選好関係$${≿}$$の標準的な公理系における凸性の仮定の下では効用関数は準凹性は満たすが凹性は必ずしも満たさないため、限界効用は必ずしも逓減しない。

限界代替率

限界代替率とは、特定の2財における主観的な交換比率を表す。例えば$${x_1}$$の消費を微少量減らした$${(\Delta x_1 < 0)}$$際に、元の効用を維持するための$${x_2}$$の消費量の増分$${\Delta x_2 >0}$$の比率$${-\dfrac{\Delta x_2}{\Delta x_1}}$$(正値にするため負号を付している)の極限であり、$${x_2}$$を$${x_1}$$で微分することで定義される。これを第1財の第2財に対する限界代替率と言い、Marginal Rate of Substitutionの頭文字を取り$${MRS_{12}}$$と表す。従ってここで示されているのは、第2財で計った第1財の価値である。図形的には、限界代替率は無差別曲線上における接線の傾きで表される(2財モデルにおける図形的イメージは以下の右図)。

ここで、2財モデルの効用関数$${u=u(x_1, x_2)}$$の全微分は$${\mathrm{d}u=\dfrac{\partial u}{\partial x_1}\mathrm{d}x_1+\dfrac{\partial u}{\partial x_2}\mathrm{d}x_2}$$と表されるが、無差別曲線の条件：$${\mathrm{d}u =0}$$を代入し整理することで、以下の限界効用と限界代替率の関係、すなわち限界代替率は限界効用の比であることが分かる。

限界代替率逓減の法則
標準的な公理系における選好関係$${≿}$$は凸性を仮定しているため、無差別曲線は原点に対して凸となる。無差別曲線$${I(x)}$$が凸関数$${⇔}$$無差別曲線の2階導関数が正$${(I^{\prime}(x)>0)}$$であることから、無差別曲線の接線の傾きである(第1財の第2財に対する)限界代替率は、第1財の消費量増加に伴い減少する。これを限界代替率逓減の法則という。例えば、第1財：水、第2財：パンの交換を考える。ある消費者がパンを大量に(例えば500枚)保有するが水が不足しのどが渇いている時、いくらでもパンを交換に差し出し(例えば100枚)、飲み水(例えば$${1l}$$)を確保しようとするだろう。やがて交換が進み十分量の水を確保できた場合、更なる水$${1l}$$を手に入れるために差し出すパンの量は少なくなるだろう(例えば10枚)。これは差し出すパンの量が水の価値を表しており、水$${1l}$$の希少性が薄まるにつれその価値がパン100枚分→10枚分に下落した訳である。選好の凸性は通常仮定されるため、その前提において限界代替率逓減の法則も成り立つ。

補足：全微分
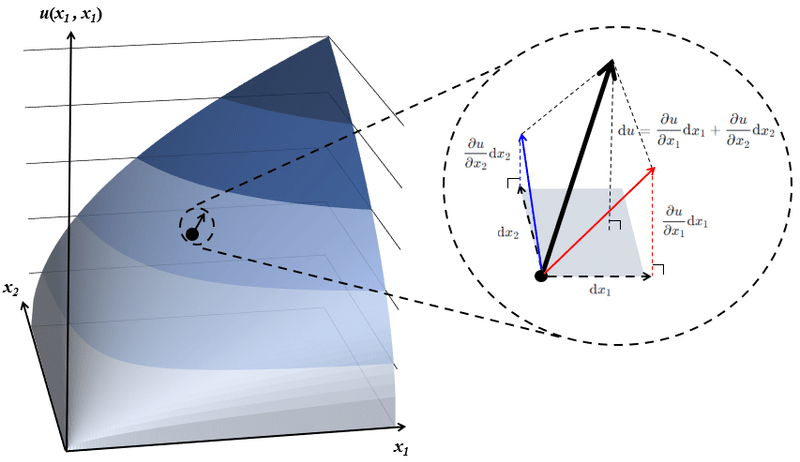
効用関数の傾きは場所により異なるため、効用関数上の点の移動の軌跡は一般に曲線を描くが、限界的な効用の変化$${\mathrm{d}u}$$をほぼ平面の一次式と見なすことで、効用の変化$${\mathrm{d}u}$$を近似的に個別効果の和として表現できる。この式を全微分と言い、微分がモデル分析で有用なのは、複雑な関数を部分的に拡大し一次式として近似的に取り扱えるためである。

最適消費の条件

ここまでの議論から、2財モデルにおいて①最適消費計画$${x^*}$$は、予算線と無差別曲線の接点である、②予算線の傾きは2財の価格の比率$${\dfrac{p_1}{p_2}}$$である、③無差別曲線の接線の傾きは限界代替率であり、④それは2財の限界効用の比である、ことが分かった。従って最適消費計画$${x^*}$$が満たすべき条件を、以下の通り導ける。

最右辺の$${\dfrac{\partial u(x^*)}{\partial x_1}\dfrac{1}{p_1}}$$は、第1財に対する限界効用と1円で購入可能な第1財の量の積であり、近似的に第1財の消費を1円分だけ変化させたときの効用の変化量に等しい。仮に$${\dfrac{\partial u(x^*)}{\partial x_1}\dfrac{1}{p_1}>\dfrac{\partial u(x^*)}{\partial x_2}\dfrac{1}{p_2}}$$とすると、同金額分だけ第1財の消費を増やし第2財の消費を減らせば、予算一定のまま効用を増加させることができる。最適消費$${x^*}$$とは支出額の微調整で効用を改善できない状態なので、上式は等式で結ばれる。これを(1円あたりの)限界効用均等の法則という。財が多数存在する場合の最適条件は、以下のように表せる。

限界効用を所得で除した所得の限界効用は全ての財について等しいためこれを$${\lambda}$$とおくと、上式は以下の連立方程式として記述できる。

$${\begin{cases} \dfrac{\partial u(x^*)}{\partial x_1} &=& \lambda p_1 \\ \\ &\cdots \\ \\ \dfrac{\partial u(x^*)}{\partial x_N} &=& \lambda p_N \end{cases}}$$

これは予算制約下での効用最大化問題で、条件付最大化問題の一種である。

この問題を一般的に解くには、次のようなLagrangeの未定乗数法を用いる。目的関数$${f}$$と制約条件$${g}$$、及び未定乗数$${\lambda}$$を用いて次のLagrangian関数$${L}$$を作る。
$${L(x)=f(x)+\lambda g(x)}$$
無差別曲線の上側が凸集合かつ内点解(消費量がゼロの財が無い)ならば、最適解は必ず以下の条件を満たすことが分かっている。

$${\begin{cases} \dfrac{\partial L}{\partial x_1} &=& 0 \\ \\ &\cdots \\ \\ \dfrac{\partial L}{\partial x_N} &=& 0 \\ \\ \dfrac{\partial L}{\partial \lambda} &=& 0 \end{cases}}$$

効用関数$${u(x_1, \cdots, x_N)}$$を、制約条件$${I-p_1x_1-\cdots-p_Nx_N=0}$$の下で最大化する問題では、Lagrangian関数$${L}$$は
$${L=u+\lambda (I-p_1x_1-\cdots-p_Nx_N=0)}$$
であり、上記の条件式は

$${\begin{cases} \dfrac{\partial L}{\partial x_1} &=& \dfrac{\partial u(x^*)}{\partial x_1}-\lambda p_1 &=& 0 \\ \\ &\cdots \\ \\ \dfrac{\partial L}{\partial x_N} &=& \dfrac{\partial u(x^*)}{\partial x_N}-\lambda p_N &=& 0 \\ \\ \dfrac{\partial L}{\partial \lambda} &=& g(x^*) &=&0 \end{cases}}$$

となり、上記の最適消費が満たす連立方程式と同じものが導出される。

補足：Lagrangeの未定乗数法
有界閉領域$${D}$$において、$${C^1}$$級(1階微分可能)の関数$${f(x_1, x_2), g(x_1, x_2)}$$がある。今、$${g(x_1, x_2)=0}$$を制約条件とするとき、$${f(x_1, x_2)}$$の最大値もしくは最小値を与える点$${(x_1^*, x_2^*)}$$は、以下のいずれかの条件を満たすが、このうち3.に該当するのがLagrangeの未定乗数法である。

1. $${D}$$の境界上で、$${g(x_1^*, x_2^*)=0}$$となる端点解

2. 曲線$${g(x_1, x_2)=0}$$上の特異点
   $${i.e　(x_1^*, x_2^*)}$$が$${\dfrac{\partial g}{\partial x_1}=\dfrac{\partial g}{\partial x_2}=0}$$を満たす点は、3.の$${\lambda g(x_1, x_2)}$$の項が微分によりゼロになるため、未定乗数法で求められない解となる

3. ある実数$${\lambda}$$が存在し、$${L(x_1, x_2, \lambda)=f(x_1, x_2)-\lambda g(x_1, x_2)}$$に対して、$${(x_1^*, x_2^*, \lambda)}$$が$${\dfrac{\partial L}{\partial x_1}=\dfrac{\partial L}{\partial x_2}=\dfrac{\partial L}{\partial \lambda}=0}$$を満たす(Lagrangeの未定乗数法)

上記の最適化問題は、端点解、特異解でなければ3.により解が求まるが、1.及び2.の成否も確かめる必要がある。3.の条件を計算すると、
$${\Bigg(\dfrac{\partial f}{\partial x_1}, \dfrac{\partial f}{\partial x_2} \Bigg)=-\lambda \Bigg(\dfrac{\partial g}{\partial x_1}, \dfrac{\partial g}{\partial x_2} \Bigg)}$$
となるが、左辺は$${f}$$の勾配$${\nabla f}$$($${f}$$が最も急に上昇する方向)を表し、これが右辺の$${-\lambda \nabla g}$$と等しいため、目的関数$${f}$$と制約式$${g}$$の勾配が真逆の方向を向いていることを意味する。

次回はこちら。