＜アーベルの証明①＞差積の添加で対称性を遇置換まで絞り込む

2022年7月11日 00:36

　竹村先生が森田君の部屋に入ると、森田君は机に向かってノートを開いている。いつもなら自信あり気な森田君。今日はなにやら表情が浮かない。
「森田君どうだった？」
「途中まではできそうなんですが・・・」
　５次方程式に解の公式が存在しないことの証明は、小学５年生の森田君にはさすがに難しそう。一度整理した方がよいと感じた竹村は、森田君に問いかけた。
「具体的な証明の前に、今までの復習をしてみようか。新しいヒントが得られるかもしれないよ」
　森田君は少し口元を引き締め、「分かりました」とホワイトボードの前に立った。

1. ３次方程式に解の公式が存在する理由（復習）

「では、今までの復習を自分なりにしてみようと思います。まずは３次方程式の解の公式がなぜ導き出せるのかです。
　集合 $${Q(\omega)}$$ は３次置換で対称性を保つ式、つまり対称式の集合です。よって$${Q(\omega)}$$ 内では、対称式である差積の２乗
　$${(X_3)^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
を、３次方程式 $${y^3+py+q=0}$$ の係数 $${p, q}$$ の加減乗除で表現できます。（$${\Rightarrow}$$ 詳しくは本シリーズ (9)）
　しかし差積の２乗の平方根
　$${\sqrt{(X_3)^2}=\sqrt{\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}}$$
は $${Q(\omega)}$$ 内では表現できません。$${p, q}$$ の加減乗除だけに制限された集合 $${Q(\omega)}$$ 内では平方根を取ることはできないからです。そこで平方根 $${\sqrt{(X_3)^2}}$$ を集合 $${Q(\omega)}$$ に添加して、加減乗除で使える式を拡大します。その拡大された式の集合 $${Q(\omega, \sqrt{(X_3)^2})}$$ 内では、$${p, q}$$ と平方根 $${\sqrt{(X_3)^2}}$$ の加減乗除によって、ラグランジュ・リゾルベントの３乗
　$${A^3=(\alpha+\omega\beta+\omega^2\gamma)^3}$$
　$${B^3=(\alpha+\omega^2\beta+\omega\gamma)^3}$$
が表現できるようになります $${\text{\bf (step1)}}$$。$${\sqrt{(X_3)^2}}$$ の添加によって平方根が使えるようになることがポイントです。

$${\text{\bf (step1)}}$$ の図説

　しかしラグランジュ・リゾルベントの３乗の３乗根
　$${\sqrt[3]{A^3}=\sqrt[3]{(\alpha+\omega\beta+\omega^2\gamma)^3}}$$
　$${\sqrt[3]{B^3}=\sqrt[3]{(\alpha+\omega^2\beta+\omega\gamma)^3}}$$
は $${Q(\omega, \sqrt{(X_3)^2})}$$ 内では表現できません。$${p, q}$$ と $${\sqrt{(X_3)^2}}$$ の加減乗除だけに制限された集合 $${Q(\omega, \sqrt{(X_3)^2})}$$ 内では３乗根を取ることはできないからです。そこで集合 $${Q(\omega, \sqrt{(X_3)^2})}$$ に新たに３乗根 $${\sqrt[3]{(A_3)^3}}$$ を添加し、加減乗除で使える式を拡大します。その拡大された式の集合 $${Q(\omega, \sqrt{(X_3)^2}, \sqrt[3]{(A_3)^3})}$$ 内では、$${p, q}$$ と $${\omega}$$ と３乗根 $${\sqrt[3]{(A_3)^3}}$$ の加減乗除でラグランジュ・リゾルベントそのもの
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
　$${B=\alpha+\omega^2\beta+\omega\gamma}$$
が表現できるようになり $${\text{\bf (step2)}}$$、あとはそれらの連立方程式を解くことで $${\alpha, \beta, \gamma}$$ が決定でき、それから解の公式が得られます。（$${\Rightarrow}$$ 証明は本シリーズ (13)）

$${\text{\bf (step2)}}$$ の図説

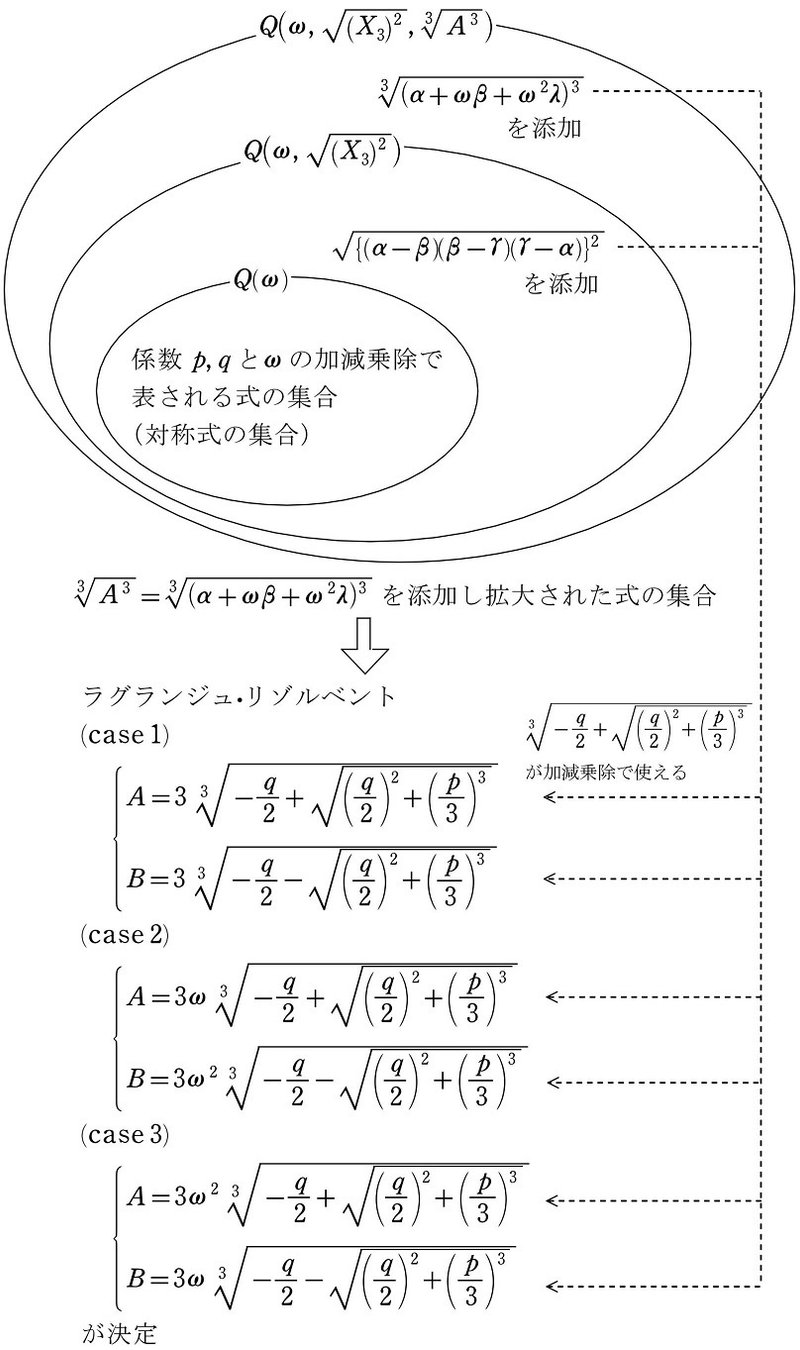
　このように平方根、３乗根と次々と添加していくことで、ラグランジュリゾルベント $${A, B}$$ を、$${p, q}$$ 及び累乗根（平方根と３乗根）を用いて表すことがでます。後はそれらの連立方程式、つまりラグランジュ・リゾルベント同士の加減乗除によって３次方程式の解の公式を導き出すことが可能となるわけです。
　なお $${\sqrt{(X_3)^2}}$$ の添加は $${X_3}$$ の添加と同じとなり、集合としても同じ範囲となります（注１）。つまり
　$${Q(\omega, \sqrt{(X_3)^2})=Q(\omega, X_3)}$$
また、$${\sqrt[3]{(A_3)^3}}$$ の添加は $${A}$$ の添加と同じとなり、集合としても同じ範囲となります（注２）。つまり
　$${Q(\omega, \sqrt{(X_3)^2}, \sqrt[3]{(A_3)^3})=Q(\omega, X_3, A)}$$
となります。

　またこれまでの過程を置換という立場で眺めれば、最初に添加した $${X_3}$$ と、それを用いて得られる $${A^3, B^3}$$ は、共に遇置換でのみ対称性を保ちます。この段階で対称性を保つ置換は、３文字すべての入れ替えである３次置換から遇置換に絞られます。対称性を「遇置換シンメトリー」まで崩すことに成功しました $${\text{\bf (step1)}}$$。
　その次に添加した $${A}$$ と、それを用いて得られる解の式 $${\alpha, \beta, \gamma}$$ は、共に恒等置換でのみ対称性を保ちます。この段階で、対称性を保つ置換は遇置換から恒等置換にまで絞られます $${\text{\bf (step2)}}$$。このように次々と都合のよい式を添加することによって、対称性を保つ置換を下図のように絞り込んでいきます。

$$
\begin{gather*}
３次置換\\
\hspace{104pt}\downarrow \Leftarrow X_3 の添加 \text{\bf (step1)}\\
遇置換\\
\hspace{100pt}\downarrow \Leftarrow A の添加 \text{\bf (step2)}\\
恒等置換
\end{gather*}
$$

いわば対称性を３次置換から恒等置換にまで崩していくことによって、最終的に恒等置換でのみ対称性を保つ解の式 $${\alpha, \beta, \gamma}$$ を作り上げることに成功、それが３次方程式の解の公式に他ならないわけです。
　なお、この対称性が崩れていく過程は、使える式の拡大に対応しています（下図）。添加によって使える式の集合が大きくなるにつれて、対称性を保つ置換が絞られていきます。

$$
\begin{gather*}
Q(\omega)\\
\hspace{67pt}\downarrow \Leftarrow X_3 の添加\\
Q(\omega, X_3)\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
Q(\omega, X_3, A)
\end{gather*}
\hspace{18pt}
\xleftrightarrow[対応]{}
\hspace{-27pt}
\begin{gather*}
３次置換\\
\hspace{67pt}\downarrow \Leftarrow X_3 の添加\\
遇置換\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
恒等置換
\end{gather*}
$$

$${X_3}$$ の添加は平方根の利用を意味していました。$${A}$$ の添加は３乗根の利用を意味していました。平方根、３乗根と使える累乗根を次々と拡大していくにつれて、逆に対称性は絞られていきます。対称性が段階的に崩れていくわけです。そして恒等置換にまで対称性を崩すことによって平方根、３乗根と必要な式が十分に備わり、最終的にそれらを用いて解の式 $${\alpha, \beta, \gamma}$$ を構成することによって解の公式が導出されたのです」
　自分が教えていない図式も取り入れ、竹村は「なるほど」とうなずいた。ここまで理解していれば証明に入れるだろう。「それでは」と竹村は立ち上がった。
「では森田君。ここで新しい表記法について勉強していこうか。何度もやってきた３文字すべての入れ替え３次置換について、新しい表記法を定義していくよ」
　竹村はホワイトボードの前に立ち、勢いで押され気味だった竹村は久しぶりに家庭教師らしい気分になった。
「では３次置換について、新しい概念と表記法を勉強しよう。

2. 巡回置換について

➀ $${\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}}$$ は、$${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ に、$${\gamma}$$ を $${\gamma}$$ に、つまりそのままで変わらない置換。カッコの中は、上の配列から下の配列に置き換えるとみるんだね。これは作用させても変化しないので『恒等置換』といい、記号 $${I}$$ と表す。

$$
\begin{align*}
\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}
=I
\end{align*}
$$

② $${\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}}$$ は、$${\alpha}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に置き換える置換。これは
　$${\alpha\rightarrow\gamma\rightarrow\beta\rightarrow\alpha}$$
と巡回する３つの文字の置換なので『３次巡回置換』といい、$${(\alpha \gamma \beta)}$$ と表す。

$$
\begin{align*}
\dbinom{\alpha \beta \gamma}{\gamma \alpha \beta}
=(\alpha \gamma \beta)
\end{align*}
$$

③　$${\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}}$$ は、 $${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ に置き換える置換。これは
　$${\alpha\rightarrow\beta\rightarrow\gamma\rightarrow\alpha}$$
と巡回する３つの文字の置換なので、これも『３次巡回置換』となり、$${(\alpha \beta \gamma)}$$ と表す。

$$
\begin{align*}
\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}
=(\alpha \beta \gamma)
\end{align*}
$$

④　$${\dbinom{\alpha \beta \gamma}{\alpha \gamma \beta}}$$ は、$${\alpha}$$ はそのままで、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換える置換。これは $${\beta}$$ と $${\gamma}$$ を入れ替える置換なので『互換』といい、$${(\beta \gamma)}$$ と表す。互換についてはすでにやったね。（$${\Rightarrow}$$ 詳しくは本シリーズ (8)）

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
$$

なお、互換は２つの文字の巡回置換『２次巡回置換』とみることもできる。

➄　$${\dbinom{\alpha \beta \gamma}{\gamma \beta \alpha}}$$ は、$${\alpha}$$ を $${\gamma}$$ に、$${\beta}$$ はそのままで、$${\gamma}$$ を $${\alpha}$$ に置き換える置換。これは $${\alpha}$$ と $${\gamma}$$ を入れ替える置換なので『互換』となり、$${(\alpha \gamma)}$$ と表す。

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}
$$

⑥　$${\dbinom{\alpha \beta \gamma}{\beta \alpha \gamma}}$$ は、$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に、$${\gamma}$$ は変化しない置換。これは $${\alpha}$$ と $${\beta}$$ 入れ替える置換なので『互換』となり、 $${(\alpha \beta)}$$ と表す。

$$
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
$$

　一般に $${n}$$ 個の文字の巡回置換を『$${\boldsymbol{n}}$$ 次巡回置換』という。
　例えば４次置換 $${\dbinom{\alpha \beta \gamma \delta}{\beta \gamma \delta \alpha}}$$ は $${\alpha\rightarrow\beta\rightarrow\gamma\rightarrow\delta\rightarrow\alpha}$$ と巡回する４つの文字の置換なので『４次巡回置換』となり、$${(\alpha \beta \gamma \delta)}$$ と表す。

$$
\begin{align*}
\dbinom{\alpha \beta \gamma \delta}{\beta \gamma \delta \alpha}
=(\alpha \beta \gamma \delta)
\end{align*}
$$

また５次置換 $${\dbinom{\alpha \beta \gamma \delta \epsilon}{\beta \gamma \delta \epsilon \alpha}}$$ は $${\alpha\rightarrow\beta\rightarrow\gamma\rightarrow\delta\rightarrow\epsilon\rightarrow\alpha}$$ と巡回する５つの文字の置換なので『５次巡回置換』となり、$${(\alpha \beta \gamma \delta \epsilon)}$$ と表す。

$$
\begin{align*}
\dbinom{\alpha \beta \gamma \delta \epsilon}{\beta \gamma \delta \epsilon \alpha}
=(\alpha \beta \gamma \delta \epsilon)
\end{align*}
$$

以上をまとめると、３次置換は以下のように簡潔に表記できる。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=I\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha \beta \gamma)
\end{rcases}遇置換\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

ここで２つ、４つなど、偶数個の互換の積で表せる置換を『遇置換』、１つ、３つなど、奇数個の互換の積で表せる置換を『奇置換』といったね。なお、何も変化しない恒等置換 $${I}$$ は、同じ２つの互換の積で表されるので遇置換となる。

$$
\begin{align*}
\dbinom{\alpha \beta \gamma}{\alpha \beta \gamma}=I=(\alpha \beta)(\alpha \beta)
\end{align*}
$$

先の３次置換では①～③が遇置換、④～➅が奇置換だったね。復習しておこうか（$${\Rightarrow}$$ 詳しくは本シリーズ (8)）。
　以下のように①～③は２つの互換の積で表せるので遇置換、④～➅は１つの互換の積で表せるので奇置換となる。なお、一般に互換の積の表し方は複数通りある場合がある。①～③の互換の積も１通りではなく複数通りあるが、ここでは代表で１通りだけを示しておくよ。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}遇置換\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}奇置換
\end{align*}
$$

　後々のために、ここで少し注意を入れておこう。それは
　『すべての遇置換は必ず３次巡回置換で表すことができる』
ということ。上の例で言うと①～③が遇置換なので、３次巡回置換で表せる。最初の説明のところで表したね。あっ①の恒等置換は表してはいないけど、同じ３次巡回置換を３回連続作用させれば元に戻るので、次のように書けるね。改めて遇置換をすべて３次巡回置換で表すと

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=(\alpha \beta \gamma)(\alpha \beta \gamma)(\alpha \beta \gamma)\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=(\alpha \gamma \beta)\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=(\alpha \beta \gamma)
\end{rcases}遇置換
\end{align*}
$$

①は同じ３次巡回置換 $${(\alpha \beta \gamma)}$$ を連続３回作用させるので、結局元に戻って同じになる。つまり作用させても何も変化しないので恒等置換 $${I}$$ と同じ。②と③は最初にやった３次巡回置換と同じだね。このように、すべての遇置換は３次巡回置換（およびその積）で表すことができるんだね。この事実は、後に５次以上の方程式に解の公式が存在しないことの証明で使うので、今のうちに押さえておこう。

3. 新しい表記法

　ここで、ある式 $${A}$$ に例えば置換 $${\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}}$$ を作用させることを、次のように表記する。

$$
\begin{align*}
&\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}A\\
&\hspace{21pt}\uparrow\hspace{26pt}\uparrow\\
&\hspace{17pt}{\small 置換}\hspace{17pt}{\small 式}
\end{align*}
$$

つまり、式の前に作用させたい置換を置く。今の場合、この置換は

$$
\begin{align*}
\dbinom{\alpha \beta \gamma}{\beta \gamma \alpha}
=(\alpha \beta \gamma)
\end{align*}
$$

と巡回置換で書けたので、次のように簡潔に表記できる。

$$
\begin{align*}
&(\alpha \beta \gamma)A\\
&\hspace{16pt}\uparrow\hspace{19pt}\uparrow\\
&\hspace{12pt}{\small 置換}\hspace{11pt}{\small 式}
\end{align*}
$$

例えば、差積 $${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ に巡回置換 $${(\alpha \beta \gamma)}$$ を作用させることは次のように表記できる。

$$
\begin{align*}
&(\alpha \beta \gamma)X_3\\
=\,&(\alpha \beta \gamma)\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}\\
&\hspace{16pt}\uparrow\hspace{69pt}\uparrow\\
&\hspace{12pt}{\small 置換}\hspace{61pt}{\small 式}
\end{align*}
$$

式は小カッコ $${(\hspace{14pt})}$$ で表されているので、外側を中カッコ $${\{\hspace{14pt}\}}$$ で囲っているよ。小カッコの外は中カッコで囲うんだね。さて復習も兼ねて実際に計算すると、巡回置換 $${(\alpha \beta \gamma)}$$ は $${\alpha}$$ を $${\gamma}$$ に、$${\beta}$$ を $${\alpha}$$ に、$${\gamma}$$ を $${\beta}$$ に置き換えるので

$$
\begin{align*}
(\alpha \beta \gamma)\{&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}\\
&\hspace{1.5pt}\downarrow\hspace{13pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow \hspace{9pt}\downarrow\hspace{13pt}\downarrow\\
=\,&(\gamma-\alpha)(\alpha-\beta)(\beta-\gamma)\\
=\,&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)
\hspace{2pt}\Leftarrow 変化しない
\end{align*}
$$

巡回置換 $${(\alpha \beta \gamma)}$$ は遇置換であったので、遇置換で対称性を保つ差積 $${X_3}$$ は変化しないんだね。
　同様に、ある式 $${A}$$ に例えば互換 $${(\beta \gamma)}$$ を作用させることは次のように表記できる。

$$
\begin{align*}
&(\beta \gamma)A\\
&\hspace{9pt}\uparrow\hspace{12pt}\uparrow\\
&\hspace{5pt}{\small 置換}\hspace{4pt}{\small 式}
\end{align*}
$$

例えば、差積 $${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ に互換 $${(\beta \gamma)}$$ を作用させると

$$
\begin{align*}
(\beta \gamma)\{&(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}\\
&\hspace{20pt}\downarrow\hspace{9pt}\downarrow\hspace{14pt}\downarrow\hspace{9pt}\downarrow\\
=\,&(\underline{\alpha-\gamma})(\gamma-\beta)(\underline{\underline{\beta-\alpha}})\\
=\,&(\underline{\underline{\beta-\alpha}})(\gamma-\beta)(\underline{\alpha-\gamma}) \Leftarrow (　　) を入れ替えた\\
=\,&(-\alpha+\beta)(-\beta+\gamma)(-\gamma+\alpha)\\
=\,&\{-(\alpha-\beta)\}\{-(\beta-\gamma)\}\{-(\gamma-\alpha)\}\\
=\,&(-1)^3(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\\
=\,&-(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha) \Leftarrow -1 倍と変化する
\end{align*}
$$

互換 $${(\beta \gamma)}$$ は奇置換であったので、差積 $${X_3}$$ は $${-1}$$ 倍と変化する。一般に $${X_3}$$ は遇置換でのみ対称性を保ち、奇置換では $${-1}$$ 倍と変化するんだね。($${\Rightarrow}$$ 証明は本シリーズ (9))

$$
X_3=
\begin{cases}
遇置換では対称性を保つ（変化しない）\\
奇置換では対称性が壊れている（-1 倍と変化する）
\end{cases}
$$

　今後の証明に備えて、今までの復習と必要な表記法を一通りやってみた。さてここからが本題だけど、森田君やってみる？」
　森田君は少し斜め上を見上げた後、決心したようにうなずいた。
「途中までしかできていませんが、やれるところまでやってみます」
　森田君はホワイトボードの前に立ち、黒のマーカーを手に取った。

4. ５次方程式について

「さて、ここからは次のような５次方程式を問題とします。
　$${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$
証明は背理法で行います（注３）。つまり「５次方程式に解の公式が存在する」と仮定し、矛盾することを示します。その矛盾は「５次方程式に解の公式が存在する」と仮定したことに由来するので、この仮定が間違っていることがわかり「５次方程式に解の公式が存在しない」ことが証明される、という論法です。
　では先ほどの５次方程式
　$${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$
に解の公式が存在すると仮定します。この両辺を $${x^5}$$ の係数 $${a(\ne0)}$$ で割って、$${x^5}$$ の係数を $${1}$$ にします。
　$${x^5+\dfrac{b}{a}x^4+\dfrac{c}{a}x^3+\dfrac{d}{a}x^2+\dfrac{e}{a}x+\dfrac{f}{a}=0}$$
ここで
　$${\dfrac{b}{a}=a_1, \dfrac{c}{a}=a_2, \dfrac{d}{a}=a_3, \dfrac{e}{a}=a_4, \dfrac{f}{a}=a_5}$$
と置いて
　$${x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0}$$
この５次方程式の５つの解を $${x_1, x_2, x_3, x_4, x_5}$$ とします。これは、もとの５次方程式
　$${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$
の解でもあります。両辺を $${x^5}$$ の係数 $${a(\ne0)}$$ で割っただけなので、解は変化しません。

$$
\begin{align*}
&ax^5+bx^4+cx^3+dx^2+ex+f=0\\
\xtofrom[\times a]{\div a} &x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0
\end{align*}
$$

　なお方程式の解を、今まではギリシャ文字で表していました。例えば３次方程式の解の導出では、$${x^3+px+q=0}$$ の解を $${\alpha, \beta, \gamma}$$ と置きました。５次方程式の場合、その解をギリシャ文字 $${\alpha, \beta, \gamma, \delta, \epsilon}$$ と置くことも可能ですが、これからは簡単のため、５次方程式の解を $${x_1, x_2, x_3, x_4, x_5}$$ と置きます。ひとつひとつの解は添え字の数字で区別します。文字ではなく数字で区別できるので、個数が多くなるとこの表記の方が考えやすくなります。

　ここで＜５次方程式の解と係数の関係＞を考えます。その一般形は次のようなものです。

5. ５次方程式の解と係数の関係

　$${ax^5+bx^4+cx^3+dx^2+ex+f=0}$$ の解を $${x_1, x_2, x_3, x_4, x_5}$$ とすると

$$
\begin{align*}
x_1+x_2+x_3+x_4+x_5&=-\dfrac{b}{a}\\
x_1x_2+x_1x_3+x_1x_4+x_1x_5+x_2x_3+x_2x_4+x_2x_5&\\
+x_3x_4+x_3x_5+x_4x_5&=\dfrac{c}{a}\\
x_1x_2x_3+x_1x_2x_4+x_1x_2x_5+x_1x_3x_4+x_1x_3x_5+x_1x_4x_5&\\
+x_2x_3x_4+x_2x_3x_5+x_2x_4x_5+x_3x_4x_5&=-\dfrac{d}{a}\\
x_1x_2x_3x_4+x_1x_2x_3x_5+x_1x_2x_4x_5+x_1x_3x_4x_5
+x_2x_3x_4x_5&=\dfrac{e}{a}\\
x_1x_2x_3x_4x_5&=-\dfrac{f}{a}
\end{align*}
$$

これらの式の左辺は、５変数の『基本対称式』のすべてのセットです。具体的に見ていきますと
　１行目は解のすべての和
　２行目はは２つずつの解の積のすべての和
　３行目は３つずつの解の積のすべての和
　４行目は４つずつの解の積のすべての和
　５行目は５つの解の積
となり、これらは５変数の基本対称式のすべてとなります。この＜解と係数の関係＞を、$${x^5}$$ の係数を $${1}$$ にした５次方程式
　$${x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0}$$
に適用すると
　$${a=1, b=a_1, c=a_2, d=a_3, e=a_4, f=a_5}$$
となるので

$$
\begin{align*}
x_1+x_2+x_3+x_4+x_5&=-\dfrac{a_1}{1}\\
x_1x_2+x_1x_3+x_1x_4+x_1x_5+x_2x_3+x_2x_4+x_2x_5&\\
+x_3x_4+x_3x_5+x_4x_5&=\dfrac{a_2}{1}\\
x_1x_2x_3+x_1x_2x_4+x_1x_2x_5+x_1x_3x_4+x_1x_3x_5+x_1x_4x_5&\\
+x_2x_3x_4+x_2x_3x_5+x_2x_4x_5+x_3x_4x_5&=-\dfrac{a_3}{1}\\
x_1x_2x_3x_4+x_1x_2x_3x_5+x_1x_2x_4x_5+x_1x_3x_4x_5+x_2x_3x_4x_5&=\dfrac{a_4}{1}\\
x_1x_2x_3x_4x_5&=-\dfrac{a_5}{1}
\end{align*}
$$

より

$$
\begin{align*}
x_1+x_2+x_3+x_4+x_5&=-a_1\\
x_1x_2+x_1x_3+x_1x_4+x_1x_5+x_2x_3+x_2x_4+x_2x_5&\\
+x_3x_4+x_3x_5+x_4x_5&=a_2\\
x_1x_2x_3+x_1x_2x_4+x_1x_2x_5+x_1x_3x_4+x_1x_3x_5+x_1x_4x_5&\\
+x_2x_3x_4+x_2x_3x_5+x_2x_4x_5+x_3x_4x_5&=-a_3\\
x_1x_2x_3x_4+x_1x_2x_3x_5+x_1x_2x_4x_5+x_1x_3x_4x_5+x_2x_3x_4x_5&=a_4\\
x_1x_2x_3x_4x_5&=-a_5
\end{align*}
$$

よって

$$
\begin{align*}
a_1&=-(x_1+x_2+x_3+x_4+x_5)\\
a_2&=x_1x_2+x_1x_3+x_1x_4+x_1x_5+x_2x_3+x_2x_4+x_2x_5\\
&+x_3x_4+x_3x_5+x_4x_5\\
a_3&=-(x_1x_2x_3+x_1x_2x_4+x_1x_2x_5+x_1x_3x_4+x_1x_3x_5+x_1x_4x_5\\
&+x_2x_3x_4+x_2x_3x_5+x_2x_4x_5+x_3x_4x_5)\\
a_4&=x_1x_2x_3x_4+x_1x_2x_3x_5+x_1x_2x_4x_5+x_1x_3x_4x_5+x_2x_3x_4x_5\\
a_5&=-x_1x_2x_3x_4x_5
\end{align*}
$$

となり、５次方程式の係数 $${a_1, a_2, a_3, a_4, a_5}$$ は５変数の基本対称式、または基本対称式の $${-1}$$ 倍です。すると
　「すべての対称式は基本対称式の加減乗除で表せる」
という＜対称式の基本定理＞及びその逆命題
　「基本対称式の加減乗除で表せる式はすべて対称式である」
により、基本対称式（及びその $${-1}$$ 倍）の加減乗除で表せる式はすべて対称式です。対称式を定数倍しても対称式なので、基本対称式の $${-1}$$ 倍（定数倍）である $${a_1, a_3, a_5}$$ を構成要素に入れても問題ありません。対称式は必ず $${a_1, a_2, a_3, a_4, a_5}$$ の加減乗除で表すことができ、逆に $${a_1, a_2, a_3, a_4, a_5}$$ の加減乗除で表せる式は、すべて対称式となります。
　すると、係数 $${a_1, a_2, a_3, a_4, a_5}$$ の加減乗除だけでは解の公式を導き出すことはできないことになります。２次や３次方程式でもやったように、解の式 $${x_1, x_2, x_3, x_4, x_5}$$ は対称式ではないからです。

$$
\begin{align*}
\underbrace{x_1}_{対称式でない}\hspace{-14pt}
&\ne\underbrace{（係数 a_1, a_2, a_3, a_4, a_5 で表す）}_{加減乗除では対称式}\\
\underbrace{x_2}_{対称式でない}\hspace{-14pt}
&\ne\underbrace{（係数 a_1, a_2, a_3, a_4, a_5 で表す）}_{加減乗除では対称式}\\
&\hspace{5pt}\vdots\\
\underbrace{x_5}_{対称式でない}\hspace{-14pt}
&\ne\underbrace{（係数 a_1, a_2, a_3, a_4, a_5 で表す）}_{加減乗除では対称式}
\end{align*}
$$

解の式 $${x_1, x_2, x_3, x_4, x_5}$$ を変化させない置換、つまり $${x_1, x_2, x_3, x_4, x_5}$$ の対称性を保つ置換は恒等置換のみです。よって解の公式の導出には、恒等置換でのみ対称性を保つ式を作る必要があります。（$${\Rightarrow}$$ 詳しくは本シリーズ (11), (12), (13)）

6. ５次置換について

　ここで、５次方程式には解の公式が存在しないことの証明に備えて、新たに５次置換を考えます。３次置換とは３つの文字の入れ替えでした。５次置換とは５つの文字の入れ替えとなります。ここでは５次方程式
　$${x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0}$$
の５つの解 $${x_1, x_2, x_3, x_4, x_5}$$ の置換を考えます。例えば $${x_1}$$ を $${x_3}$$ に、$${x_2}$$ を $${x_5}$$ に、$${x_3}$$ を $${x_1}$$ に、$${x_4}$$ を $${x_2}$$ に、$${x_5}$$ を $${x_4}$$ に置き換える置換

$$
\begin{align*}
x_1 \longrightarrow x_3\\
x_2 \longrightarrow x_5\\
x_3 \longrightarrow x_1\\
x_4 \longrightarrow x_2\\
x_5 \longrightarrow x_4
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
x_3 & x_5 & x_1 & x_2 & x_4
\end{pmatrix}
$$

と表します。これまでと同じように、カッコの中の文字は上から下へ置換すると考えます。すると、次の５次置換は置換しても変化しないので恒等置換 $${I}$$ となります。

$$
\begin{align*}
\dbinom{x_1 x_2 x_3 x_4 x_5}{x_1 x_2 x_3 x_4 x_5}=I
\end{align*}
$$

次の置換は $${x_1}$$ と $${x_2}$$ の入れ替えなので互換 $${(x_1 x_2)}$$ と表すことができます。下線部の文字だけが入れ替わっています。他は変化していません。

$$
\begin{align*}
\dbinom{\underline{x_1 x_2} x_3 x_4 x_5}{\underline{x_2 x_1} x_3 x_4 x_5}=(x_1 x_2)
\end{align*}
$$

これは１個の互換で表せるので奇置換です。奇置換は奇数個の互換で表せる置換でした。
　また、次の置換は $${x_1}$$ と $${x_2}$$ の入れ替え、かつ $${x_3}$$ と $${x_4}$$ の入れ替えなので互換 $${(x_1 x_2)(x_3 x_4)}$$ と表すことができます。１重線部の文字と２重線部の文字が入れ替わっています。他は変化していません。

$$
\begin{align*}
\dbinom{\underline{x_1 x_2} \underline{\underline{x_3 x_4}} x_5}{\underline{x_2 x_1} \underline{\underline{x_4 x_3}} x_5}=(x_1 x_2)(x_3 x_4)
\end{align*}
$$

これは２個の互換で表せるので遇置換です。遇置換は遇数個の互換で表せる置換でした。
　また、次の置換は $${x_1\rightarrow x_2\rightarrow x_3\rightarrow x_1}$$ と巡回する置換なので、３次巡回置換となり $${(x_1 x_2 x_3)}$$ と表すことができます。下線部の文字が循環的に入れ替わっています。他は変化していません。

$$
\begin{align*}
\dbinom{\underline{x_1 x_2 x_3} x_4 x_5}{\underline{x_2 x_3 x_1} x_4 x_5}=(x_1 x_2 x_3)
\end{align*}
$$

またこの５次置換は、次のような２つの互換の積
　$${(x_2 x_3)(x_1 x_2)}$$
で表すことができます。以下それを示します。なおこのシリーズでは、互換の積は左から（前から）順に作用させていくと定義しました。よって $${(x_2 x_3)(x_1 x_2)}$$ は、先に $${(x_2 x_3)}$$ を作用させてから、次に $${(x_1 x_2)}$$ を作用させます。

$$
\begin{align*}
x_1 x_2 &x_3 x_4 x_5\\
&\Downarrow 置換 (x_2 x_3)\\
x_1 x_3 &x_2 x_4 x_5\\
&\Downarrow 置換 (x_1 x_2)\\
x_2 x_3 &x_1 x_4 x_5
\end{align*}
$$

よって

$$
\begin{align*}
x_1 x_2 &x_3 x_4 x_5\\
&\Downarrow 置換 (x_2 x_3)(x_1 x_2)\\
x_2 x_3 &x_1 x_4 x_5
\end{align*}
$$

この置換は先ほどの $${\dbinom{x_1 x_2 x_3 x_4 x_5}{x_2 x_3 x_1 x_4 x_5}=(x_1 x_2 x_3)}$$ と同じなので、この置換は

$$
\begin{align*}
\dbinom{x_1 x_2 x_3 x_4 x_5}{x_2 x_3 x_1 x_4 x_5}&=(x_1 x_2 x_3)\\
&=(x_2 x_3)(x_1 x_2)
\end{align*}
$$

と２つの互換の積 $${(x_2 x_3)(x_1 x_2)}$$ で表すことができます。２つ（偶数個）の互換の積なので、この置換は遇置換となります。

　ここで５次置換のすべての個数を考えます。

7. ５次置換のすべての個数を数える

　５次置換は一般に、次のように表せます。

$$
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
〇 & △ & \square & ♢ & ♡
\end{pmatrix}
$$

この $${〇, △, \square, ♢, ♡}$$ には $${x_1, x_2, x_3, x_4, x_5}$$ の５つの文字のいずれかが入ります。ただし重複せずにそれぞれ別々の文字が入り、同じ文字が２か所以上に入ることはありません。まず左側の〇から決めていきます。〇には $${x_1, x_2, x_3, x_4, x_5}$$ の５通りうち、いずれかの文字が入ります。

$$
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
〇 & △ & \square & ♢ & ♡
\end{pmatrix}\\
{\uparrow \atop \footnotesize{５通り}}\hspace{80pt}
$$

ここで、仮に〇が $${x_1}$$ だとします。

$$
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
x_1 & △ & \square & ♢ & ♡
\end{pmatrix}
$$

すると△には $${x_1}$$ 以外、つまり $${x_2, x_3, x_4, x_5}$$ の４通りのうち、いずれかの文字が入ります。

$$
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
x_1 & △ & \square & ♢ & ♡
\end{pmatrix}\\
{\uparrow \atop \footnotesize{４通り}}\hspace{40pt}
$$

仮に△が $${x_2}$$ だとします。

$$
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
x_1 & x_2 & \square & ♢ & ♡
\end{pmatrix}
$$

すると $${\square}$$ には $${x_1, x_2}$$ 以外、つまり $${x_3, x_4, x_5}$$ の３通りのうち、いずれかの文字が入ります。

$$
\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
x_1 & x_2 & \square & ♢ & ♡
\end{pmatrix}\\
{\uparrow \atop \footnotesize{３通り}}\hspace{0.5pt}
$$

このように考えていくと、$${〇, △, \square, ♢, ♡}$$ の文字の入れ方は
　$${5\times4\times3\times2\times1=120}$$ 通り
となります。

$$
\begin{align*}
&\begin{pmatrix}
x_1 & x_2 & x_3 & x_4 & x_5\\
〇 & △ & \square & ♢ & ♡
\end{pmatrix}\\
&\hspace{9pt}\uparrow\hspace{15pt}\uparrow\hspace{15pt}\uparrow\hspace{15pt}\uparrow\hspace{15pt}\uparrow\\
&\hspace{12pt}5\hspace{1.2pt}\times\hspace{1.2pt}4\hspace{1.2pt}\times\hspace{1.3pt}3\hspace{1.3pt}\times\hspace{1.3pt}2\hspace{1.3pt}\times\hspace{1.3pt}1=120 通り
\end{align*}
$$

これは５つの文字 $${x_1, x_2, x_3, x_4, x_5}$$ を１列に並べる並べ方の総数と同じです。復習として、２次置換の総数は $${\alpha, \beta}$$ を１列に並べる並べ方の総数と同じなので $${2\times1=2}$$ 通りです。

$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta\\
〇 & △
\end{pmatrix}\\
&\hspace{9pt}\uparrow\hspace{15pt}\uparrow\\
&\hspace{12pt}2\hspace{1.2pt}\times\hspace{1.2pt}1=2 通り
\end{align*}
$$

３次置換の総数は $${\alpha, \beta, \gamma}$$ を１列に並べる並べ方の総数と同じなので $${3\times2\times1=6}$$ 通りです。

$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta & \gamma\\
〇 & △ & \square
\end{pmatrix}\\
&\hspace{9pt}\uparrow\hspace{14pt}\uparrow\hspace{14pt}\uparrow\\
&\hspace{12pt}3\hspace{1.1pt}\times\hspace{1.1pt}2\hspace{1.1pt}\times\hspace{1.1pt}1=6 通り
\end{align*}
$$

すると、４次置換の総数は $${\alpha, \beta, \gamma, \delta}$$ の４つの文字を１列に並べる並べ方の総数と同じなので
　$${4\times3\times2\times1=24}$$ 通り
そして先ほどやったように５次置換の総数は $${120}$$ 通りと、文字が多くなるにつれて、その総数は急激に増大していきます。

　ここで $${n}$$ 次置換について、一般に次の定理が成り立ちます（証明は略）。

＜『$${\boldsymbol{n}}$$ 次置換』についての定理（復習）＞

（定理Ⅰ）すべての $${n}$$ 次置換は、１つの互換、または複数の互換の積で表すことができる。
　例えば次の３次置換①～➅について、①～③は２つの互換の積、④～⑥は１つの互換で表される。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}２つの互換の積\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}１つの互換
\end{align*}
$$

（定理Ⅱ）ある $${n}$$ 次置換について、その置換が遇置換になるか、奇置換になるかはあらかじめ決まっている。つまり、ある $${n}$$ 次置換が、互換の選び方によって遇置換になったり奇置換になったりすることはない。

　例えば先ほどの３次置換①～➅について、①～③は必ず遇置換で奇置換になることはなく、④～➅は必ず奇置換で遇置換になることはない。なお①～③は複数ある互換の積のうち、代表で１つの互換の積を選んだ。互換の積の表し方は必ずしも１通りとは限らず、複数通りある場合がある。

（定理Ⅲ）$${n}$$ 次置換について、遇置換と奇置換に分けたときに、そのときの遇置換と奇置換の個数はもとの置換の２分の１で、互いに同じ個数となる。
　例えば先ほどの６つの３次置換について、遇置換は①～③の３つ、奇置換は④～➅の３つで、ちょうど半分ずつ、同じ数ずつ振り分けられる。例えば遇置換が４つ、奇置換が２つのようにはならず、遇置換と奇置換の個数はきっちりと半分ずつに分かれる。

$$
\begin{align*}
&\begin{rcases}
➀\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \beta & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}\\
\\
②\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \alpha & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\gamma & \alpha
\end{pmatrix}\\
\\
③\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \gamma & \alpha
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}
\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}３通り\\
\\
&\begin{rcases}
④\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\alpha & \gamma & \beta
\end{pmatrix}
=\begin{pmatrix}
\beta & \gamma
\end{pmatrix}\\
\\
⑤\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\gamma & \beta & \alpha
\end{pmatrix}
=\begin{pmatrix}
\alpha & \gamma
\end{pmatrix}\\
\\
⑥\hspace{6pt}
\begin{pmatrix}
\alpha & \beta & \gamma\\
\beta & \alpha & \gamma
\end{pmatrix}
=\begin{pmatrix}
\alpha & \beta
\end{pmatrix}
\end{rcases}３通り
\end{align*}
$$

これらの定理は $${n=5}$$ のとき、つまり５次置換についても成り立ちます。よって５次置換は必ず１つ、または複数の互換の積で表すことができ（定理Ⅰ）、さらに遇置換か奇置換かはあらかじめ決まっていて（定理Ⅱ）、その個数はちょうど半分ずつに分かれます（定理Ⅲ）。すると５次置換の総数は $${120}$$ 通りだったので、遇置換はちょうどその半分の $${60}$$ 通りとなります。

$$
５次置換 120 通り
\begin{cases}
遇置換 60 通り（半分）\\
奇置換 60 通り（半分）
\end{cases}
$$

8. ５つの解の『差積』の添加

　ここで、前回３次方程式の解の導出でやった、解の式 $${X}$$ の「条件Ⅰ」について、その「条件Ⅰ」の５次置換のバージョンを考えます。（$${\Rightarrow}$$ 詳しくは本シリーズ (12)）

$${\boldsymbol{X}}$$ の「条件Ⅰ」（５次置換バージョン）
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は５次置換で対称性が壊れているが、$${X^2}$$ では５次置換で対称性を保つ。』（注４）
　なお言葉として、「ある置換で式が変化する」ことを「対称性が壊れている」、「ある置換で式が変化しない」ことを「対称性を保つ」と表現することがあります。
（例）
　差積 $${(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ は奇置換では対称性が壊れているが、遇置換では対称性を保つ。

　さてこの「条件Ⅰ」を満たす $${X}$$ が、解を用いて作れるのかどうかを考えます。２次方程式のバージョンでは、 $${x^2+a_1x+a_2=0}$$ の２つの解を $${\alpha, \beta}$$ としたときの差積
　$${X_2=\alpha-\beta}$$
として $${X}$$ を作れました。３次方程式のバージョンでは、$${y^3+px+q=0}$$ の３つの解を $${\alpha, \beta, \gamma}$$ としたときの差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
として $${X}$$ を作れました。（$${\Rightarrow}$$ 詳しくは本シリーズ (12)）
　するとその拡張として、５次方程式でも差積を考えます。つまり、$${x^5+a_1x^4+a_2x^3+a_3x^2+a_2x+a_4=0}$$ の５つの解を $${x_1, x_2, x_3, x_4, x_5}$$ としたときの差積

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

として $${X}$$ を作ることができます。なおここでは、添え字の数字 $${1, 2, 3, 4, 5}$$ について辞書式（小さい順）に引いていくと定義します。５つの解 $${x_1, x_2, x_3, x_4, x_5}$$ は対等で区別が無いので「５つの解の差のすべての組み合わせの積」となっていれば、どのような順番で定義しても問題ありません。
　するとこの $${X_5}$$ は、奇置換では $${-1}$$ 倍と変化し対称性が壊れていますが、遇置換では変化せず対称性を保っています。実際に計算してます。まず差積 $${X_5}$$ に奇置換である互換 $${(x_1 x_2)}$$ を作用させてみます。先ほど習った表記法を用いてみますと

$$
\begin{align*}
置換\hspace{87pt}式\hspace{75pt}&\\
\downarrow\hspace{96pt}\downarrow\hspace{77pt}&\\
(x_1 x_2)X_5=(x_1 x_2)\{(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&\}\\
=\hspace{40pt}
(\underbrace{x_2-x_1})(\underline{x_2-x_3})(\underline{\underline{x_2-x_4}})(\underline{\underline{\underline{x_2-x_5}}})&\\
\cdot\,(\underline{x_1-x_3})(\underline{\underline{x_1-x_4}})(\underline{\underline{\underline{x_1-x_5}}})&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

$${\underbrace{\hspace{15pt}}}$$ 部分は $${-1}$$ でくくり、１重線同士、２重線同士、３重線同士を入れ替えると

$$
\begin{alignat*}{2}
(x_1 x_2)X_5&=\hspace{34pt} &
\underbrace{-(x_1-x_2)}(\underline{x_1-x_3})(\underline{\underline{x_1-x_4}})(\underline{\underline{\underline{x_1-x_5}}})&\\
& & \cdot\,(\underline{x_2-x_3})(\underline{\underline{x_2-x_4}})(\underline{\underline{\underline{x_2-x_5}}})&\\
& & \cdot\,(x_3-x_4)(x_3-x_5)&\\
& & \cdot\,(x_4-x_5)\\
&=-X_5 & &
\end{alignat*}
$$

この式変形をよく眺めてみると、１重線、２重線、３重線部分は順番が入れ変わるだけで変化せず、$${\underbrace{\hspace{15pt}}}$$ 部分の $${-1}$$ 倍の影響だけが残り、置換後は $${-1}$$ 倍となっていることがわかります。つまり互換 $${(x_1 x_2)}$$ を作用させた場合、同じ文字の差である $${(\underbrace{x_1-x_2})}$$ の、$${x_1, x_2}$$ の入れ替えによって生じる $${-1}$$ 倍の影響だけが残るわけです。

$$
\begin{align*}
X_5 \xrightarrow[(x_1 x_2)]{} -X_5
\end{align*}
$$

　また、差積 $${X_5}$$ に互換 $${(x_2 x_4)}$$ を作用させてみます。

$$
\begin{align*}
(x_2 x_4)X_5=(x_1 x_2)\{(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&\}\\
=\hspace{40pt}
(\underline{x_1-x_4})(x_1-x_3)(\underline{x_1-x_2})(x_1-x_5)&\\
\cdot\,(\undergroup{x_4-x_3})(\underbrace{x_4-x_2})(\underline{\underline{x_4-x_5}})&\\
\cdot\,(\undergroup{x_3-x_2})(x_3-x_5)&\\
\cdot\,(\underline{\underline{x_2-x_5}})&
\end{align*}
$$

$${\underbrace{\hspace{15pt}}}$$ と $${\undergroup{\hspace{15pt}}}$$ 部分は $${-1}$$ でくくり、１重線同士、２重線同士を入れ替えると

$$
\begin{align*}
(x_2 x_4)X_5=\hspace{40pt}
(\underline{x_1-x_2})(x_1-x_3)(\underline{x_1-x_4})(x_1-x_5)&\\
\cdot\,\{\undergroup{-(x_3-x_4)}\}\{\underbrace{-(x_2-x_4)}\}(\underline{\underline{x_2-x_5}})&\\
\cdot\,\{\undergroup{-(x_2-x_3)}\}(x_3-x_5)&\\
\cdot\,(\underline{\underline{x_4-x_5}})&
\end{align*}
$$

２つある $${\undergroup{\hspace{15pt}}}$$ 部分では、$${-1}$$ 倍の２つ分を掛けて $${(-1)^2=1}$$ 倍となるので変化せず、さらに $${\undergroup{\hspace{15pt}}}$$ 同士を入れ替えて

$$
\begin{align*}
(x_2 x_4)X_5=\hspace{40pt}
(\underline{x_1-x_2})(x_1-x_3)(\underline{x_1-x_4})(x_1-x_5)&\\
\cdot\,(\undergroup{x_3-x_4})\{\underbrace{-(x_2-x_4)}\}(\underline{\underline{x_2-x_5}})&\\
\cdot\,(\undergroup{x_2-x_3})(x_3-x_5)&\\
\cdot\,(\underline{\underline{x_4-x_5}})&\\
=\hspace{40pt}
(\underline{x_1-x_2})(x_1-x_3)(\underline{x_1-x_4})(x_1-x_5)&\\
\cdot\,(\undergroup{x_2-x_3})\{\underbrace{-(x_2-x_4)}\}(\underline{\underline{x_2-x_5}})&\\
\cdot\,(\undergroup{x_3-x_4})(x_3-x_5)&\\
\cdot\,(\underline{\underline{x_4-x_5}})&
\end{align*}
$$

１重線部、２重線部、$${\undergroup{\hspace{15pt}}}$$ 部分は順番が入れ変わるだけで変化せず、$${\underbrace{\hspace{15pt}}}$$ 部分の $${-1}$$ 倍の影響だけが残り、置換後は $${-1}$$ 倍となります。

$$
\begin{alignat*}{2}
(x_2 x_4)X_5&=\hspace{35pt} &
-(\underline{x_1-x_2})(x_1-x_3)(\underline{x_1-x_4})(x_1-x_5)&\\
& & \cdot\,(\undergroup{x_2-x_3})(\underbrace{x_2-x_4})(\underline{\underline{x_2-x_5}})&\\
& & \cdot\,(\undergroup{x_3-x_4})(x_3-x_5)&\\
& & \cdot\,(\underline{\underline{x_4-x_5}})&\\
&=-X_5
\end{alignat*}
$$

つまり互換 $${(x_2 x_4)}$$ を作用させた場合、先ほどと同じように同じ文字の差である $${(\underbrace{x_2-x_4})}$$ の、$${x_2, x_4}$$ の入れ替えによって生じる $${-1}$$ 倍の影響だけが残るわけです。

$$
\begin{align*}
X_5 \xrightarrow[(x_2 x_4)]{} -X_5
\end{align*}
$$

一般に２変数 $${X_2}$$、３変数 $${X_2}$$、４変数 $${X_4}$$、５変数 $${X_5}$$、$${\cdots}$$ と、何変数の差積でも１つの互換を作用させると $${-1}$$ 倍と変化します。例えば差積 $${X_2, X_3, X_4, X_5、\cdots}$$ に、任意の１つの互換 $${(x_i x_j)}$$ を作用させると
　$${(x_i x_j)X_2=-X_2}$$
　$${(x_i x_j)X_3=-X_3}$$
　$${(x_i x_j)X_4=-X_4}$$
　$${(x_i x_j)X_5=-X_5}$$
$${\hspace{50pt}\vdots}$$
つまり、一般に $${n}$$ 変数の差積 $${X_n}$$ について
　$${(x_i x_j)X_n=-X_n}$$
となり、任意の１つの互換を作用させると、$${X_n}$$ は $${-X_n}$$ と $${-1}$$ 倍に変化します。

$$
\begin{align*}
X_n \xrightarrow[(x_i x_j)]{} -X_n
\end{align*}
$$

　それでは、互換を２回作用させるとどうなるでしょうか。例えば
　$${(x_1 x_2)(x_2 x_4)}$$
を $${X_5}$$ に作用させてみます。なお互換は左から（前から）順に作用させると定義したので、先に $${(x_1 x_2)}$$ を作用させてから、次に $${(x_2 x_4)}$$ を作用させます。すると最初の互換 $${(x_1 x_2)}$$ で $${-1}$$ 倍と変化し、次の互換 $${(x_2 x_4)}$$ でさらに $${-1}$$ 倍となるので結局 $${(-1)^2=1}$$ 倍となり、変化しないことがわかります。

$$
\begin{align*}
X_5 &\xrightarrow[(x_1 x_2)]{} -X_5\\
&\xrightarrow[(x_2 x_4)]{} -(-X_5)=(-1)^2X_5=X_5
\end{align*}
$$

つまり

$$
\begin{align*}
X_5 &\xrightarrow[(x_1 x_2)(x_2 x_4)]{} X_5 \Rightarrow 変化しない
\end{align*}
$$

一般に、$${n}$$ 変数の差積 $${X_n}$$ に任意の２つの互換の積 $${(x_i x_j)(x_k x_l)}$$ を作用させても $${X_n}$$ は変化しません。

$$
\begin{align*}
X_n \xrightarrow[(x_i x_j)(x_k x_l)]{} X_n \Rightarrow 変化しない
\end{align*}
$$

このことはさらに一般化できて、$${X_n}$$ は任意の遇置換（偶数個の互換の積）を作用させると変化しませんが、任意の奇置換（奇数個の互換の積）を作用させると $${-1}$$ 倍と変化します。

$$
\begin{align*}
&X_n \xrightarrow[遇置換]{} X_n \Rightarrow 変化しない\\
&X_n \xrightarrow[奇置換]{} -X_n \Rightarrow 変化する（-1 倍）
\end{align*}
$$

ここで改めて、先ほど述べた解の式 $${X}$$ の「条件Ⅰ」を考えてみます。

$${\boldsymbol{X}}$$ の「条件Ⅰ」（５次置換バージョン）
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は５次置換で対称性が壊れているが、$${X^2}$$ では５次置換で対称性を保つ。』

すると、この条件を満たす $${X}$$ は差積 $${X_5}$$

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

であることがわかります。この条件の $${X}$$ を $${X_5}$$ で置き換えてみると

　『$${X_5}$$ は対称式ではないが、$${(X_5)^2}$$ は対称式である。』
詳しく言うと
　『$${X_5}$$ は５次置換で対称性が壊れているが、$${(X_5)^2}$$ では５次置換で対称性を保つ。』

確認して見ます。まず $${X_5}$$ は対称式でありません。$${X_5}$$ は遇置換では変化しませんが、奇置換では変化するからです。

$$
\begin{align*}
&X_5 \xrightarrow[遇置換]{} X_5 \Rightarrow 変化しない\\
&X_5 \xrightarrow[奇置換]{} -X_5 \Rightarrow 変化する（-1 倍）
\end{align*}
$$

つまり、$${X_5}$$ は５次置換では対称性が壊れています。一方２乗した $${(X_5)^2}$$

$$
\begin{align*}
(X_5)^2=\{(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&\}^2
\end{align*}
$$

は対称式となります。遇置換では変化しませんが、奇置換でも $${(-1)^2=1}$$ 倍となるので変化しないからです。

$$
\begin{align*}
&(X_5)^2 \xrightarrow[遇置換]{} (X_5)^2 \Rightarrow 変化しない\\
&(X_5)^2 \xrightarrow[奇置換]{} (-X_5)^2=(X_5)^2 \Rightarrow 変化しない
\end{align*}
$$

つまり、５次置換で $${(X_5)^2}$$ は対称性を保ちます。

$$
\begin{align*}
(X_5)^2 \xrightarrow[５次置換]{} (X_5)^2 \Rightarrow &変化しない
\end{align*}
$$

よって $${(X_5)^2}$$ は対称式となり、５次置換で対称性を保ちます。以上より、この「条件Ⅰ」を満たす $${X}$$ は差積 $${X_5}$$ となります。「条件Ⅰ」満たすを解の式 $${X}$$ を、差積 $${X_5}$$ として作ることができたわけです。

　ここで添加を考えます。先ほどやった＜５次方程式の解と係数の関係＞より、５次方程式
　$${x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0}$$
の係数 $${a_1, a_2, a_3, a_4, a_5}$$ は、次のように基本対称式、または基本対称式を $${-1}$$ 倍したものでした。

ここで、係数 $${a_1, a_2, a_3, a_4, a_5}$$ と、$${1}$$ の３乗根 $${\omega}$$ の加減乗除で表される式の集合を $${Q(\omega)}$$ とします。すると＜対称式の基本定理＞より、基本対称式（及びその $${-1}$$ 倍）である
　$${a_1, a_2, a_3, a_4, a_5}$$
の加減乗除で表せる式はすべて対称式なので、集合 $${Q(\omega)}$$ は対称式の集合です。対称式を定数倍しても対称式ですので、基本対称式の $${-1}$$ 倍（定数倍）である $${a_1, a_3, a_5}$$ が構成要素に入っていても問題ありません。
　また $${1}$$ の３乗根のうち虚数である $${\omega}$$ も定数であるので、対称式を定数倍しても対称式であることから $${\omega}$$ を加減乗除に加えても問題ありません。いずれにせよ $${Q(\omega)}$$ は対称式の集合となります。
　すると、差積の２乗 $${(X_5)^2}$$ は対称式でした。よってこの集合 $${Q(\omega)}$$ 内では、対称式である $${(X_5)^2}$$ を $${a_1, a_2, a_3, a_4, a_5}$$ の加減乗除で表すことができます。

$$
\begin{align*}
(X_5)^2 &\Longrightarrow a_1, a_2, a_3, a_4, a_5 の加減乗除で表せる
\end{align*}
$$

　しかし、その平方根である $${\sqrt{(X_5)^2}}$$ は $${a_1, a_2, a_3, a_4, a_5}$$ の加減乗除で表すことはできません。平方（２乗）は２回掛ければ表現できますが、平方根を取る操作は加減乗除では表現できないからです。

$$
\begin{align*}
(X_5)^2 &\Longrightarrow a_1, a_2, a_3, a_4, a_5 の加減乗除で表せる\\
\sqrt{(X_5)^2} &\Longrightarrow a_1, a_2, a_3, a_4, a_5 の加減乗除で表せない
\end{align*}
$$

　そこで、$${Q(\omega)}$$ に $${\sqrt{(X_5)^2}}$$

$$
\begin{align*}
\sqrt{(X_5)^2}=\sqrt{\{(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)}&\\
\overline{\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)}&\\
\overline{\cdot\,(x_3-x_4)(x_3-x_5)}&\\
\overline{\cdot\,(x_4-x_5)\}^2}&
\end{align*}
$$

を添加し、その拡大された式の集合を
　$${Q(\omega, \sqrt{(X_5)^2})}$$
とします。$${Q(\omega, \sqrt{(X_5)^2})}$$ は、$${a_1, a_2, a_3, a_4, a_5}$$ と $${\omega}$$ と $${\sqrt{(X_5)^2}}$$ の加減乗除で表される式を含みます。$${Q(\omega)}$$ の世界では解の公式は構成できませんが、その新しい式 $${\sqrt{(X_5)^2}}$$ を加減乗除の対象として加えることによって使える式（道具）が拡大されます。$${\sqrt{(X_5)^2}}$$ は、係数 $${a_1, a_2, a_3, a_4, a_5}$$ の加減乗除で表現できる対称式の平方根なので、平方根という新しい道具が使えるようになった。解の公式を構成するためには、（整数のような我々が普通に使っている数と）もともとの方程式の係数と定数 $${\omega}$$ 、および「新たに添加された式（や定数）」の加減乗除によって解の公式が表現できるようになるまで、添加によって使える式の世界を拡大していくわけです。

$$
\begin{rcases}
{\small ① もともとの方程式の係数}\\
{\small ② 定数 \omega（３乗して 1 になる複素数）}\\
{\small ③ 整数など我々が普通に使っている数}
\end{rcases}
\Rightarrow
{\small 解の公式を構成できない}
$$

しかし

$$
\begin{rcases}
{\small ① もともとの方程式の係数}\\
{\small ② 定数 \omega（３乗して１になる複素数）}\\
{\small ③ 整数など我々が普通に使っている数}\\
{\small ④ 対称式の２乗の平方根 \sqrt{(X_5)^2} を添加}\\
{\small ⑤ 必要に応じて次々と式（や定数）を添加}\\
\hspace{60pt}{\small \vdots}
\end{rcases}
\Rightarrow
{\small 解の公式が構成可能となる}
$$

　ちなみに２次方程式では

$$
\begin{rcases}
{\small ① もともとの方程式の係数}\\
{\small ② 整数など我々が普通に使っている数}\\
{\small ③ 差積 X_2=\alpha-\beta} を添加
\end{rcases}
\Rightarrow
{\small 解の公式が構成できた}
$$

３次方程式では

$$
\begin{rcases}
{\small ① もともとの方程式の係数}\\
{\small ② 定数 \omega（３乗して 1 になる複素数）}\\
{\small ③ 整数など我々が普通に使っている数}\\
{\small ④ 差積 X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha) を添加}\\
{\small ⑤ ラグランジュ・リゾルベント A を添加}
\end{rcases}
\Rightarrow
{\small 解の公式が構成できた}
$$

　なお、 $${\sqrt{(X_5)^2}}$$ の代わりに $${X_5}$$

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

を $${Q(\omega)}$$ に添加しても構いません。その理由は
　$${\sqrt{(X_5)^2}=X_5, -X_5}$$
ですが、$${-X_5}$$ は $${-1}$$ と $${X_5}$$ の積で表現できるからです（注５）。よって、$${Q(\omega)}$$ に $${X_5}$$ を添加した集合 $${Q(\omega, X_5)}$$ は、集合として $${Q(\omega, \sqrt{(X_5)^2})}$$ と同じ、つまり
　$${Q(\omega, \sqrt{(X_5)^2})=Q(\omega, X_5)}$$
となります。拡大された $${Q(\omega, X_5)}$$ の世界では、新たに使える式（道具）として $${X_5}$$ が自由に使えることになります。
　このことを置換という観点で眺めてみます。

9. 『差積』の添加で対称性を遇置換シンメトリーまで絞り込む

　先ほどやったように、差積の２乗

$$
\begin{align*}
(X_5)^2=\{(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&\}^2
\end{align*}
$$

は５次置換で変化しない、つまり対称式でした。対称式なので $${\sqrt{(X_5)^2}}$$ は集合 $${Q(\omega)}$$ に含みます。一方差積

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

は遇置換でのみ対称性を保ちます。奇置換では $${-1}$$ 倍と変化するので対称式ではありません。

$$
\begin{align*}
&X_5 \xrightarrow[遇置換]{} X_5 \Rightarrow 変化しない\\
&X_5 \xrightarrow[奇置換]{} -X_5 \Rightarrow 変化する（-1 倍）
\end{align*}
$$

つまり $${\sqrt{(X_5)^2}}$$ の添加、ひいては $${X_5}$$ の添加によって、対称性を保つ置換は５次置換から遇置換まで絞られます。いわば対称性が「遇置換シンメトリー」にまで崩れているわけです。

$$
\begin{gather*}
５次置換\\[4pt]
\hspace{63pt}\downarrow \Leftarrow X_5 の添加\\[6pt]
遇置換
\end{gather*}
$$

そしてそれは、加減乗除で使える式の集合の拡大と対応しています。$${X_5}$$ の添加によって使える式を拡大すると、それに対応して対称性を保つ置換が遇置換にまで絞られます。添加によって集合を拡大すると、それに対応して対称性は崩れているわけです。

$$
\begin{gather*}
Q(\omega)\\
\hspace{66pt}\downarrow \Leftarrow X_5 の添加\\
Q(\omega, X_5)
\end{gather*}
\hspace{12pt}
\xleftrightarrow[対応]{}
\hspace{-40pt}
\begin{gather*}
５次置換\\
\hspace{63pt}\downarrow \Leftarrow X_5 の添加\\
遇置換
\end{gather*}
$$

３次方程式の解の公式の導出では、差積 $${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$ の添加から、さらにラグランジュ・リゾルベント $${A=\alpha+\omega\beta+\omega^2\gamma}$$ の添加によって、３次置換（$${6}$$ 通り）から遇置換（$${3}$$ 通り）、そして最終的に恒等置換（$${1}$$ 通り）にまで対称性を崩していくことができました。

$$
{\bf ３次置換}\\
\begin{align*}
&I\hspace{8pt}
(\alpha \beta \gamma)\hspace{8pt}
(\alpha \gamma \beta)\\
&(\beta \gamma)\hspace{8pt}
(\alpha \gamma)\hspace{8pt}
(\alpha \beta)
\end{align*}\\[4pt]
\hspace{66pt}\downarrow \Leftarrow X_3 の添加\\[6pt]
{\bf 遇置換}\\
\begin{align*}
&I\hspace{8pt}
(\alpha \beta \gamma)\hspace{8pt}
(\alpha \gamma \beta)
\end{align*}\\[4pt]
\hspace{63pt}\downarrow \Leftarrow A の添加\\[6pt]
{\bf 恒等置換}\\
I
$$

なお冒頭でもやりましたが、この対称性が崩れていく過程は使える式の拡大に対応しています。使える式の集合が大きくなるにつれて、対称性を保つ置換が崩れていきます。

$$
\begin{gather*}
Q(\omega)\\
\hspace{66pt}\downarrow \Leftarrow X_3 の添加\\
Q(\omega, X_3)\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
Q(\omega, X_3, A)
\end{gather*}
\hspace{15pt}
\xleftrightarrow[対応]{}
\hspace{-15pt}
\begin{gather*}
３次置換（対称式）\\
\hspace{66pt}\downarrow \Leftarrow X_3 の添加\\
遇置換\\
\hspace{63pt}\downarrow \Leftarrow A の添加\\
恒等置換
\end{gather*}
$$

差積 $${X_3}$$ の添加は平方根の利用を意味していました。また、ラグランジュ・リゾルベント $${A}$$ の添加は３乗根の利用を意味していました。そして最終的に恒等置換にまで対称性を崩すことによって、平方根、３乗根と累乗根を用いて解の式 $${\alpha, \beta, \gamma}$$ を構成することができ、解の公式が導出されたのです。
　５次置換においても、$${120}$$ 通りあった５次置換は差積 $${X_5}$$ の添加によって遇置換にまで対称性を崩し、$${60}$$ 通りまで絞り込むことができました。こまではうまくいっています。矛盾はおきていません。この後も適当な累乗根の添加によって遇置換からさらに対称性を崩していき、恒等置換にまで対称性を崩すことができれば解の公式は存在します。

$$
{\bf ５次置換}\\
120 通り\\[4pt]
\hspace{63pt}\downarrow \Leftarrow X_3 の添加\\[6pt]
{\bf 遇置換}\\
\hspace{4pt}60 通り\\[4pt]
\hspace{63pt}\downarrow \Leftarrow ？の添加\\[0pt]
\hspace{2pt}\vdots\\[4pt]
\hspace{63pt}\downarrow \Leftarrow ？の添加\\[6pt]
{\bf 恒等置換}
$$

しかし５次方程式の解の公式が存在しないことはわかっています。よって、この途中のどこかで矛盾が発生する。ではどこで矛盾が発生するのか、これがよくわかりません・・・」
　森田君はお手上げという表情で首を傾げた。
　どのように授業を誘導しようか少し考えた竹村は、ここは腕の見せ所と方向を見定めた。
「では森田君、同一の互換は連続何回作用すると元に戻るかな」
「２回です」
「そうだね。例えば恒置換でしか変化しないラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
について、互換 $${(\alpha \beta)}$$ を２回連続で作用させてみよう。$${\alpha}$$ と $${\beta}$$ の入れ替えを連続で行って

$$
\begin{gather*}
\alpha+\omega\beta+\omega^2\gamma\\
\hspace{74pt}\downarrow \Leftarrow (\alpha \beta) を作用\\
\beta+\omega\alpha+\omega^2\gamma\\
\hspace{74pt}\downarrow \Leftarrow (\alpha \beta) を作用\\
\alpha+\omega\beta+\omega^2\gamma
\end{gather*}
$$

より２回の作用で元に戻る。入れ替えた後、同じ入れ換えをもう一度行っているので変化しないのは当たり前だね。なお、互換は２次巡回置換とみることができる。同一の２次巡回置換は連続２回作用させると元に戻るということだね。では同一の３次巡回置換は連続何回作用すると元に戻るかな？」
「３回です」
「再びラグランジュ・リゾルベント
　$${A=\alpha+\omega\beta+\omega^2\gamma}$$
について、３次巡回置換 $${(\alpha \beta \gamma)}$$ を連続３回作用させてみよう。$${\alpha → \beta → \gamma → \alpha}$$ と巡回するので、$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\gamma}$$ に、$${\gamma}$$ を $${\alpha}$$ と巡回するように置き換えていって

$$
\begin{gather*}
\alpha+\omega\beta+\omega^2\gamma\\
\hspace{78pt}\downarrow \Leftarrow (\alpha \beta \gamma) を作用\\
\beta+\omega\gamma+\omega^2\alpha\\
\hspace{78pt}\downarrow \Leftarrow (\alpha \beta \gamma) を作用\\
\gamma+\omega\alpha+\omega^2\beta\\
\hspace{78pt}\downarrow \Leftarrow (\alpha \beta \gamma) を作用\\
\alpha+\omega\beta+\omega^2\gamma
\end{gather*}
$$

となり３回の作用で元に戻る。すると４次巡回置換は連続４回の操作で元に戻り、５次巡回置換は連続５回の操作で元に戻る。さらに先ほどやった $${n}$$ 次置換の定理Ⅰ

（定理Ⅰ）すべての $${n}$$ 次置換は、１つの互換、または複数の互換の積で表すことができる。

より、５次置換は１つの互換、または互換の積で表すことができる。それでここからが重要なんだけど・・・」
「あっ」
森田君は何かに気付いたように声を上げた。
「先生、できそうです！」
「えっ、できそう？」
「解の公式が存在しないことの証明は矛盾を導けばいいので・・・、そうか！次の授業までに考えていいですか！」

　今日の授業は終わった。
「森田君、何か気付いたのかな、何も教えていないけど・・・」
　なんとなく心が落ち着かない竹村は、おいしい梅割りでも飲もうと馴染みの小料理屋へと向かった。

（了）

（コメント）
推敲・校閲２回ほど行いましたが、一人でやるにはあまりにも大変なので、ほどほどにして投稿します（本文書くより大変）。書くか書かないか迷ったら書く方針でやっているので、必要以上に文面が長くなりがちです。時間をおいて後で読むといろいろと気付いてくるので、その都度修正していきます。訂正・不明な点があればコメント欄まで。
（追記）
投稿日が（８月２２日）が反映されない不具合？が発生しているかもしれません。もしかしたら一度誤って公開設定にしてしまったかも。複製して再アップも考えましたが、複製すると文字数が少なくなるという不具合も発生していて、リスクもあるのでこのまま様子をみます。

（注１）差積そのものを添加しても同じ集合になること

　$${\sqrt{(X_3)^2}}$$ を添加するのと、単に $${X_3}$$ を添加するのは同じになります。その理由は
　$${\sqrt{(X_3)^2}=\underline{X_3}, -X_3}$$
より、$${\sqrt{(X_3)^2}}$$ は $${X_3}$$ そのものか、それに $${-1}$$ を掛けた $${-X_3}$$ です。つまり、$${\sqrt{(X_3)^2}}$$ の添加によって自動的に $${X_3}$$（下線部）も添加されます。逆に $${X_3}$$ の添加によってそれに $${-1}$$ を掛ければ $${-X_3}$$ は構成できるので、 $${X_3}$$ を添加すれば $${\sqrt{(X_3)^2}}$$ を添加したことと同じになります。
　$${\sqrt{(X_3)^2}}$$ の添加 $${\longrightarrow}$$ $${X_3}$$ の添加
　$${X_3}$$ の添加 $${\longrightarrow}$$ $${-X_3}$$ は構成可能
$${\hspace{57pt}\longrightarrow}$$ $${\sqrt{(X_3)^2}}$$ の添加
すなわち
　「$${\sqrt{(X_3)^2}}$$ を添加するのと $${X_3}$$ を添加するのは同じ」
こととなり、$${Q(\omega, \sqrt{(X_3)^2})}$$ と、$${\sqrt{(X_3)^2}}$$ の代わりに $${X_3}$$ を添加した $${Q(\omega, X_3)}$$ は、集合として同じ範囲となります。
　$${Q(\omega, \sqrt{(X_3)^2})=Q(\omega, X_3)}$$

（注２）ラグランジュ・リゾルベントそのものを添加しも同じ集合になること

　$${\sqrt[3]{{A}^3}}$$ を添加するのと、単に $${A}$$ を添加するのは同じになります。その理由は
　$${\sqrt[3]{{A}^3}=\underline{A}, \omega A, \omega^2A}$$
より、$${\sqrt[3]{{A}^3}}$$ は $${A}$$ そのものか、それに $${\omega}$$ を掛けた $${\omega A}$$ または $${\omega^2A}$$ です。 $${\omega}$$ を１回掛ければ $${\omega A}$$、２回掛ければ $${\omega^2A}$$ です。集合 $${Q(\omega)}$$ にはあらかじめ $${\omega}$$ を加えてあるので、$${\omega}$$ は加減乗除の計算に自由に使えます。つまり、$${\sqrt[3]{{A}^3}}$$ の添加によって自動的に $${A}$$（下線部）も添加され、逆に $${A}$$ の添加によって $${\omega A}$$ と $${\omega^2A}$$ は構成できるので、 $${A}$$ を添加すれば $${\sqrt[3]{{A}^3}}$$ を添加したことと同じになります。
　$${\sqrt[3]{{A}^3}}$$ の添加 $${\longrightarrow}$$ $${A}$$ の添加
　$${A}$$ の添加 $${\longrightarrow}$$ $${\omega A}$$ と $${\omega^2A}$$ は構成可能
$${\hspace{53pt}\longrightarrow}$$ $${\sqrt[3]{{A}^3}}$$ の添加
すなわち
　「$${\sqrt[3]{{A}^3}}$$ を添加するのと $${A}$$ を添加するのは同じ」
こととなり、$${Q(\omega, \sqrt{(X_3)^2}, \sqrt[3]{{A}^3})}$$ と、$${\sqrt[3]{{A}^3}}$$ の代わりに $${A}$$ を添加した $${Q(\omega, \sqrt{(X_3)^2}, A)}$$ は集合として同じ範囲となります。

$$
\begin{align*}
Q(\omega, \sqrt{(X_3)^2}, \sqrt[3]{{A}^3})=Q(\omega, \sqrt{(X_3)^2}, A)
\end{align*}
$$

　なお（注１）より
　「$${\sqrt{(X_3)^2}}$$ を添加するのと $${X_3}$$ を添加するのは同じ」
なので、$${Q(\omega, \sqrt{(X_3)^2}, A)}$$ と $${Q(\omega, X_3, A)}$$ は集合として同じ範囲となります。

$$
\begin{align*}
Q(\omega, \sqrt{(X_3)^2}, A)=Q(\omega, X_3, A)
\end{align*}
$$

（注３）『背理法』について

　『背理法』とは、「ある命題の結論が正しいことを証明するために、その結論の否定を仮定して、すでに真であるとわかっている事実や元の命題の仮設などに矛盾することから、その命題の結論が正しいことを証明する方法」
　例えば次の命題を背理法で証明しましょう。
命題『ある整数 $${n}$$ について $${n^2}$$ が偶数であるとする。このとき $${n}$$ は偶数である。』
（証明）
　この命題の結論は「$${n}$$ は偶数である」。この結論の否定、つまり「$${n}$$ は奇数である」と仮定する（背理法の仮定）。$${n}$$ は奇数なので、$${k}$$ を $${0}$$ 以上の整数 ($${0, 1, 2, 3, \cdots}$$) として $${n=2k+1}$$ とおける *。
　ここで展開公式
　$${(a+b)^2=a^2+2ab+b^2}$$
を用いると

$$
\begin{align*}
n^2&=(2k+1)^2\\
&=(2k)^2+2\cdot2k\cdot1+1^2\\
&=4k^2+4k+1\\
&=2(2k^2+2k)+1\\
&=2l+1 （ただし l=2k^2+2k とおいた）
\end{align*}
$$

すると、$${k}$$ は $${0}$$ 以上の整数であることから、$${l(=2k^2+2k)}$$ も $${0}$$ 以上の整数となるので、 $${2l+1}$$ は奇数である*。これは $${n^2}$$ が偶数であるという条件（元の命題の仮設）に矛盾しているので、これによって背理法の仮定「$${n}$$ は奇数である」が正しくないこと、つまり「$${n}$$ は偶数である」ことが証明された。（証明終）

＊奇数 $${1, 3, 5, 7, \cdots}$$ は
　$${1=2\times0+1}$$
　$${3=2\times1+1}$$
　$${5=2\times2+1}$$
　$${7=2\times3+1}$$
$${\hspace{23pt}\vdots}$$
より、$${n=2k+1}$$（$${k}$$ は $${0}$$ 以上の整数）の形で書ける。

（注４）「条件Ⅰ」を厳密に

　本文で述べた $${X}$$ の「条件Ⅰ」の５次置換バージョン

$${\boldsymbol{X}}$$ の「条件Ⅰ」（５次置換バージョン）
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は５次置換で対称性が壊れているが、$${X^2}$$ では５次置換で対称性を保つ。』

について、厳密には $${2}$$ 乗のところを $${p}$$ 乗にして議論しなければなりません。次がその $${p}$$ 乗のバージョンです。

$${\boldsymbol{X}}$$ の「条件Ⅰ」（５次置換 $${p}$$ 乗バージョン）
　『$${X}$$ は対称式ではないが、$${X^p}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は５次置換で対称性が壊れているが、$${X^p}$$ では５次置換で対称性を保つ。ただし $${p}$$ は素数。』

本シリーズでは当たり前のように $${p=2}$$ として議論を進めていますが、実際はその値で決まっているわけではなく、「条件Ⅰ」を満たす $${X}$$ が存在するためには $${p=2}$$ であることを証明する必要があります。
　$${p=2}$$ を証明するための全体の流れは、
『$${X}$$ は対称式ではないが、$${X^p}$$ は対称式である。』
より $${X}$$ は対称式ではないので、ある５次置換で $${X}$$ が $${X'\,(\ne X)}$$ に変化したとすると、その $${X'}$$ は
　$${X'=\omega_p X}$$
ただし $${\omega_p}$$ は $${1}$$ の $${p}$$ 乗恨（つまり $${p}$$ 乗すると $${1}$$ になる数）と表すことができ、かつ５次置換は１つの互換、または互換の積で表せることから（定理Ⅰ）、同じ互換を２回作用させると元に戻るという性質により
　$${p=2}$$
と決定するという流れです（この証明を本文中に入れるかどうか検討中。やや難しく長くなるので（注４）にしました）。
　なお $${p}$$ は素数となります。その理由は（注４）の最後に述べます。
　さて本題である $${p=2}$$ となる証明を述べていきます。まずは本文でもやった $${n}$$次置換についての（定理Ⅰ）です。

（定理Ⅰ）すべての $${n}$$ 次置換は、１つの互換、または複数の互換の積で表すことができる。

　これは $${n=2, 3, 4, 5, \cdots}$$ と $${2}$$ 以上のすべての自然数について成り立ちます。例えば $${n=3}$$ のとき、つまり３次置換が１つの互換、または互換の積で表されることはすでにやりました。本文中に具体例を上げています（なお、互換の積の表し方は１通りではなく複数通りありうることに注意）。
　同じことは５次置換についても成り立ちます。５次置換が１つの互換、または複数の互換の積で表されるということは、５次置換は１回の、または複数回の互換の作用であるとみなすことができます。よって５次置換（より一般に $${n}$$ 次置換）は互換で表されることから、先ほどの「定理Ⅰ」（５次方程式バージョン）について、５次置換のところを互換に替えて、次のように表現することができます。

$${\boldsymbol{X}}$$ の「条件Ⅰ」（互換バージョン）
　『$${X}$$ は対称式ではないが、$${X^p}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は互換で対称性が壊れているが、$${X^p}$$ ではすべての互換で対称性を保つ。ただし $${p}$$ は素数。』

この「条件Ⅰ」を満たす式 $${X}$$ が存在したとします。すると、前半の条件『$${X}$$ は対称式ではない』より、$${X}$$ を変化させるための互換が少なくとも１つ存在することになります。その変化させる互換を $${(i j)}$$ とします。
　すると、後半の条件『$${X^p}$$ は対称式である』より、$${X^p}$$ に互換 $${(i j)}$$ を作用させても変化しないので
　$${(i j){X^p}=X^p　\cdots ①}$$
なお $${X^p}$$ に $${(i j)}$$ を作用させるということは、$${X^p}$$ の $${X}$$ の部分に $${(i j)}$$ を作用させるということです。$${p}$$ は定数なので作用させても変化しません。つまり、$${X^p}$$ に $${(i j)}$$ を作用させるということは $${X}$$ に $${(i j)}$$ を作用させたものを $${p}$$ 乗するということなので
　$${(i j)X^p=\underbrace{(i j)X\cdot(i j)X\cdots(i j)X}_{p 個の積}}$$
$${\hspace{50pt}=\{(i j){X}\}^p}$$
より
　$${(i j)X^p=\{(i j){X}\}^p　\cdots ②}$$
$${①=②}$$ より
　$${\{(i j){X}\}^p=X^p　\cdots ③}$$
また $${X}$$ を変化させる互換を $${(i j)}$$ としたので、$${X}$$ に互換 $${(i j)}$$ を作用させて $${X'(\ne X)}$$ に変化したとすると
　$${(i j)X=X' (\ne X)　\cdots ④}$$
$${④}$$ を $${③}$$ に代入して
　$${{(X’)}^p=X^p \cdots ⑤}$$
これを $${X'}$$ について解くと
　$${X'=\omega_p X \cdots ⑥}$$
ただし $${\omega_p}$$ は
　$${(\omega_p)^p=1}$$ かつ $${\omega_p\ne1}$$
を満たす定数です。つまり $${{\omega}_{p}}$$ は「$${p}$$ 乗して $${1}$$ になる数（つまり $${1}$$ の $${p}$$ 乗恨）のうち、$${1}$$ ではない数」となります。
　なお最初の $${\omega_p}$$ の条件 $${(\omega_p)^p=1}$$ は、$${⑥}$$ の両辺を $${p}$$ 乗した
　$${(X')^p=(\omega_p X)^p}$$
さらに指数法則 $${(ab)^r=a^rb^r}$$ より
　$${(X')^p=(\omega_p)^p X^p}$$
とした式において、$${⑤}$$ 式 $${{(X’)}^p=X^p}$$ が成り立つための条件です。
　また次の条件 $${\omega_p\ne1}$$ は、$${⑥}$$ 式 $${X'=\omega_p X}$$ において $${X'=X}$$ とならないための条件です。①より $${X\ne X'}$$ でした。

　ここは抽象的なので具体的な例をあげると
＜$${\boldsymbol{p=2}}$$ のとき＞
　$${⑤}$$ について $${p=2}$$ として
　$${{X’}^2=X^2}$$
これを $${X'}$$ について解くと
　$${X’=\pm X}$$
ただし④より $${X'\ne X}$$ であったので、プラスの方は却下されて
　$${X’=-X \cdots (*1)}$$
よって $${X'}$$ は、$${X}$$ の $${-1}$$ 倍と決定します。
　また $${\omega_p}$$ を用いると、$${⑤}$$ について $${p=2}$$ とした
　$${(X’)^2=X^2}$$
より、一旦 $${\omega_2}$$ を用いて $${X'}$$ について解くと
　$${X'=\omega_2X　\cdots (*2)}$$
ただし $${\omega_2}$$ は、「$${2}$$ 乗して $${1}$$ になる数（つまり $${1}$$ の平方根 $${1, -1}$$）のうち、$${1}$$ ではない数」なので
　$${\omega_2=-1}$$
これを $${(*2)}$$ に代入して
　$${X'=-X}$$
となり、これは $${(*1)}$$ と一致します。

＜$${\boldsymbol{p=3}}$$ のとき＞
　$${⑤}$$ について $${p=3}$$ として
　$${(X’)^3=X^3}$$
これを $${X'}$$ について解くと
　$${X’=X, \omega X, \omega^2X}$$
ただし④より $${X'\ne X}$$ であったので、$${X}$$ は却下されて
　$${X’=\omega X, \omega^2X \cdots (*3)}$$
なお $${\omega}$$ は、「３乗して１になる数（つまり１の３乗根）のうち、１ではない数」です。つまり
　$${\omega=\dfrac{1+\sqrt{3}i}{2}}$$　または　$${\dfrac{1-\sqrt{3}i}{2}}$$
を表す虚数の定数となります。
　また $${\omega_p}$$ を用いると、$${⑤}$$ について $${p=3}$$ とした
　$${(X’)^3=X^3}$$
より、一旦 $${\omega_3}$$ を用いて $${X'}$$ について解くと
　$${X'=\omega_3 X　\cdots (*4)}$$
ただし $${\omega_3}$$ は、「$${3}$$ 乗して $${1}$$ になる数（つまり $${1}$$ の $${3}$$ 乗恨 $${1, \omega, \omega^2}$$）のうち、$${1}$$ ではない数」なので
　$${\omega_3=\omega, \omega^2}$$
これを $${(*4)}$$ に代入して
　$${X’=\omega X, \omega^2X}$$
となり、これは $${(*3)}$$ と一致します。

　さらに、 $${④}$$ 式 $${(i j)X=X')}$$ を $${⑥}$$ 式 $${X'=\omega_p X}$$ に代入して
　$${(i j)X=\omega_p X \cdots ⑦}$$
この式は、$${X}$$ に互換 $${(i j)}$$ を作用させると「$${X}$$ は $${\omega_p(\ne1)}$$ 倍に変化する」ということを意味しています。$${X}$$ が全く違う式に変化するのではなく、$${X}$$ の $${\omega_p(\ne1)}$$ 倍という限定的な変化です。
　さて、ここから $${p}$$ を決定する作業に入ります。互換 $${(i j)}$$ は連続２回作用させると元に戻る、つまり恒等置換 $${I}$$ となるので
　$${(i j)(i j)=I}$$
すると、恒等置換 $${I}$$ は $${X}$$ に作用させても変わらないので
　$${X=IX}$$
より
　$${X=(i j)(i j)X \cdots ⑧}$$
右辺は $${X}$$ に $${(i j)}$$ を作用させてから、さらに同じ $${(i j)}$$ を作用させるということなので $${⑧}$$ は
　$${X=(i j)\{(i j)X\} \cdots ⑨}$$
と表せます。中カッコ $${\{\hspace{16pt}\}}$$ から先に計算していくという合図です。この中カッコに $${⑦}$$ を代入すると
　$${X=(i j)\{\omega_p X\}}$$
また $${(i j)}$$ が作用するのは $${X}$$ なので、$${(i j)}$$ を $${X}$$ の前に書いて
　$${X=\omega_p\{(i j)X\}}$$
再びこの中カッコ $${\{\hspace{16pt}\}}$$ に $${⑦}$$ を代入すると
　$${X=\omega_p\cdot\omega_p X}$$
より
　$${X=(\omega_p)^2 X}$$
この式が成り立つためには
　$${(\omega_p)^2=1 \cdots ⑩}$$
すると $${{\omega}_{p}}$$ は
　$${(\omega_p)^{\underline{p}}=1}$$ かつ $${\omega_p\ne1 \cdots ⑪}$$
を満たす定数だったので、これと $${⑩}$$ 式 $${(\omega_p)^{\underline{2}}=1}$$ との指数部分（下線部同士）の比較で $${p=2}$$ であることがわかり、$${⑪}$$ は
　$${(\omega_2)^2=1}$$ かつ $${\omega_2\ne1}$$
となります。よって $${\omega_2=1}$$ は却下されて
　$${\omega_2=-1}$$
と決定し、これを $${⑦}$$ 式 $${(i j)X=\omega_p X}$$ について $${p=2}$$ とした式
　$${(i j)X=\omega_2 X}$$
に代入すると
　$${(i j)X=-X \cdots ⑫}$$
また、$${①}$$ 式 $${(i j){X^p}=X^p}$$ について $${p=2}$$ とした式は
　$${(i j){X^2}=X^2 \cdots ⑬}$$
となります。
　以上より、$${⑫}$$ より $${X}$$ は互換 $${(i j)}$$ で（$${-1}$$ 倍に）変化し、かつ $${⑬}$$ より $${X^2}$$ は互換 $${(i j)}$$ で変化しないので、これで「条件１」（５次置換 $${p}$$ 乗バージョン）

$${\boldsymbol{X}}$$ の「条件Ⅰ」（５次置換 $${p}$$ 乗バージョン）　
『$${X}$$ は対称式ではないが、$${X^p}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は５次置換で対称性が壊れているが、$${X^p}$$ では５次置換で対称性を保つ。ただし $${p}$$ は素数。』

において、このような $${X}$$ が存在するためには、$${p=2}$$ とした場合

　$${\boldsymbol{X}}$$ の「条件Ⅰ」（$${p=2}$$ バージョン）
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は互換で対称性が壊れているが、$${X^2}$$ ではすべての互換で対称性を保つ。』

であることがわかりました。素数 $${p}$$ は $${3}$$ でも $${5}$$ でもなく $${p=2}$$ のみですよ、ということです。本シリーズでは $${p=2}$$ は証明無しで、それを前提として進めています。そしてその $${X}$$ として、２次方程式の解の公式の導出においては、２つの解の差積
　$${X_2=\alpha-\beta}$$
を取ればいいことがわかります。$${X_2}$$ は互換 $${(\alpha \beta)}$$ で $${-1}$$ 倍と変化し対称性が壊れていますが、$${X^2}$$ はすべての互換で対称性を保つ、つまり対称式です。

$$
\begin{align*}
(\alpha \beta)
\hspace{7pt}では\hspace{7pt}
\begin{cases}
\begin{align*}
X_2=\alpha-\beta \longrightarrow X'_2=& \beta-\alpha\\
=&-\alpha+\beta\\
=&-(\alpha-\beta)\\
=&\hspace{-8pt}\underbrace{-X}_{-1 倍に変化}\\[14pt]
\Rightarrow & {\small \boldsymbol{対称性が壊れている}}
\end{align*}\\[35pt]
\begin{align*}
(X_2)^2={(\alpha-\beta)}^2 \longrightarrow (X'_2)^2=& {(\beta-\alpha)}^2\\
=& (-\alpha+\beta)^2\\
=& \{-(\alpha-\beta)\}^2\\
=& \underbrace{{(\alpha-\beta)}^2}_{変化しない}\\[14pt]
\Rightarrow & {\small \boldsymbol{対称性を保つ}}
\end{align*}
\end{cases}
\end{align*}
$$

　すると３次方程式の解の公式の導出においては、「条件Ⅰ」を満たす解の式 $${X}$$ は３つの解の差積
　$${X_3=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
であり、４次方程式の解の公式の導出においては４つの解の差積、５次方程式の解の公式が存在しないことの証明においては、本文でやった５つの解の差積

$$
\begin{align*}
X_5=(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)&\\
\cdot\,(x_2-x_3)(x_2-x_4)(x_2-x_5)&\\
\cdot\,(x_3-x_4)(x_3-x_5)&\\
\cdot\,(x_4-x_5)&
\end{align*}
$$

となります。証明はいずれも２つの解の差積のときとまったく同様の議論になります。
　解がいくつあっても差積の２乗は必ず対称式になるので、その平方根である差積を添加して対称性を崩していくのは、方程式の次数に関わらず解の公式を導くための常套手段です。

（２次方程式の場合）

$$
\begin{align*}
&(\alpha-\beta)^2 は対称式\\
\Longrightarrow& 差積 \alpha-\beta を添加
\end{align*}
$$

（３次方程式の場合）

$$
\begin{align*}
&\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2 は対称式 \\ \Longrightarrow& 差積 (\alpha-\beta)(\beta-\gamma)(\gamma-\alpha) を添加
\end{align*}
$$

以下同様。（$${\Rightarrow}$$ 詳しくは本シリーズ (9)～）
　すると方程式の係数と差積の加減乗除で作られる式は遇置換で対称性を保ちます。次にその遇置換の対称性を、どのように崩していくのかが課題となります。最終的には恒等置換でのみ対称性を保つ式を作ることができれば解の公式の完成ですが、５次以上の方程式ではその遇置換の対称性を崩すことができない（よって５次以上の方程式には解の公式が存在しない）、というのがアーベルやガロアの証明した結論であり、本シリーズで解説していることとなります。

＜$${\boldsymbol{X^p}}$$ の $${\boldsymbol{p}}$$ が素数である理由＞
　最後に「条件Ⅰ」において、 $${X^p}$$ の $${p}$$ が素数である理由ですが、それは解の公式を導くにあたって、使える式を拡大していくための
　「$${X^p}$$ の $${p}$$ 乗恨 $${\sqrt[p]{X^p}}$$ の添加」
に由来します。つまり２次方程式では
　「$${X^2}$$ の $${2}$$ 乗恨（平方根） $${\sqrt{X^2}}$$ の添加」
３次方程式では
　「$${X^3}$$ の $${3}$$ 乗恨 $${\sqrt[3]{X^3}}$$ の添加」
が解の公式を導出するための常套手段です（なお
　$${\sqrt{(X_2)^2}}$$ の添加は $${X_2}$$ の添加と同じ
　$${\sqrt{(X_3)^2}}$$ の添加は $${X_3}$$ の添加と同じ
ことはすでにやりました（$${\Rightarrow}$$ 詳しくは本シリーズ (9)～(14)）。
　つまり $${p}$$ が素数でない場合、例えば $${p=4}$$ だとすると、そのときは $${X^4}$$ の $${4}$$ 乗恨 $${\sqrt[4]{X^4}}$$ の添加ではなく、$${4=2\times2}$$ より累乗根の法則 $${\sqrt[s\times t]{A}=\sqrt[s]{A}\cdot\sqrt[t]{A}}$$ を用いて
　$${\sqrt[4]{X^4}=\sqrt[2\times2]{X^4}=\sqrt[(2)]{X^4}\cdot\sqrt[(2)]{X^4}=\sqrt{X^4}\cdot\sqrt{X^4}}$$
（なお指数（左肩の数字）の $${2}$$ は省略する）
と計算できるので、より指数の小さい平方根 $${\sqrt{X^4}}$$ の添加で十分となります。
　例えば $${p=6}$$ だとすると、そのときは $${X^6}$$ の $${6}$$ 乗恨 $${\sqrt[6]{X^6}}$$ の添加ではなく、$${6=2\times3}$$ より
　$${\sqrt[6]{X^6}=\sqrt[2\times3]{X^6}=\sqrt[2]{X^6}\cdot\sqrt[3]{X^6}}$$
と計算できるので、より指数の小さい平方根 $${\sqrt[2]{X^6}}$$ と３乗恨 $${\sqrt[3]{X^6}}$$ の添加で十分となります。

（注５）差積そのものを添加しても同じ集合になること

　$${\sqrt{(X_5)^2}}$$ を添加するのと、単に $${X_5}$$ を添加するのは同じになります。これは（注１）で述べた、同じ差積である $${X_3}$$ のときと同じ理由になります。一応その理由を述べると
　$${\sqrt{(X_5)^2}=\underline{X_5}, -X_5}$$
より、$${\sqrt{(X_5)^2}}$$ は $${X_5}$$ そのものか、それに $${-1}$$ を掛けた $${-X_5}$$ です。つまり、$${\sqrt{(X_5)^2}}$$ の添加によって自動的に $${X_5}$$（下線部）も添加されます。逆に $${X_5}$$ の添加によってそれに $${-1}$$ を掛ければ $${-X_5}$$ は構成できるので、 $${X_5}$$ を添加すれば $${\sqrt{(X_5)^2}}$$ を添加したことと同じになります。
　$${\sqrt{(X_5)^2}}$$ の添加 $${\longrightarrow}$$ $${X_5}$$ の添加
　$${X_5}$$ の添加 $${\longrightarrow}$$ $${-X_5}$$ は構成可能
$${\hspace{57pt}\longrightarrow}$$ $${\sqrt{(X_5)^2}}$$ の添加
すなわち
　「$${\sqrt{(X_5)^2}}$$ を添加するのと $${X_5}$$ を添加するのは同じ」
こととなり、$${Q(\omega, \sqrt{(X_5)^2})}$$ と、$${\sqrt{(X_5)^2}}$$ の代わりに $${X_5}$$ を添加した $${Q(\omega, X_5)}$$ は、集合として同じ範囲となります。
　$${Q(\omega, \sqrt{(X_5)^2})=Q(\omega, X_5)}$$

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となることを解説
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除できる式の範囲を拡大。その結果、対称性を５次置換から遇置換（遇置換シンメトリー）へと絞り込む。

この記事が参加している募集

数学がすき

2,817件

この記事が気に入ったらサポートをしてみませんか？