ここでは、「体」という新しい概念と、本文で何度も述べてきた「累乗根の添加」について解説します。前半は、本シリーズ (18) の（注３）（注４）で述べた内容を、体を用いて新たに書き直したものです。
　後半では、具体的な２次方程式の解について、前半で述べた「体」と「累乗根の添加」を応用させていきます。

『体（たい）』について

　まずは有理数の集合を考えてみましょう（数の分類については（注１））。
　有理数とは、$${\dfrac{2}{3},   -\dfrac{5}{12}}$$ のように分数で表せる数です。$${5}$$ や $${0}$$ のような整数も、分数で表せるので有理数です。

　$${5=\dfrac{5}{1}}$$（有理数）

　$${0=\dfrac{0}{1}}$$（有理数）

　有理数の特徴として、「有理数同士で加減乗除を行っても有理数である」という性質があります。加減乗除とは、たし算・ひき算・かけ算・わり算のことです。
　有理数 $${+}$$ 有理数 $${=}$$ 有理数
　有理数 $${-}$$ 有理数 $${=}$$ 有理数
　有理数 $${\times}$$ 有理数 $${=}$$ 有理数
　有理数 $${\div}$$ 有理数 $${=}$$ 有理数

　具体例で確認してみます。２つの有理数 $${\dfrac{3}{2}}$$ と $${\dfrac{1}{5}}$$ について、加減乗除をそれぞれ計算してみると

　$${\dfrac{3}{2}+\dfrac{1}{5}=\dfrac{15}{10}+\dfrac{2}{10}=\dfrac{17}{10}}$$（有理数）

　$${\dfrac{3}{2}-\dfrac{1}{5}=\dfrac{15}{10}-\dfrac{2}{10}=\dfrac{13}{10}}$$（有理数）

　$${\dfrac{3}{2}\times\dfrac{1}{5}=\dfrac{3\times1}{2\times5}=\dfrac{3}{10}}$$（有理数）

　$${\dfrac{3}{2}\div\dfrac{1}{5}=\dfrac{3}{2}\times\dfrac{5}{1}=\dfrac{3\times5}{2\times1}=\dfrac{15}{2}}$$（有理数）

　このように、有理数同士で加減乗除を行っても有理数です。このことを「有理数の集合は加減乗除で閉じている」といいます。
　この、加減乗除で閉じた集合のことを『体（たい）』といいます。つまり、有理数の集合は体です。
　では、整数の集合は体でしょうか？整数 $${2}$$ と $${5}$$ で計算してみると
　$${2+5=10}$$（整数）
　$${2-5=-3}$$（整数）
　$${2\times5=10}$$（整数）
　$${2\div5=\dfrac{2}{5}=0.4}$$（整数ではない）
より、整数同士のわり算は常に整数とはならないので、加減乗除で閉じてはいません。つまり、整数の集合は体ではありません。

体の例

　有理数の集合は、加減乗除で閉じているので『有理数体』といい、記号 $${\mathbb{Q}}$$ で表します（有理数の英語名は rational number であるが、「R」は以下に述べる実数で使用しているので、割り算の商を意味するイタリア語名 Quoziente から「Q」を使用している）。
　また
　実数 $${+}$$ 実数 $${=}$$ 実数
　実数 $${-}$$ 実数 $${=}$$ 実数
　実数 $${\times}$$ 実数 $${=}$$ 実数
　実数 $${\div}$$ 実数 $${=}$$ 実数
より、実数の集合も、加減乗除で閉じているので『実数体』といい、記号 $${\mathbb{R}}$$ で表します（英語名 Real number の頭文字）。
　さらに
　複素数 $${+}$$ 複素数 $${=}$$ 複素数
　複素数 $${-}$$ 複素数 $${=}$$ 複素数
　複素数 $${\times}$$ 複素数 $${=}$$ 複素数
　複素数 $${\div}$$ 複素数 $${=}$$ 複素数
より、複素数の集合も、加減乗除で閉じているので『複素数体』といい、記号 $${\mathbb{C}}$$ で表します（英語名 Complex number の頭文字）。

　有理数体 $${\mathbb{Q}}$$・・・ 加減乗除で閉じている有理数の集合
　実数体 $${\mathbb{R}}$$　・・・ 加減乗除で閉じている実数の集合
　複素数体 $${\mathbb{C}}$$・・・ 加減乗除で閉じている複素数の集合

　ちなみに、この３つの体には次のような包含関係があります。
　$${\mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}}$$

「添加」について（復習）

　ここで、有理数体を $${\mathbb{Q}}$$ とします。この有理数体に、有理数ではない（無理数である） $${\sqrt{2}}$$ を添加し、拡大された体を $${\mathbb{Q}(\sqrt{2})}$$ とします。いわば旧種の数の集合である有理数体に、新種の数である $${\sqrt{2}}$$ を、加減乗除の”仲間”に加えるわけです。

　ここで、添加とは
　「加減乗除で閉じた集合の範囲を拡大すること」
を意味します。もともと加減乗除で閉じた有理数体があり、それに新しい数 $${\sqrt{2}}$$ を添加して得られる、有理数と $${\sqrt{2}}$$ の加減乗除で閉じた集合が $${\mathbb{Q}(\sqrt{2})}$$ となります。この集合のことを、拡大された体という意味で『拡大体』といいます。
　また、拡大する前の最初の体を『基礎体』といいます．つまり
　$${\mathbb{Q}}$$ は基礎体
　$${\mathbb{Q}(\sqrt{2})}$$ は拡大体
となります。

　すると、拡大体 $${\mathbb{Q}(\sqrt{2})}$$ に含まれるのは次のような数です。
　もともと $${\mathbb{Q}}$$ に含まれる数（つまり有理数）はそのまま $${\mathbb{Q}(\sqrt{2})}$$ に含まれます。
　$${2}$$（整数）
　$${-1}$$（整数）
　$${\dfrac{3}{2}}$$（有理数）
　$${-\dfrac{1}{4}}$$（有理数）

　また下記のように、有理数と $${\sqrt{2}}$$ の加減乗除で得られる数も $${\mathbb{Q}(\sqrt{2})}$$ に含まれます。
　$${1+\sqrt{2}}$$
　$${2-\sqrt{2}}$$
　$${-4+3\sqrt{2}}$$
　$${5\sqrt{2}\\[-15pt]}$$
　$${\dfrac{1}{3}-\dfrac{2}{5}\sqrt{2}\\[-12pt]}$$
　$${\dfrac{\sqrt{2}}{3}\\[-16pt]}$$
　$${\sqrt{2}}$$（添加した数そのもの）

　なお、$${\mathbb{Q}(\sqrt{2})}$$に含まれる式は、$${s,  t}$$ を有理数として
　$${s+t\sqrt{2}}$$
という形で書くことができます。上の例はすべてそのような形で表されています。
　例えば整数 $${2}$$ は、$${s=2,  t=0}$$ とすれば得られます。
　$${s+t\sqrt{2}=2+0\cdot\sqrt{2}=2}$$
　添加した $${\sqrt{2}}$$ そのものは、$${s=0,  t=1}$$ とすれば得られます。
　$${s+t\sqrt{2}=0+1\cdot\sqrt{2}=\sqrt{2}}$$
　もちろん $${2+3\sqrt{2}}$$ は、$${s=2,  t=3}$$ とすればOKです。
　$${s+t\sqrt{2}=2+3\cdot\sqrt{2}=2+3\sqrt{2}}$$

　では、$${2+3\sqrt{2}}$$ と $${5-\sqrt{2}}$$ について、その加減乗除をそれぞれ計算してみましょう。加減乗除で閉じているので、足しても引いても掛けても割っても、その結果は $${s,  t}$$ を有理数として
　$${s+t\sqrt{2}}$$
という形で表されるはずです。この形で書けなければ $${\mathbb{Q}(\sqrt{2})}$$ に含まれません。例えば、$${s+t\sqrt{3}}$$ や $${s+t\sqrt{2}+u\sqrt{3}}$$ のような形になると、それは $${\mathbb{Q}(\sqrt{2})}$$ には含まれなくなります。
　では、実際に計算してみると

$$
\begin{align*}
&\begin{align*}
(2+3\sqrt{2})+(5-\sqrt{2})&=2+3\sqrt{2}+5-\sqrt{2}\\
&=2+5+3\sqrt{2}-\sqrt{2}\\
&=7+(3-1)\sqrt{2}\\
&=7+2\sqrt{2}　（\mathbb{Q}(\sqrt{2}) に含まれる）
\end{align*}\\
&\begin{align*}
(2+3\sqrt{2})-(5-\sqrt{2})&=2+3\sqrt{2}-5+\sqrt{2}\\
&=2-5+3\sqrt{2}+\sqrt{2}\\
&=-3+(3+1)\sqrt{2}\\
&=-3+4\sqrt{2}　（\mathbb{Q}(\sqrt{2}) に含まれる）
\end{align*}\\
&\begin{align*}
(2+3\sqrt{2})(5-\sqrt{2})&=2\cdot5-2\cdot\sqrt{2}+3\sqrt{2}\cdot5-3\sqrt{2}\cdot\sqrt{2}\\
&=10-2\sqrt{2}+15\sqrt{2}-3\cdot(\sqrt{2})^2\\
&=10-2\sqrt{2}+15\sqrt{2}-3\cdot2（(\sqrt{2})^2=2 より）\\
&=10-2\sqrt{2}+15\sqrt{2}-6\\
&=10-6-2\sqrt{2}+15\sqrt{2}\\
&=4+(15-2)\sqrt{2}\\
&=4+13\sqrt{2}　（\mathbb{Q}(\sqrt{2}) に含まれる）
\end{align*}\\
&\begin{align*}
\dfrac{2+3\sqrt{2}}{5-\sqrt{2}}&=\dfrac{(2+3\sqrt{2})(5+\sqrt{2})}{(5-\sqrt{2})(5+\sqrt{2})}　（分母の有利化）\\
&=\dfrac{2\cdot5+2\cdot\sqrt{2}+3\sqrt{2}\cdot5+3\sqrt{2}\cdot\sqrt{2}}{5^2-(\sqrt{2})^2}　\cdots (*)\\
&=\dfrac{10+2\sqrt{2}+15\sqrt{2}+3(\sqrt{2})^2}{25-2}\\
&=\dfrac{10+2\sqrt{2}+15\sqrt{2}+3\cdot2}{23}\\
&=\dfrac{10+2\sqrt{2}+15\sqrt{2}+6}{23}\\
&=\dfrac{10+6+2\sqrt{2}+15\sqrt{2}}{23}\\
&=\dfrac{16+(2+15)\sqrt{2}}{23}\\
&=\dfrac{16+17\sqrt{2}}{23}\\
&=\dfrac{16}{23}+\dfrac{17}{23}\sqrt{2}　（\mathbb{Q}(\sqrt{2}) に含まれる）
\end{align*}
\end{align*}
$$

　よって、どれも $${s,  t}$$ を有理数として
　$${s+t\sqrt{2}}$$
の形で表されるので、集合 $${\mathbb{Q}(\sqrt{2})}$$ は加減乗除で閉じていることが分かります。今は１回の計算のみ確認しましたが、どのような複雑な計算でも、一つ一つの加減乗除の連続で計算されるので、最終的な結果はやはり $${s+t\sqrt{2}}$$ の形で表されます。
　なお $${(*)}$$ の分母では展開公式
　$${(a+b)(a-b)=a^2-b^2}$$
を利用しています。

２次方程式の解は、どの体に含まれるのか？

　ここで、２次方程式の解が、有理数体 $${\mathbb{Q}}$$ に含むか含まないかを考えてみましょう。まずは、２次方程式の解の公式を復習します。

＜２次方程式の解の公式＞

　２次方程式 $${ax^2+bx+c=0}$$ について

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

＊＊＊

　この解の公式を用いて、２次方程式 $${2x^2+x-3=0}$$ の解を求めてみます。すると、$${a=2,   b=1,   c=-3}$$ より

$$
\begin{align*}
x&=\dfrac{-1\pm\sqrt{1^2-4\times2\times(-3)}}{2\times2}\\
&=\dfrac{-1\pm\sqrt{1+24}}{4}\\
&=\dfrac{-1\pm\sqrt{25}}{4}\\
&=\dfrac{-1\pm5}{4}　(\because \sqrt{25}=\sqrt{5^2}=5  より)\\
&=\dfrac{-1+5}{4},   \dfrac{-1-5}{4}\\
&=\dfrac{4}{4},   \dfrac{-6}{4}\\
&=1,  -\dfrac{3}{2}
\end{align*}
$$

よって、解は有理数となります。つまり、この解は有理数体 $${\mathbb{Q}}$$ の中に含まれます。

　次に、$${3x^2-x-1=0}$$ の解を求めてみます。
　$${a=3,   b=-1,   c=-1}$$ より

$$
\begin{align*}
x&=\dfrac{-(-1)\pm\sqrt{(-1)^2-4\times3\times(-1)}}{2\times3}\\
&=\dfrac{1\pm\sqrt{1+12}}{6}\\
&=\dfrac{1\pm\sqrt{13}}{6}\\
&=\dfrac{1+\sqrt{13}}{6},    \dfrac{1-\sqrt{13}}{6}
\end{align*}
$$

　$${\sqrt{13}}$$ は無理数です。よって、$${\sqrt{13}}$$ を含むこの解
　$${\dfrac{1+\sqrt{13}}{6},    \dfrac{1-\sqrt{13}}{6}}$$
も無理数になります。つまり、有理数体 $${Q}$$ の中にこの解は含まれません。

　しかし、$${Q}$$ に $${\sqrt{13}}$$ を添加した拡大体 $${Q(\sqrt{13})}$$ を考えると、その中には解が含まれます。それぞれの解は
　$${\dfrac{1+\sqrt{13}}{6}=(1+\sqrt{13})\div6}$$
　$${\dfrac{1-\sqrt{13}}{6}=(1-\sqrt{13})\div6}$$
と、有理数と $${\sqrt{13}}$$ の加減乗除によって構成できるからです。
　このように、それまで用いることのできなかった新しい数を添加し、体を拡大することによって、その拡大体の中に方程式の解を含むようにすることができます。

　このようにして、２次方程式の解が存在することを、「平行恨の添加による体の拡大」と関係づけることができます。体をどこまで拡大すれば解が含まれるのかが、解の公式が存在するかどうかのカギとなります。

一般の２次方程式について

　ここで、一般の２次方程式 $${ax^2+bx+c=0}$$ を考えます。ただし簡単のため、係数の範囲は有理数とします。係数は複素数まで拡張できますが、有理数の範囲で理解出来れば、複素数まで拡張することは難しくありません。
　ここで、係数 $${a,  b,  c}$$ と有理数の加減乗除で閉じている体を考え、その体を $${Q_2}$$ とします。

　$${Q_2=\{係数  a,  b,  c  と有理数の加減乗除で閉じている体\}}$$

　例えば $${Q_2}$$ には、次のような式（や数）が含まれます
　$${3}$$
　$${\dfrac{5}{2}}$$
　$${a+b+c}$$
　$${a-3bc}$$
　$${\dfrac{c}{2a}}$$

　ただし、平方根や３乗根は、$${a,  b,  c}$$ と有理数の加減乗除で求めることはできないので、$${Q_2}$$ に含まれません。例えば
　$${1+\sqrt{2}}$$
　$${\sqrt{a}}$$
　$${\sqrt{b^2-4ac}}$$
　$${\sqrt[3]{abc}}$$
は $${Q_2}$$ の要素に含まれません。

　さて、一般の２次方程式 $${ax^2+bx+c=0}$$ の解は、体 $${Q_2}$$ に含まれるでしょうか。２次方程式の解の公式は

＜２次方程式の解の公式＞

　２次方程式 $${ax^2+bx+c=0}$$ について

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

＊＊＊

なので、平方根 $${\sqrt{b^2-4ac}}$$ は体 $${Q_2}$$ からはみ出していることになります。平方根は、係数 $${a,  b,  c}$$ と有理数の加減乗除では構成できません。つまり、２次方程式 $${ax^2+bx+c=0}$$ の解は、体 $${Q_2}$$ には含まれません。

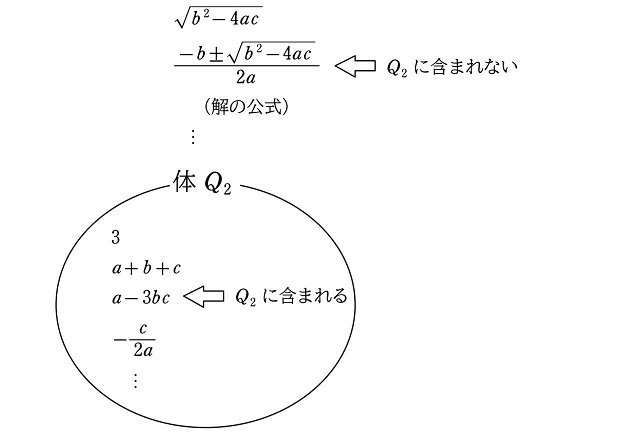
　そこで、この体 $${Q_2}$$ に $${\sqrt{b^2-4ac}}$$ を添加してみましょう。$${Q_2}$$ に $${\sqrt{b^2-4ac}}$$ を添加した体（拡大体）を $${Q_2(\sqrt{b^2-4ac})}$$ とします。つまり

　$${Q_2(\sqrt{b^2-4ac})=}$$ { 係数 $${a,  b,  c}$$ と有理数と $${\sqrt{b^2-4ac}}$$ の加減乗除で閉じた集合 }

　すると、この拡大体 $${Q_2(\sqrt{b^2-4ac})}$$ の中では、加減乗除のできる仲間として $${\sqrt{b^2-4ac}}$$ を含んでいるので、解の公式

$$
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

を

$$
\begin{align*}
x=(-1\times b\pm\sqrt{b^2-4ac}  )\div (2\times a)
\end{align*}
$$

と、加減乗除で構成することができます。

　つまり、解の公式が構成できること（解の公式が存在すること）と、それを構成できる拡大体が存在することの間に、対応関係を見出だすことができます。

$$
\begin{align*}
Q_2  &\underset{対応}{\longleftrightarrow}  x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}  を構成できない\\
&\hspace{-57pt}\bm{体の拡大}  \downarrow\\
Q_2(\sqrt{b^2-4ac})  &\underset{対応}{\longleftrightarrow}  x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}  を構成できる
\end{align*}
$$

　なお、添加する式としては $${\sqrt{b^2-4ac}}$$ だけに限られているわけではなく、都合のよい式を添加すればよいことになります。３次、４次、５次と高次の方程式にも応用させるためには、添加するものは、２次方程式の解 $${\alpha,  \beta}$$ の差積
　$${X_2=\alpha-\beta}$$
または、差積の２乗の平方根
　$${\sqrt{(X_2)^2}=\sqrt{(\alpha-\beta)^2}}$$
が採用されます（何次方程式でも解の差積は作れるので）（本シリーズ (21)）。

まとめ

　実は、アーベルの証明に出てきた「係数と有理数の加減乗除で構成される式の集合」は体のことです。拡大する前の最初の体なので、基礎体となります。係数による体なので、この基礎体を『係数体』と記しているテキストもあります。
　アーベルの証明でやったように、その方程式の「係数と有理数の加減乗除で構成される式の集合」（基礎体）では解の公式は構成できないので、平方根、３乗根と次々と累乗根を添加することによって、解の公式が存在するまで式の集合を拡大していくこと（拡大体を構成すること）が必要になります。
　例えば、３次方程式に解の公式が存在する理由は、大雑把にいえば、次のようなイメージです（本シリーズ (18) 他）。

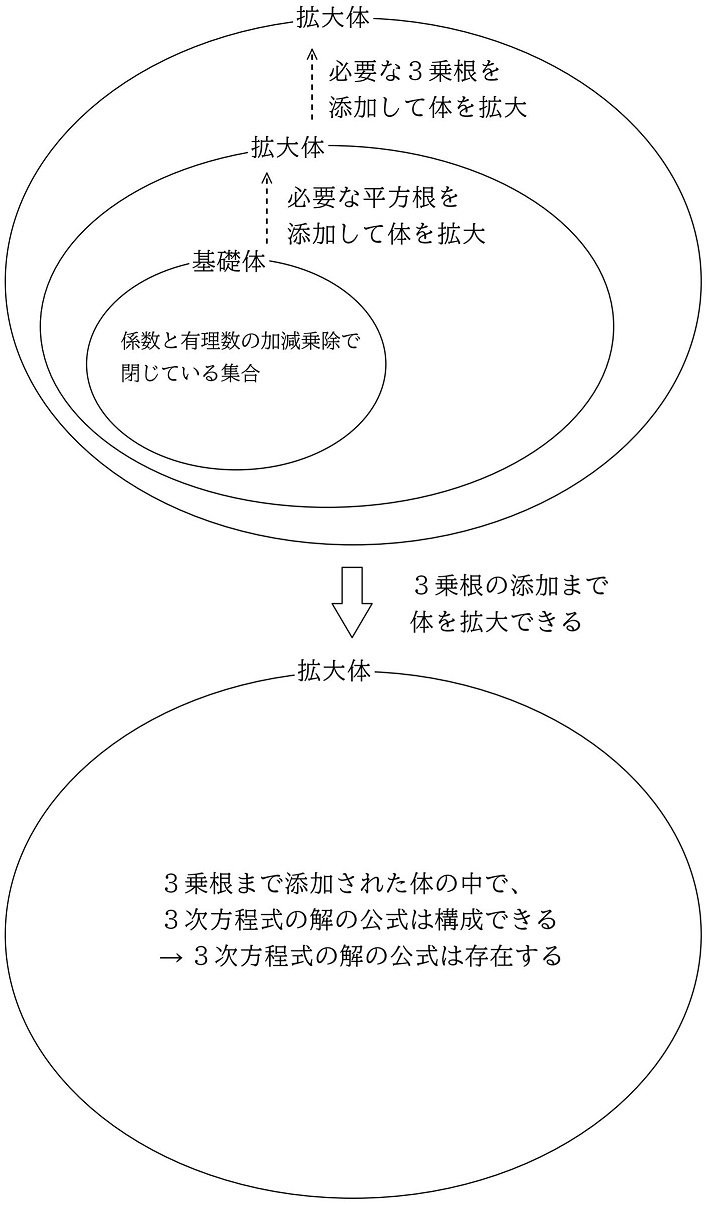
　また、５次方程式に解の公式が存在しない理由は、大雑把にいえば、次のようなイメージです（本シリーズ (18) 他）。

　しかし、解の公式が存在するかどうかの理論においては、ただ体を拡大するだけではなく、別の角度での理論立てが必要になります。それが、ガロアの発見した「群」という概念です。
　ガロアは、「正規部分群の縮小」と「体の拡大」には１対１の対応（ガロア対応）があることを見出し、５次以上の方程式には解の公式が存在しないことを証明しました。
　つまり、（その剰余群が巡回群になりながら）正規部分群を単位元のみの集合 $${\{id\}}$$ にまで縮小できれば、それと対応する拡大体の中で解の公式を構成することができる（解の公式が存在する）。しかし、単位元のみからなる集合 $${\{id\}}$$ まで縮小できなければ、解の公式を構成できる範囲まで体を拡大できないので解の公式が存在しない、というのがガロアの証明のアイデアです（本シリーズ (34)）。
　前置きが長くなりましたが、次からそれについて解説していきます。
　なお、アーベルの証明で書いた記事では、「対称性の破壊」が「正規部分群の縮小」に、「累乗根の添加」が「体の拡大」に対応しています。ガロアの証明では、群（の縮小）と体（の拡大）の対応関係が重要になります。

（コメント）

　前置きが長く、後から重要な概念が出てくるので、説明が冗長になった印象です。
　もともとアーベルの証明（のアイデアを現代風に表現したもの）を紹介する目的で書き始めたので、それ以降に発見されたガロアの「群」のアイデアを用いることができず、それにともない「体」の概念も用いないで証明を書いてきたので、説明がどうしても冗長になった印象です。
　（群は用いなくとも）最初の段階で「体」の概念をはっきりと導入すれば、もっと証明がすっきしたものになったかもしれません。書き直す機会があれば、構成をし直す必要があるかもしれません。

（注１）数の分類

　数の分類は以下の通りです。

$$
\begin{align*}
\boldsymbol{複素数  a+bi} 
\begin{cases}
\overset{\small b=0  のとき}{\boldsymbol{実数  a}}
\begin{cases}
\underset{\scriptsize 分数で表せる数}{\boldsymbol{有理数}}
\begin{cases}
\boldsymbol{整数}
\begin{cases}
\boldsymbol{自然数}  \scriptsize{(1,  2,  3, \cdots)}\\
\boldsymbol{0}\\
\boldsymbol{負の整数}  \scriptsize{(-1, -2, -3, \cdots)}
\end{cases}\\
\boldsymbol{有限小数}\\
　{\footnotesize 例　0.17 (=\dfrac{17}{100})}\\
\boldsymbol{循環小数{\scriptsize（循環する無限小数）}}\\
　{\footnotesize 例　0.232323\cdots\left(=\dfrac{23}{99}\right)}
\end{cases}\\
\underset{\scriptsize 分数で表せない数}{\boldsymbol{無理数}}\\
　{\scriptsize 例　\pi  (=3.1415\cdots)  のような \boldsymbol{循環しない無限小数}}\\
　　    {\scriptsize e  (=2.7182\cdots)  のような \boldsymbol{循環しない無限小数}}\\
\end{cases}\\
\overset{\small b\ne0  のとき}{\boldsymbol{虚数  a+bi}}　特に  a=0  のとき  \boldsymbol{bi}  を\boldsymbol{純虚数}という。 
\end{cases}
\end{align*}
$$

（参考）各章の内容

（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となること、及び「差積」と平方根を結ぶ等式の証明。
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式が存在するのか」を解説（添加する式について加筆予定）
（12）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（前編）。「差積の２乗の平方根」を用いて対称性を保つ置換を「遇置換」にまで絞り込む（対称性の破壊）。
（13）「アーベルの証明」のアイデアを用いて、なぜ「３次方程式の解の公式が存在するのか」を解説（後編）。「ラグランジュ・リゾルベント」を用いて対称性を保つ置換を「恒等置換」にまで絞り込む（対称性の破壊）。$${\longrightarrow}$$ ３次方程式の解の公式の完成
（14）「アーベルの証明」の解説①。５次方程式の解の差積（または差積の２乗の平方根）を添加して、加減乗除ができる式の範囲を拡大。その結果、構成可能な式の対称性が５次置換（対称式）から遇置換シンメトリーへと破壊されることを解説。
（15）「アーベルの証明」の解説②。すべての置換は互換で表せることから、５次置換をすべて互換の積で表して、遇置換と奇置換に分類する。
（16）「アーベルの証明」の解説➂。「すべての遇置換は３次巡回置換の積で表される」ことの解説。
（17）「アーベルの証明」の解説➃（最後）。「任意の３次巡回置換が５次巡回置換の積で表せる」ことによって、５次方程式には解の公式が存在しないことが証明されることの解説。
（18）もっと分かりやすくシリーズ①「累乗根の添加」について重点解説。
（19）もっと分かりやすくシリーズ②「対称性の破壊」について重点解説。
（20）もっと分かりやすくシリーズ③「対称性を恒等置換まで破壊」することについて重点解説。
（21）もっと分かりやすくシリーズ➃　何次方程式でも「最初に解の差積を添加して対称性を破壊すること」は常套手段。
（22）もっと分かりやすくシリーズ➄「解の和と差の連立」による２次方程式の解の公式の導出について。
（23）もっと分かりやすくシリーズ➅「対称式ではない解の公式を基本対称式で表す」ことのついて。
（24）もっと分かりやすくシリーズ➆「定数 $${\bm{\omega}}$$」について復習
（25）もっと分かりやすくシリーズ➇　３次方程式の解の公式の導出方法「カルダノの方法」を復習
（26）もっと分かりやすくシリーズ➈「カルダノの方法」と「対称性の破壊」の関連について
（27）もっと分かりやすくシリーズ⑩　そもそもなぜ解の公式が存在しないかを『巡回置換』から紐解く
（28）中学でも分かるガロアの証明①　ガロアの発見した「群」について簡単に解説
（29）中学でも分かるガロアの証明①　ガロアの発見した「部分群」について簡単に解説
（30）中学でも分かるガロアの証明③　ガロアの発見した「正規部分群」について
（31）中学でも分かるガロアの証明➃　正規部分群による剰余類の集合が群（剰余群）になること
（32）中学でも分かるガロアの証明⑤　単位元のみの正規部分群 $${\{𝑖𝑑\}}$$ による剰余類の集合が群（剰余群）になること
（33）中学でも分かるガロアの証明⑥　「巡回群」について、および剰余群が巡回群になること
（34）中学でも分かるガロアの証明⑦　２次対称群で、正規部分群による剰余群が巡回群になることの復習