（初めに）本記事はやや分かりにくいかもしれません（時間があれば修正します）。より分かりやすくは、本シリーズ (22)、(23) で全面的に書き直していますので、そちらもご参照ください。

（本文スタート）
　家庭教師の竹村が森田君の部屋に入ると、いつもと部屋の雰囲気が違うことに気付いた。
「あれ、部屋の壁変えた？」
「はい、この面を全部ホワイトボードにしました」
　壁一面が真っ白なホワイトボードになっている。そしてその真ん中に立つ小学５年生の森田君。
「先生、始めてよろしいでしょうか」
　さっそく”竹村ゼミ”が始まった。
「解の公式が存在する場合は式変形で具体的に導き出せば証明できますが、５次以上の方程式は解の公式が「存在しないこと」の証明なので、式変形ではない新しいアイデア、違う発想が必要になってきます。それが「解の置換」です。よって今後は解の置換という立場で解の公式を眺めていきます。なお解の置換という立場に立つと議論が抽象化していきますが、それは今までやった具体的な計算をもとにしているので、必要に応じてその計算にも触れていきます。
　まず２次方程式 $${ax^2+bx+c=0}$$ について考えます。この式について両辺を $${a}$$ で割って $${x^2}$$ の係数を $${1}$$ とします。

$$
\begin{align*}
&ax^2+bx+c=0\\
\leftrightarrows  &\dfrac{ax^2+bx+c}{a}=\dfrac{0}{a}\\
\leftrightarrows  &\dfrac{\bcancel{a}x^2}{\bcancel{a}}+\dfrac{bx}{a}+\dfrac{c}{a}=0\\
\leftrightarrows  &x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0
\end{align*}
$$

なお記号「$${\leftrightarrows}$$」は同値であることを意味します。例えば
　$${p\leftrightarrows q}$$
とは  $${p\hspace{-2pt}\underset{\tiny ならば}{\rightarrow}\hspace{-2pt}q}$$  とその逆  $${q\hspace{-2pt}\underset{\tiny ならば}{\rightarrow}\hspace{-2pt}p}$$  の両方が成り立つこと、つまり「$${p}$$ を仮定すると $${q}$$ が証明できる」、かつその逆「$${q}$$ を仮定すると $${p}$$ が証明できる」の両方が成り立つことを意味し、このとき $${p}$$ と $${q}$$ は同値であるといいます。

＜同値＞
　$${\underset{\tiny 仮定}{p}\hspace{-1pt}\rightarrow\hspace{-1pt}\underset{\tiny 結論}{q}}$$ とその逆 $${\underset{\tiny 仮定}{q}\hspace{-1pt}\rightarrow\hspace{-1pt}\underset{\tiny 結論}{p}}$$ の両方が成り立つとき、
　つまり $${p \leftrightarrows q}$$ が成り立つとき、$${p}$$ と $${q}$$ は同値であるという。
　$${p\rightarrow q}$$ は「$${p}$$ ならば $${q}$$」と読む。
　$${q\rightarrow p}$$ は「$${q}$$ ならば $${p}$$」と読む。

　すると、先ほどの変形

$$
\begin{align*}
&ax^2+bx+c=0\\
\leftrightarrows  &\dfrac{ax^2+bx+c}{a}=\dfrac{0}{a}\\
\leftrightarrows  &\dfrac{\bcancel{a}x^2}{\bcancel{a}}+\dfrac{bx}{a}+\dfrac{c}{a}=0\\
\leftrightarrows  &x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0
\end{align*}
$$

はどのステップも同値 $${\leftrightarrows}$$ である変形 、つまり同値変形になっているので、下から上に変形していくことも可能です。ここで簡単にするために

$$
\begin{align*}
\dfrac{b}{a}=a_1\\[7pt]
\dfrac{b}{a}=a_2
\end{align*}
$$

とおくと

$$
\begin{align*}
x^2+a_1x+a_2=0
\end{align*}
$$

この２次方程式の解を $${\alpha,  \beta}$$ とします。なお、２次方程式 $${ax^2+bx+c=0}$$ の解も、同じく $${\alpha,  \beta}$$ となることに注意しておきます。理由は $${x^2+a_1x+a_2=0}$$ と $${ax^2+bx+c=0}$$ は同値になるからです。

$$
\begin{align*}
x^2+a_1x+a_2=0 \leftrightarrows ax^2+bx+c=0
\end{align*}
$$

$${x^2+a_1x+a_2=0}$$ を仮定すると、 $${a_1=\dfrac{b}{a}}$$、$${a_2=\dfrac{c}{a}}$$ を代入してから両辺に $${a}$$ を掛けることによって $${ax^2+bx+c=0}$$ が証明でき、かつ $${ax^2+bx+c=0}$$ を仮定すると、 両辺を $${a}$$ で割ってから $${\dfrac{b}{a}=a_1}$$、$${\dfrac{b}{a}=a_2}$$ とおくと $${x^2+a_1x+a_2=0}$$ が証明できるので、$${x^2+a_1x+a_2=0}$$ と $${ax^2+bx+c=0}$$ は同値、つまり両者は同じ式となり、その解はどちらも同じ $${\alpha,  \beta}$$ となります。確認ですが

$$
\begin{align*}
&ax^2+bx+c=0\\
\leftrightarrows  &\dfrac{ax^2+bx+c}{a}=\dfrac{0}{a}\\
\leftrightarrows  &\dfrac{\bcancel{a}x^2}{\bcancel{a}}+\dfrac{bx}{a}+\dfrac{c}{a}=0\\
\leftrightarrows  &x^2+\dfrac{b}{a}x+\dfrac{c}{a}=0\\
\leftrightarrows  &x^2+a_1x+a_2=0
\end{align*}
$$

上の同値変形で、一番上の $${ax^2+bx+c=0}$$ と１番下の  $${x^2+a_1x+a_2=0}$$ は同値になるので、両者の解は同じです。すると解と係数の関係

＜解と係数の関係（復習）＞
　２次方程式 $${ax^2+bx+c=0}$$ の解を $${\alpha,  \beta}$$ とすると

$$
\begin{align*}
\alpha+\beta&=-\dfrac{b}{a}\\
\alpha\beta&=\dfrac{c}{a}
\end{align*}
$$

について、$${x^2+a_1x+a_2=0}$$ の解も $${\alpha,  \beta}$$ なので、 $${x^2+a_1x+a_2=0}$$ に解と係数の関係を適用させると $${a=1,  b=a_1,  c=a_2}$$ より

$$
\begin{align*}
\alpha+\beta&=-\dfrac{a_1}{1}\\
&=-a_1\\
\alpha\beta&=\dfrac{a_2}{1}\\
&=a_2
\end{align*}
$$

より

$$
\begin{align*}
\alpha+\beta&=-a_1\\
\alpha\beta&=a_2
\end{align*}
\hspace{5pt}\cdots (*1)
$$

よって、$${a_1,  a_2}$$ は

$$
\begin{align*}
a_1&=-(\alpha+\beta)\\
a_2&=\alpha\beta
\end{align*}
$$

するとここで注目したいのは、２次方程式 $${x^2+a_1x+a_2=0}$$ の係数 $${a_1}$$ と $${a_2}$$ は、２変数の基本対称式で表せるといういうことです。

$$
\begin{align*}
a_1&=-(\hspace{-5pt}\underbrace{\alpha+\beta}_{基本対称式}\hspace{-5pt})\\
a_2&=\underbrace{\alpha\beta}_{基本対称式}
\end{align*}
$$

これが、あらかじめ $${ax^2+bx+c=0}$$ の両辺を $${a}$$ で割って、$${x^2}$$ の係数を $${1}$$ にしつつ  $${\dfrac{b}{a}=a_1}$$、$${\dfrac{c}{a}=a_2}$$ と置いたことの効果です。係数 $${a_1,  a_2}$$ がダイレクトに基本対称式になります。解の公式を導くだけならこのような置き換えをする必要は特にありませんが、これから解説をする上で分かりやすくなります。
　すると、$${x^2+a_1x+a_2=0}$$ の係数 $${a_1}$$ と $${a_2}$$ は基本対称式そのものなので、$${a_1,  a_2}$$ の加減乗除で表される式は必ず対称式となります。例えば下記のような式は $${\alpha}$$ と $${\beta}$$ を入れ替えても式は変わらないので対称式です。

$$
\begin{align*}
2a_1+a_2&=2(\alpha+\beta)+\alpha\beta & &\rightarrow 対称式\\
3a_1\cdot a_2&=3(\alpha+\beta)\alpha\beta & &\rightarrow 対称式\\
\dfrac{{a_1}^2+4}{5a_2}
&=\dfrac{(\alpha+\beta)^2+4}{5\alpha\beta} & &\rightarrow 対称式
\end{align*}
$$

なお $${2}$$ や $${4}$$ のような、我々が知っている普通に使っている数は加減乗除に用いてもかまいません。対称性は基本対称式 $${\alpha+\beta}$$ と$${\alpha\beta}$$ の部分に依存し、その部分は $${\alpha}$$ と $${\beta}$$ を入れ替えても式は変わりません。よって $${\alpha+\beta}$$ と$${\alpha\beta}$$ を基本パーツとして、それと数との加減乗除で式を構成しても、その式の対称性は保たれるからです。逆に

$$
\begin{align*}
\boldsymbol{対称式は基本対称式の加減乗除で表すことができる}
\end{align*}
$$

という対称式の基本定理より、すべての対称式は基本対称式$${\alpha+\beta}$$ と$${\alpha\beta}$$ の加減乗除で表すことができ、さらに基本対称式は、すでに計算した解と係数の関係 $${(*1)}$$

$$
\begin{align*}
\alpha+\beta&=-a_1\\
\alpha\beta&=a_2
\end{align*}
\hspace{5pt}\cdots (*1)
$$

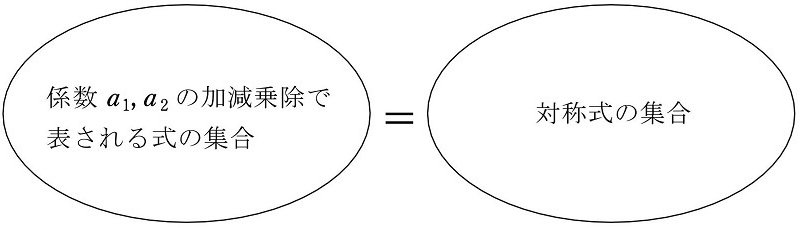
より $${a_1,  a_2}$$ の加減乗除を用いて表すことができます。つまり $${a_1,  a_2}$$ の加減乗除で表せる式の集まりと、対称式の集まりは等しくなります」
「その集まりのことを、数学的には『集合』という言葉を使うよ」
　竹村は補足を加えた。すると森田君は
「$${a_1,  a_2}$$ の加減乗除で表せる式の集合と、対称式を集めた集合は等しくなる、ということですね」と言いながら壁のホワイトボードに図を書き始めた。

　森田君は話を進める。
「また、当然のことながら $${\alpha-\beta}$$ や、解そのものを表す$${\alpha}$$、$${\beta}$$ のような式は対称式ではないので、$${a_1,  a_2}$$ の加減乗除で表すことはできません。例えば、解そのものを表す式 $${\alpha}$$ と $${\beta}$$ に、２次置換

$$
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
\hspace{10pt}と\hspace{10pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha\
\end{pmatrix}
$$

を作用させてみます。なお、復習として２次置換とは次のようなものでした。

＜$${\boldsymbol{\alpha}}$$ と $${\boldsymbol{\beta}}$$ の２次置換（復習）＞
➀　$${\alpha}$$ を $${\alpha}$$ に、$${\beta}$$ を $${\beta}$$ にと、そのままで変わらない置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow \alpha\\
\beta\longrightarrow \beta
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
$$

と表す。何も変わらない場合も置換に含める。これは「恒に等しい置換」という意味で『恒等置換』という。

②　$${\alpha}$$ を $${\beta}$$ に、$${\beta}$$ を $${\alpha}$$ に入れ替える置換、すなわち

$$
\begin{align*}
\alpha\longrightarrow \beta\\
\beta\longrightarrow \alpha
\end{align*}
\hspace{12pt}を\hspace{10pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha\
\end{pmatrix}
$$

と表す。（　　）の中の文字は、上から下へ置換されると考えればよい。

　すると $${\alpha}$$ と $${\beta}$$ は恒等置換 $${\dbinom{\alpha       \beta}{\alpha       \beta}}$$ では変化しませんが、$${\dbinom{\alpha       \beta}{\beta       \alpha}}$$ では $${\alpha}$$ が $${\beta}$$ に、$${\beta}$$ が $${\alpha}$$ に変化します。つまり $${\alpha,  \beta}$$ は対称式ではありません。

$$
\begin{align*}
&\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
\hspace{8pt}
では
\hspace{12pt}
\begin{cases}
\alpha \longrightarrow \alpha\\
\beta \longrightarrow \beta
\end{cases}
\hspace{4pt}\Rightarrow \boldsymbol{\small 変化しない}\\
&\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha
\end{pmatrix}
\hspace{8pt}
では
\hspace{12pt}
\begin{cases}
\alpha \longrightarrow \beta\\
\beta \longrightarrow\alpha
\end{cases}
\hspace{4pt}\Rightarrow \boldsymbol{\small 変化する（入れ替わる）}
\end{align*}
$$

式 $${\alpha}$$ と $${\beta}$$ を変化させないのは恒等置換のみとなります。すると解の公式とは、解をその方程式の係数で表すこと。つまり  $${x^2+a_1x+a_2=0}$$ の解を $${\alpha,  \beta}$$ としたとき

$$
\begin{align*}
\alpha=（係数  a_1  と  a_2  で表す）\\
\beta=（係数  a_1  と  a_2  で表す）
\end{align*}
$$

とすることですが、そもそも係数 $${a_1}$$ と $${a_2}$$ の加減乗除で表された式は対称式なので、左辺は対称式です。しかし右辺 $${\alpha,  \beta}$$ は対称式ではありません。

$$
\begin{align*}
\underbrace{\alpha}_{対称式でない}\hspace{-14pt}
=\underbrace{（係数  a_1  と  a_2  で表す）}_{加減乗除では対称式}\\
\underbrace{\beta}_{対称式でない}\hspace{-14pt}
=\underbrace{（係数  a_1  と  a_2  で表す）}_{加減乗除では対称式}
\end{align*}
$$

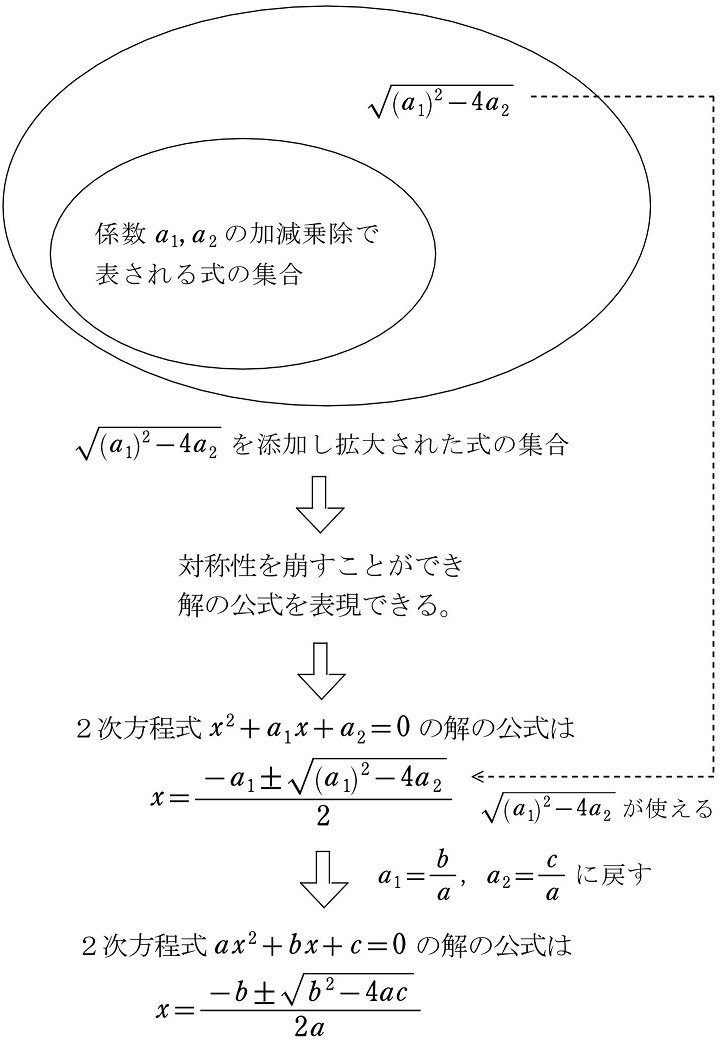
解の公式を導くには、基本対称式である $${a_1,  a_2}$$ を用いて表しつつも、最後に対称性を保つ置換を２次置換から恒等置換にまで崩し、$${\alpha,  \beta}$$ と同等の対称性、つまり恒等置換でしか変化しない式を作り上げる必要があります。一見矛盾したようにも思える課題。それを克服するアイデアが「累乗根の添加」というアイデアです。具体的には、 $${a_1,  a_2}$$ の加減乗除で得られる従来の式の「累乗根」の添加です。累乗根とは平方根、３乗根、４乗恨 $${\cdots}$$ のことです。
　なお累乗根は、$${a_1,  a_2}$$ の加減乗除で表すことはできません。よって、加減乗除できる対象として累乗根を新たに添加する必要があります。累乗根を新たに添加することによって、使える数体系を拡大、使える数の集合を大きくします。２次方程式では平方根 $${\sqrt{\hspace{15pt}}}$$ を添加しました。（⇒ 詳しくは本シリーズ (5)）
　３次方程式ではまずは平方根 $${\sqrt{\hspace{15pt}}}$$ を添加し、その平方根を用いてさらに３乗根 $${\sqrt[3]{\cdots\sqrt{\hspace{15pt}}}}$$ を添加しました。（⇒ 詳しくは本シリーズ (7)、(10)）
　累乗根を加減乗除のできる対象に加えることによって、対称性の壊れた式をつくることができる。累乗根を添加した拡大された数体系では、対称性のない $${\alpha,  \beta}$$ という式でも、その値を計算できるようになるのです。

　ではまず簡単に、２次方程式ではどう考えるのかを具体的に見ていきます。２次方程式では次のような条件を満たす「解の式」 $${X}$$ を考えます。

条件
　『$${X}$$ は対称式ではないが、$${X^2}$$ は対称式である。』
詳しく言うと
　『$${X}$$ は２次置換 $${\dbinom{\alpha       \beta}{\alpha       \beta},  \dbinom{\alpha       \beta}{\beta       \alpha}}$$ で対称性がこわれているが、$${X^2}$$ では２次置換で対称性を保つ。』

２次方程式の場合、そういう $${X}$$ は差積

$$
\begin{align*}
X=\alpha-\beta
\end{align*}
$$

でした。$${X=\alpha-\beta}$$ は恒等置換 $${\dbinom{\alpha       \beta}{\alpha       \beta}}$$ で変化しませんが、$${\dbinom{\alpha       \beta}{\beta       \alpha}}$$ では $${-1}$$ 倍に変化するので対称式ではありません。つまり２次置換で対称性がこわれています。しかし $${X^2=(\alpha-\beta)^2}$$ は恒等置換 $${\dbinom{\alpha       \beta}{\alpha       \beta}}$$ はもとより $${\dbinom{\alpha       \beta}{\beta       \alpha}}$$ でも変化しないので、$${X^2}$$ は対称式。つまり２次置換で対称性を保っています。

$$
\begin{align*}
\dbinom{\alpha       \beta}{\beta       \alpha}
\hspace{7pt}では\hspace{7pt}
\begin{cases}
\begin{align*}
\alpha-\beta \longrightarrow &  \beta-\alpha\\
=&-\alpha+\beta\\
=&\underbrace{-(\alpha-\beta)}_{-1  倍に変化}\\[15pt]
\Rightarrow &  {\small \boldsymbol{対称性が壊れている}}
\end{align*}\\[35pt]
\begin{align*}
{(\alpha-\beta)}^2 \longrightarrow &  {(\beta-\alpha)}^2\\
=&  (-\alpha+\beta)^2\\
=&  \{-(\alpha-\beta)\}^2\\
=&  \underbrace{{(\alpha-\beta)}^2}_{変化しない}\\[15pt]
\Rightarrow &  {\small \boldsymbol{対称性が保たれている}}
\end{align*}
\end{cases}
\end{align*}
$$

すると $${X^2=(\alpha-\beta)^2}$$ は、$${x^2+a_1x+a_2=0}$$ の解を $${\alpha,  \beta}$$ としたときの解と係数の関係 $${(*1)}$$

$$
\begin{align*}
\alpha+\beta&=-a_1\\
\alpha\beta&=a_2
\end{align*}
\hspace{5pt}\cdots (*1)
$$

から

$$
\begin{align*}
X^2&={(\alpha-\beta)}^2\\
&=\alpha^2-2\alpha\beta+\beta^2\\
&=\underline{\alpha^2+\beta^2}-2\alpha\beta\\
&=\underline{{(\alpha+\beta)}^2-2\alpha\beta}-2\alpha\beta\\
&={(\alpha+\beta)}^2-4\alpha\beta\\
&={(-a_1)}^2-4a_2\\
&={(a_1)}^2-4a_2
\end{align*}
$$

より

$$
\begin{align*}
X^2={(a_1)}^2-4a_2
\end{align*}
$$

下線部のところは
　$${\alpha^2+\beta^2={(\alpha+\beta)}^2-2\alpha\beta}$$
の恒等式を用いています。証明は右辺を展開して整理すると左辺になります。以下のように $${{(\alpha+\beta)}^2}$$ の展開公式と下線部が同値になることを用いてもいいでしょう。

$$
\begin{align*}
{(\alpha+\beta)}^2=\alpha^2+2\alpha\beta+\beta^2
\leftrightarrows \underline{\alpha^2+\beta^2={(\alpha+\beta)}^2-2\alpha\beta}
\end{align*}
$$

ここで簡単のため $${{(a_1)}^2-4a_2=A}$$ とおくと、$${X^2=A}$$ より 

$$
\begin{align*}
X=\pm\sqrt{A}
\end{align*}
$$

$${A={(a_1)}^2-4a_2}$$ だったので、ここで戻して

$$
\begin{align*}
X=\pm\sqrt{{(a_1)}^2-4a_2}
\end{align*}
$$

さらに $${X=\alpha-\beta}$$ より

$$
\begin{align*}
\alpha-\beta=\pm\sqrt{{(a_1)}^2-4a_2}
\end{align*}
$$

すると、解と係数の関係から得られる $${\alpha+\beta=-a_1}$$ と、先ほど求めた $${\alpha-\beta}$$ との連立方程式

$$
\begin{align*}
\begin{cases}
\alpha+\beta=-a_1\\
\alpha-\beta=\pm\sqrt{{(a_1)}^2-4a_2}
\end{cases}
\end{align*}
$$

を解くことによって $${\alpha,  \beta}$$ が決定できます。$${{(a_1)}^2-4a_2}$$ の平方根

$$
\begin{align*}
\sqrt{{(a_1)}^2-4a_2}
\end{align*}
$$

を加減乗除の対象として添加することによって解の公式が導出できるようになったのです。この連立方程式を解くには、$${\alpha+\beta}$$ と $${\alpha-\beta}$$ の和と差を２で割ることによって得られる $${\alpha,  \beta}$$ の恒等式

$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}
\end{align*}
$$

に、先ほど求めた $${\alpha+\beta}$$ と $${\alpha-\beta}$$ を代入します。（⇒ 詳しくは本シリーズ (5)）
　簡単に復習しますと $${\alpha-\beta}$$ にはプラスとマイナスの２通りがあるので、プラスのとき (case1) とマイナスのとき (case2) で場合分けをして

(case1)

$$
\begin{align*}
\begin{cases}
\alpha+\beta=\dfrac{b}{a}\\[10pt]
\alpha-\beta=\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{cases}
\end{align*}
$$

のとき

$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
&=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}\\
&=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

より

$$
\begin{align*}
\alpha=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
\beta=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

(case2)

$$
\begin{align*}
\begin{cases}
\alpha+\beta&=-\dfrac{b}{a}\\[10pt]
\alpha-\beta&=-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{cases}
\end{align*}
$$

のとき

$$
\begin{align*}
\alpha&=\dfrac{(\alpha+\beta)+(\alpha-\beta)}{2}\\
&=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
\beta&=\dfrac{(\alpha+\beta)-(\alpha-\beta)}{2}\\
&=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

より

$$
\begin{align*}
\alpha=\dfrac{-\dfrac{b}{a}-\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
\beta=\dfrac{-\dfrac{b}{a}+\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

(case1)、(case2) の結果を見ると、$${\alpha,  \beta}$$ の違いはプラスとマイナスの違いだけで $${\alpha,  \beta}$$ は対等で区別がないので、この式を一つにまとめることによって、$${x^2+a_1x+a_2=0}$$ の解の公式

$$
\begin{align*}
x=\dfrac{-a_1\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}
\end{align*}
$$

が得られるという構想になっています。さらに、これを以下のように計算していけば、教科書でも見慣れた２次方程式 $${ax^2+bx+c=0}$$ の解の公式が導かれます。

$$
\begin{align*}
x&=\dfrac{-\dfrac{b}{a}\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2}{a^2}-4\cdot\dfrac{c}{a}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2}{a^2}-4\cdot\dfrac{ac}{a^2}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2}{a^2}-\dfrac{4ac}{a^2}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\sqrt{\dfrac{b^2-4ac}{a^2}}}{2}\\
&=\dfrac{-\dfrac{b}{a}\pm\dfrac{\sqrt{b^2-4ac}}{a}}{2}\\
&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
$$

「図式化してみましょう」と、森田君は巨大な”壁”ホワイトボードを大きく使って図を書き始めた。ホワイトボードをすでに自在に操っている。

（図解）

ここでプラスの方を $${\alpha}$$、マイナスの方を $${\beta}$$ とおくと

$$
\begin{align*}
\alpha&=\dfrac{-b+\sqrt{b^2-4bc}}{2a}\\
\beta&=\dfrac{-b-\sqrt{b^2-4bc}}{2a}
\end{align*}
$$

となりますが、先に述べた $${\alpha,  \beta}$$ の２次置換

$$
\begin{pmatrix}
\alpha & \beta\\
\alpha & \beta
\end{pmatrix}
\hspace{10pt}と\hspace{10pt}
\begin{pmatrix}
\alpha & \beta\\
\beta & \alpha\
\end{pmatrix}
$$

において、恒等置換 $${\dbinom{\alpha       \beta}{\alpha       \beta}}$$ では $${\alpha}$$ は $${\alpha}$$ のまま、$${\beta}$$ は $${\beta}$$ のままで変化しませんが、 $${\dbinom{\alpha       \beta}{\beta       \alpha}}$$ では $${\alpha}$$ と $${\beta}$$ が入れ替わります。その入れ替えが、平方根ととったことに由来するプラスマイナスの入れ替えに対応していることになります。

$$
\begin{align*}
&\alpha=\dfrac{-b+\sqrt{b^2-4bc}}{2a}\\
\boldsymbol{\small 解の入れ替え}\hspace{2pt}&\hspace{-1pt}\updownarrow\hspace{30pt}\updownarrow\boldsymbol{\small \pm  の入れ替え}\\
&\beta=\dfrac{-b-\sqrt{b^2-4bc}}{2a}
\end{align*}
$$

つまり、そもそも対称式ではない $${\alpha}$$ と $${\beta}$$ を対称式で表すには、$${(\alpha-\beta)^2}$$ の平方根を取ることによって生じる $${\pm}$$ を利用することによって、対称式で表しつつもその対称性を $${\alpha,  \beta}$$ と同じレベルまで、すなわち $${\alpha}$$ と $${\beta}$$ の交換がプラスとマイナスの交換と一対一に対応するレベルにまで対称性を崩します。それによって、本来基本対称式の加減乗除だけで表すことは不可能な  $${\alpha,  \beta}$$ という対称性の無い式を、対称式で表すことが可能となったわけです」
「なるほど。すると、２次方程式の解の公式が存在するかどうかは、先に述べた条件

条件
　『$${X}$$ は２次置換 $${\dbinom{\alpha       \beta}{\alpha       \beta},  \dbinom{\alpha       \beta}{\beta       \alpha}}$$ で対称性がこわれているが、$${X^2}$$ では２次置換で対称性を保つ。』

を満たす $${X}$$ が存在するかどうか、これにつきるということだね」
「そうです。この条件を満たす $${X}$$ が存在すれば２次方程式の解の公式が存在する。この条件を満たす $${X}$$ が存在しなければ、２次方程式の解の公式は存在しないわけです。すると２次方程式の場合、その $${X}$$ は２つの解の差
　$${X=\alpha-\beta}$$
でした。そしてそれは対称式である
　$${X^2=(\alpha-\beta)^2}$$
の平方根を取って

$$
\begin{align*}
X&=\alpha-\beta\\
&=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{align*}
$$

と $${\alpha-\beta}$$ を具体的に決定できたからこそ、これと $${\alpha+\beta=-\dfrac{b}{a}}$$ との連立によって２次方程式の解の公式を導くことに成功したわけです。

（まとめ）

$$
\begin{align*}
\begin{cases}
\alpha+\beta=-\dfrac{b}{a} &\leftarrow（\boldsymbol{\small こちらは既知}）\\
\alpha-\beta=  \cdots  &\leftarrow（\boldsymbol{\small こちらが問題}）
\end{cases}
\end{align*}
$$

$${\cdots}$$ の部分は平方根を用いて  $${\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}}$$  と決定できたので

$$
\begin{align*}
\begin{cases}
\alpha+\beta=-\dfrac{b}{a}\\
\alpha-\beta=\pm\sqrt{{\left(\dfrac{b}{a}\right)}^2-4\cdot\dfrac{c}{a}}
\end{cases}
\end{align*}
$$

という連立方程式を解くことによって２次方程式の解 $${\alpha,  \beta}$$ が決定でき、それが解の公式そのものとなります」
「大変よくできました。平方根を取ることによって生じるプラスとマイナスの入れ替えが、$${\alpha}$$ と $${\beta}$$ の置換へとうまく対応していることも重要な事実だね。では森田君、３次方程式の場合はどうかな？」
「はい。３次方程式の場合も同じようなステップで説明できます。重解も含めて３次方程式には解が３つあるので、その３つの解を $${\alpha,  \beta,  \gamma}$$ としたときの解の差積
　$${X=(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)}$$
を最初に考え、この差積の２乗
　$${X^2=\{(\alpha-\beta)(\beta-\gamma)(\gamma-\alpha)\}^2}$$
が対称式となることを利用し、その平方根を取ります。差積の２乗の平方根を考えるところまでは２次方程式と同じですが、この後が違ってきます」
「そうだね、では森田君、少し休憩をいれようか。３次方程式の方は５分後に始めよう」
「わかりました」
　竹村は休憩を入れた。
「３次方程式は差積の平方根を取ることによって遇置換まで対称性を破壊し……」
　竹村は自分の予習ノートを見返した。

（了）

（コメント）
　３次方程式の場合は次の記事に回します。本シリーズは、３次方程式の場合と同じアイデアを５次方程式でやろうとすると矛盾が起き、よって５次以上の方程式に解の公式が存在しない、という流れになります。これは「アーベルの証明」（アーベル・ルフィニの定理）で、それを解説してから「群」という新しい概念を用いてより核心に迫った「ガロアの証明」へと続きます。
　ただ今後は図やグラフを多用したいので、図形やグラフが描けるようnote運営部にリクエストしてみようかと思います（図やグラフを描けないと他で作って画像として貼り付けることになるので、かなり面倒です）。座標に任意の数式のグラフが描けるようになればと思います。
　なるべく当時の素朴な知識だけで、現代数学の専門的なことは使わないで書いていきます。とはいえアーベルやガロアの原論文そのものだと、（当時の数学的な道具立てが未整理だったか？）日本語訳をみても非常に分かりにくいので、その急所のアイデアを忠実に守りながらも、高校数学だけで分かるように柔らかく書いていきます。

（参考）
　各テーマの内容
（１）「２次方程式の解の公式」を式変形で導出
　　　・平方完成
（２）「３次方程式の解の公式」を導出するための準備
　　　・$${1}$$ の３乗根 $${\omega}$$
（３）「３次方程式の解の公式」を式変形で導出
　　　・チルンハウス変換
（４）「解と係数の関係」と「対称式」の解説
（５）「対称式」を用いた「２次方程式の解の公式」の導出
（６）「解の置換」と「ラグランジュ・リゾルベント」の解説
（７）「ラグランジュ・リゾルベント」による「３次方程式の解の公式」の導出
（８）「遇置換」と「奇置換」の解説（ここから「アーベルの証明」の準備）
（９）「差積の２乗」が対称式となることを解説
（10）「平方根」「３乗根」と次々と累乗根を加えていくアイデア
（11）「アーベルの証明」のアイデアを用いて、なぜ「２次方程式の解の公式」が存在するのかを解説。