
生産者理論(1):生産集合
前回までは、価格理論のうち消費者理論を取り扱ったが、今回からは古典的な生産者理論を取り扱う。今回は、生産者(主に企業)を特徴づける生産集合の性質と生産ベクトルの解釈について整理する。連載はこちら。
経済学における企業の捉え方
伝統的なミクロ経済学(価格理論)では、企業が市場の中で果たす中心的な役割を明確に捉えるため、企業の内部は捨象し、生産要素を投入すると生産物を産み出すブラックボックスとして捉える。
一方、組織内部では制度や規則、慣習など価格メカニズムとは本質的に異なる力が働いており、こうした組織内部の分析にも近年脚光があたるようになった。一見すると資源配分が全て市場で決まっているように見えるが、実際は資源配分のかなりの部分が、企業組織の内部で、市場メカニズムとは異なったやり方でなされている。このことに気づいた経済学者のRonald Coaseは、1937年の「企業の本質」という論文で、次のような問題を提起した。
「なぜ資源配分のある部分は市場で行われ、また別の部分は企業内部の非市場的な活動を通じて行われるのか?」
換言すれば「企業と市場の境界線はどこで引かれるのか、ある企業と別の企業の境界線はどこで引かれるのか」という問題である。この問題はミクロ経済学の応用分野である組織の経済学が対象としている。以下ではその基礎付けとして、価格理論における生産者理論を取り扱う。
生産集合と生産ベクトル
$${N}$$次元実数空間$${\mathbb{R}^N}$$上での生産活動を描写するため、企業が技術的に可能な$${\mathbb{R}^N}$$上のベクトルの集合を生産集合$${Y}$$とする。一つの生産集合は、一つの企業を表すと考えられる。任意の生産集合$${Y \in \mathbb{R}^N}$$に属する$${y \subset Y}$$を$${N}$$次元の生産ベクトルという。但し、$${y}$$の要素のうち、産出要素を正の値、投入要素を負の値で表す。
生産ベクトル$${y}$$と生産集合$${Y}$$
$${y=(y_1, \cdots, y_k, \cdots, y_N)\in \mathbb{R}^N}$$
$${y_k≥0}$$:産出、$${y_k<0}$$:投入
$${Y\subset \mathbb{R}^N}$$
補足:生産ベクトルの解釈
$${N=2}$$の時、$${(-1, 1)\in Y, (-1, 2)\notin Y}$$であることは、第1財1単位を投入して第2財を1単位生産できるが2単位は生産できないことを表す。$${N=3}$$の時、$${(-1, -2, 3)\in Y, (-2, -1, 3)\in Y}$$とすると、第3財を3単位生産するときの費用最小化問題を考えることができる。
$${N=3}$$で$${(-1, 1, 1)\in Y}$$の時の解釈方法は様々ある。第1財1単位を使って第2財と第3財を1単位ずつ生産する結合生産とする考え方において、生産財の一つを人的資本とすればOJT的に解釈可能である。また、生産財の1つを公害などに解釈すると外部性を表現することができる。不確実性の存在する環境を考える場面で第2財と第3財がそれぞれ異なる状態の下で与えられる財を指すなら、第1財は各状態のどちらでも使える財と考えられる。
生産集合を考える時、投入物が利用可能かは問題とならない。例えば$${N=2}$$の時、$${(-100, 100)\in Y}$$は「もし100単位の第1財が投入されれば100単位の第2財を生産できる」ことを表しているにすぎず、必ずしも実際に100単位の第1財が生産に利用できることを意味しない。
生産集合の性質
生産集合$${Y}$$については以下のいくつかが仮定されることが多い。
生産集合$${Y}$$の性質
①非空性:$${Y≠\varnothing}$$
②閉性:$${Y}$$は$${\mathbb{R}^N}$$の閉部分集合である
③凸性:$${Y}$$は$${\mathbb{R}^N}$$の凸部分集合である
④フリーランチの不可能性:$${Y \cap \mathbb{R}_+^N \subseteq \{0\}}$$
⑤無生産の可能性:$${0\in Y}$$
⑥自由可処分:$${Y-\mathbb{R}_+^N \subseteq Y}$$
⑦不可逆性:$${Y \cap (-Y) \subseteq \{0\}}$$
⑧加法性:任意の$${\bar y \in Y}$$と$${\bar y' \in Y}$$について$${\bar y+\bar y' \in Y}$$
⑨規模に対する収穫非増加:
任意の$${\bar y\in Y}$$と任意の$${\alpha \in [0,1]}$$について$${\alpha y\in Y}$$
⑩規模に対する収穫非減少:
任意の$${\bar y\in Y}$$と任意の$${\alpha ≥1}$$について$${\alpha y\in Y}$$
⑪規模に対する収穫一定:
任意の$${\bar y\in Y}$$と任意の$${\alpha ≥0}$$について$${\alpha y\in Y}$$
④フリーランチの不可能性
フリーランチの不可能性は、生産集合$${Y}$$とゼロ以上の$${N}$$次元実数空間の積集合がゼロベクトルのみを含む集合の部分集合である、つまり生産要素を投入することなく生産物を生産することはできないという仮定である。
⑤無生産の可能性
生産集合$${Y}$$がゼロベクトルを要素として持つ場合、$${Y}$$は無生産の可能性を満たすと言う。これは、生産者が投入や産出を一切行わないことが可能であることを意味する。生産集合が原点を通らないとき、$${Y \cap \mathbb{R}_+^N = \phi}$$であり、空集合は任意の集合の部分集合のため、$${Y}$$はフリーランチの不可能性を満たすが、$${0\notin Y}$$すなわち無生産の可能性を満たさない。従ってフリーランチの不可能性を満たす生産集合は無生産の可能性を満たすとは限らない。
無生産の可能性は、短いスパンを分析するときには満たされないことが多い。土地や建物など長期賃貸契約、設備のリース契約などは、実際生産がおこなわれていなくても消費される投入要素だからである。無生産の可能性が満たされているということは、十分長い期間後、残存契約の無いゼロベースの状態から生産を始めることができることを言う。
⑥自由可処分
自由可処分は、生産者が制約なく生産物や生産要素を処分できるという仮定を表す。これは、生産集合$${Y}$$の境界(生産フロンティア$${Y^f}$$)が水平又は右下がりの時、$${Y^f}$$の下側が全て$${Y}$$に含まれることを表している。$${Y^f}$$に右上がりの部分がある時、$${Y}$$は自由可処分を満たさない。
⑦不可逆性
不可逆性とは、生産集合$${Y}$$と原点について対象となる集合$${-Y}$$の積集合がゼロベクトルのみを含む集合の部分集合である、つまり生産プロセスにおいて、投入要素と生産要素を丁度入れ替えた真逆のプロセスが成り立たないことを表している。
⑧加法性
加法性とは、2つの生産工程$${(y_1, y_2)}$$と$${(y_1', y_2')}$$を分けて行えば、生産者全体としては$${(y_1+y_1', y_2+y_2')}$$の生産計画を実施することができることを表す。投入物の利用可能性に制限がないという仮定の下では加法性は必ず満たされるが、もし工場立地などの問題により別々の生産ができないのであれば、それも投入量として考慮すべきである。
⑨⑩⑪規模に対する性質
規模に対する性質は、図形的には以下の対応関係にある(なお、上記の生産集合$${Y}$$はいずれも、フリーランチの不可能性、無生産の可能性、不可逆性、自由可処分も満たしている)。
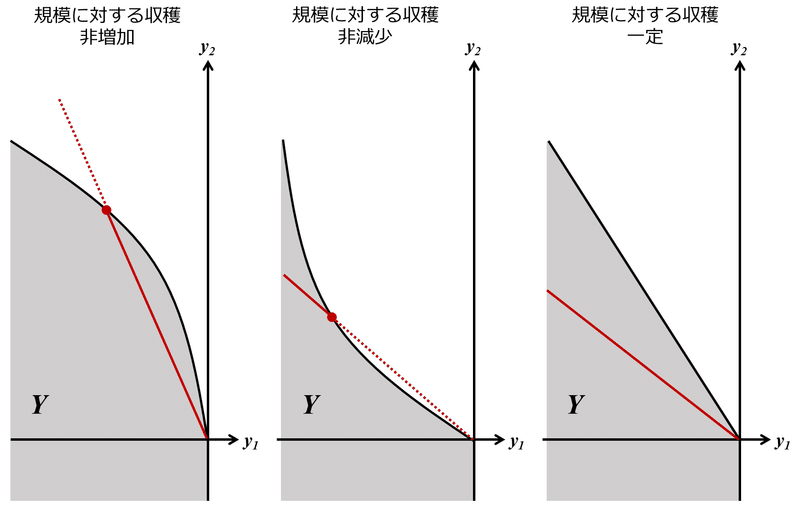
上図で例示していないが、境界がS字の生産集合は3性質のいずれも満たさない
収穫非減少は、利潤最大化の解を持たないが経済学的に重要なケースである。水光熱費などの固定費が莫大なインフラなど、規模の経済が働く業界で見られるケースだからである。このような問題は利潤最大化問題は解を持たなくとも、費用最小化問題を解くことができる。
収穫非増加は最も一般的に見られる性質である。収穫非減少と収穫非増加を同時に満たしているのが、収穫一定である。この場合、利潤は常にゼロとなり、経済学的に分析しやすいため、生産集合の最も妥当な定式化である。
***
最後に、$${Y}$$が凸集合であるとき、$${Y}$$は収穫非増加であり、生産要素平面上の等量曲線は原点に対し凸となる。この性質は、消費者理論における無差別曲線の議論と全く同様である。2点目の性質は、同じ等量曲線上の2点に対し、投入要素を組み合わせた方が好ましいことを意味している。
次回はこちら。
この記事が気に入ったらサポートをしてみませんか?
