前回に続き、ミクロ経済学において最も重要な帰結である「厚生経済学の基本定理」を学ぶ。今回は第二基本定理を取り扱い、任意のPareto効率的な配分を価格均衡により達成するための条件について議論する。連載はこちら。

証明の準備

弱Pareto効率性と価格準均衡

厚生経済学の第一基本定理の逆は成り立つだろうか。その疑問に答えるものが、厚生経済学の第二基本定理である。まず、この定理に現れる弱Pareto効率性、価格準均衡を定義する。これらはそれぞれPareto効率性、価格均衡よりも弱い概念であり技術的なものに過ぎない(後述の分離超平面定理を用いてシンプルに証明するための定義と見なせる)が、Walras均衡の存在問題にも現れる重要な概念である。

ここで、強Pareto効率性：$${(x_1^*, \cdots, x_I^*, y_1^*, \cdots, y_J^*)}$$に対して$${\forall i \in \{1, \cdots, I\}:x_i ≻ x_i^*}$$を満たす$${(x_1, \cdots, x_I, y_1, \cdots, y_J)}$$を定義すると、弱Pareto効率性とは「それを強Pareto改善するような実行可能配分が存在しないこと」と定義することができる。

条件①は利潤最大化を意味しているが、条件②は選好最大化を意味していない。条件②を選好準最大化と呼ぶと、これは選好最大化よりも弱い条件である。選好準最大化において選択される消費計画は「その所得未満の支出で得られる消費よりは選好されるような消費」であり「その所得と同額の消費の中では、選好を最大化する消費とは限らない」ということである。選好最大化は「その所得以下の支出で得られる消費の中で、それよりも高い効用を得られないような消費」である。選好最大化が満たされていれば選好準最大化は満たされるが、一般にその逆は成り立たない。選好準最大化では$${p\cdot x_i = p \cdot x_i^* \land x_i ≻_i x_i^*}$$を許容しているためである。従って価格均衡は価格準均衡でもあるが、その逆は一般には成り立たない。

価格準均衡と価格均衡は、任意の消費者$${i}$$が価格ベクトル$${p}$$の下で$${p \cdot x_i^*}$$未満の支出で「生きる」ことができれば、それらは同意である。もし$${p \cdot x_i^*}$$が「生きる」のに最低限必要な所得であるなら、効用準最大化の条件は必ず満たされる。厳密には、$${x_i^* \in X_i}$$が価格ベクトル$${p}$$の下で最小所得条件を満たす、つまり$${\exist x_i \subset X_i: p \cdot x_i < p \cdot x_i^*}$$となる時である。

また、厚生経済学の第二基本定理を証明するために次の定理を用いる。

分離超平面定理

Euclid空間$${\mathbb R^N}$$における超平面とは、非ゼロの法線ベクトル$${p \in \mathbb R^N \setminus \{0\}}$$とスカラー$${c \in \mathbb R}$$から$${H(p, c)=\{x \in \mathbb R^N | p\cdot x = c\}}$$と定義される$${\mathbb R^N}$$の部分集合である(上図のように、$${\mathbb R^2}$$における超平面は直線となる)。

集合$${X, Y}$$が互いに素であり、かつともに凸集合である場合に、これらの集合$${X, Y}$$を分離する超平面が必ず存在することを主張する定理が分離超平面定理である。この定理に現れる法線ベクトル$${p \in \mathbb R^N \setminus \{0\}}$$が理論価格に相当する。従って、選好の凸性と総産出可能性集合の凸性は、厚生経済学の第二基本定理の成立に本質的に重要と言える。

厚生経済学の第二基本定理

この定理は、任意のPareto効率的配分が達成可能であることを意味している。つまり、価格メカニズムがPareto効率性以外の他の制約や条件を均衡配分に課すことはない。更に、任意のPareto効率的配分が、分権的な価格メカニズムの作用によって達成可能であることを表す。すなわち、消費者には自身の選好最大化、企業には利潤最大化を追求させることで、Pareto効率的配分が達成可能となる、ということである。

但しそれには一括税や一括補助金が可能という条件が必要である。この定理で存在が保証されている$${p}$$によって所得配分$${(p\cdot x_1^*, \cdots, p\cdot x_I^*)}$$が決まっているため、このような配分が不可能であれば、定理は現実には適用できない。つまり、この富の再配分が可能であるときに限り定理は有用である。

選好の凸性は、消費の多様性を好むものと解釈できる。消費集合$${X}$$に属する2つの消費計画$${x, x' \in X}$$に対し、その凸結合$${\alpha x + (1-\alpha)x'     (\alpha \in [0,1])}$$は、両端の消費計画の間をとったものだが、それが両端の消費計画(のうち好ましくない方)と少なくとも同等以上に選好されるということは、ある特定の財だけを消費する極端な消費計画よりも、色々な財を消費する多様な消費を好むということである。動学的なモデルでは、特定の期に多く消費することよりも平準化された消費を好むことを意味する。

総産出可能性集合の凸性は、収穫逓増を排除する。総産出可能性集合$${\sum_j y_j}$$に$${0}$$が属する(無生産の仮定)なら、任意の生産計画$${y}$$に対し、$${\alpha y   (\alpha \in [0, 1])}$$は$${0}$$と$${y}$$との凸結合$${\alpha y + (1-\alpha)0}$$にほかならず、$${\sum_j y_j}$$が凸集合であればこれは$${\sum_j y_j}$$に属する。この条件は収穫逓減(非逓増)を意味する。

第二定理が総産出可能性集合の凸性を仮定する必要があるのは、収穫逓増産業がある経済では分権化は達成できないためであり、電気や水道などの収穫逓増産業への政府の介入はこのことにより正当化される。但し、$${\sum_j y_j}$$が凸集合であれば十分であり、個々の$${y_j}$$が凸集合でなくとも$${\sum_j y_j}$$が凸集合であることがあり得る(大数の凸化効果)ため、全ての$${j}$$について$${y_j}$$が凸集合であることは$${\sum_j y_j}$$が凸集合であることの十分条件であって必要条件ではない。加えて凸化効果が存在することを考慮すれば、$${\sum_j y_j}$$の凸性の仮定は強いものではないと考えられる。例えば以下の図のような同一の生産集合$${Y}$$を持つ多数の企業を考えると、それらの企業のうち、$${y}$$もしくは$${y'}$$だけ生産する企業の割合を任意に変化させることで、線分$${yy'}$$上の任意の生産を実現することができるようになる。消費集合$${X}$$の凸性と個々の消費者の選好の凸性の間にも同様の議論が成り立つ。凸化効果の議論は、以下のShapley-Folkmanの補題を参照。

定理の証明

配分$${(x_1^*, \cdots, x_I^*, y_1^*, \cdots, y_J^*)}$$をPareto効率的配分とし、以下の集合$${A_i, A, B}$$を定義する。

$${A_i = \{x_i \in X_i:x_i ≻_i x_i^*\},   A=\displaystyle\sum_{i=1}^I A_i,   B=\displaystyle\sum_{j=1}^J Y_j +\{\bar\omega\}}$$

選好$${≿_i}$$が完備性、推移性、凸性を満たす時、上方位集合$${A_i}$$は凸であるため(証明は消費者理論(3)を参照)、$${A}$$も凸集合である。また、仮定より$${\displaystyle\sum_j Y_j}$$は凸集合なので、$${B}$$も凸集合である。

次に、$${A \cap B = \varnothing}$$を背理法で示す。もし$${(x_1, \cdots, x_I) \in A \cap B}$$が存在すれば、ある$${(y_1, \cdots, y_J)\in Y_1 × \cdots × Y_J}$$が存在して$${(x_1, \cdots, x_I, y_1, \cdots, y_J)}$$は実行可能である。しかし$${(x_1, \cdots, x_I) \in A}$$より$${(x_1^*, \cdots, x_I^*, y_1^*, \cdots, y_J^*)}$$が弱Pareto効率的であることに矛盾する。従って$${A \cap B = \varnothing}$$が成り立つ。

分離超平面定理より、ある$${p \in \mathbb R^N \setminus \{0\}}$$とスカラー$${c \in \mathbb R}$$が存在し、$${\forall a \in A, b\in B: p\cdot b ≤ c ≤ p \cdot a}$$が成り立つ。

$${(x_1, \cdots, x_I) \in X_1 × \cdots ×X_I}$$とし、任意の$${i}$$について$${x_i ≿_i x_i^*}$$ならば、$${p \cdot \Bigg( \displaystyle\sum_{i=1}^I x_i \Bigg) ≥ c}$$が成り立つことを示す。局所非飽和性より$${\forall  k=1, 2, \cdots}$$に対して$${x_i^k ≻_i x_i \land x_i^k \rightarrow x_i  (n \rightarrow ∞)}$$となるような点列$${(x_i^k)_{n=1}^∞}$$が存在する。この時、推移性より任意の$${k =1,2 , \cdots}$$に対して$${x_i^k ≻_i x_i^*}$$が成立する。任意の$${k}$$について$${\displaystyle\sum_{i=1}^I x_i^k \in A}$$だから、分離超平面定理より、$${p \cdot \displaystyle\sum_{i=1}^I x_i^k ≥ c}$$が成り立つ。ここで、$${k → ∞}$$とすると$${p \cdot \Bigg( \displaystyle\sum_{i=1}^I x_i \Bigg) ≥ c}$$が成り立つ。特にこれは$${x_i=x_i^*}$$でも成立する。

一方、Pareto効率的配分は実行可能なので、$${x^*}$$における上記の逆向き不等式：$${p \cdot \Bigg( \displaystyle\sum_{i=1}^I x_i \Bigg) ≤ c}$$は$${\sum x_i^* \in B}$$により成り立つ。従って以下の等式

$${p \cdot \Bigg( \displaystyle\sum_{i=1}^I x_i^* \Bigg)=p \cdot \Bigg( \displaystyle\sum_{j=1}^J y_j^* +\bar\omega \Bigg)=c}$$

を得る。つまり、Pareto効率的配分において$${X}$$と$${Y}$$は接しており、両者は上式で表される超平面によって分離される。

最後に、$${(x_1^*, \cdots, x_I^*, y_1^*, \cdots, y_J^*)}$$とこの$${p}$$が価格準均衡を成すことを示す。それには、利潤最大化条件と選好準最大化条件を満たすことを確認すればよい。$${\forall  j,  y_j \in Y_j: y_j +\displaystyle\sum_{k ≠ j} y_k^*+\bar\omega \in B}$$より、分離超平面定理から

$${p \cdot \Bigg(y_j +\displaystyle\sum_{k ≠ j} y_k^*+\bar\omega \Bigg) ≤ c = p \cdot \Bigg( \displaystyle\sum_{k=1}^J y_k^* +\bar\omega \Bigg)}$$

が成立する。すなわち、$${p \cdot y_j ≤ p \cdot y_j^*}$$を得て、利潤最大化条件が示された。次に、任意の$${i}$$を固定し、$${\forall  x_i \in X_i : x_i ≻_i x_i^*}$$が成り立つとすると、分離超平面定理より

$${p \cdot \Bigg(x_i +\displaystyle\sum_{k ≠ j} x_k^* \Bigg) ≥ c = p \cdot \Bigg( \displaystyle\sum_{k=1}^I x_k^* \Bigg)}$$

が成り立つため、$${\forall  x_i \in X_i : x_i ≻_i x_i^* \Rightarrow p \cdot x_i ≥ p \cdot x_i^*}$$を得る。この対偶をとれば$${\forall  x_i \in X_i : p \cdot x_i^* > p \cdot x_i \Rightarrow x_i^* ≿_i x_i}$$も真であり、これは選好準最大化に他ならない。以上より、厚生経済学の第二基本定理が証明された。

集合の和と凸性の関係

ここまでの議論の通り、厚生経済学の第二基本定理にとって本質的に重要なのは消費集合と生産可能性集合の凸性であり、かつ仮に個々の主体の選好や生産可能性集合が非凸であったとしても集計された集合が凸であれば十分なのであった。以下では、集合の和と凸性の関係を表したShapley-Folkmanの補題について議論する。この補題は、多数の市場参加者が存在する大規模経済において、個々の主体の凸性を仮定せずとも凸化された経済をベースに均衡の議論を進める際に用いられる。この補題の理解に必要な以下の3つの概念を定義し、続いて補題の中身の議論に移る。

凸包、Minkowski和、Hausdorff距離

①凸包

凸包とは、 与えられた点をすべて包含する最小の凸多角形（凸多面体）のことである。2次元の集合における、元の図形とその凸包の具体例は以下の通りである(図形の出所はこちらであり、他に凸包の性質なども詳しい)。

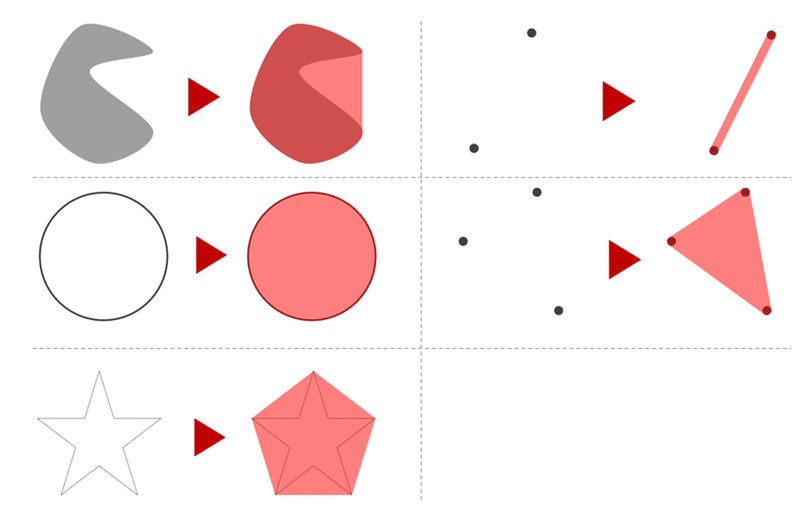
②Minkowski和

Minkowski和とは、図形(集合)の足し算を表す概念であり、例えば、$${0}$$と$${1}$$の2要素からなる集合$${\{0, 1\}}$$の、それ自身とのMinkowski和は以下の計算により$${\{0, 1,2 \}}$$となる。

$${\{0, 1\} +\{0,1\}= \{0+0, 0+1, 1+0, 1+1\}=\{0, 1, 2\}}$$

また、3つの正方形からなるL字ブロック同士のMinkowski和は、以下の図のようになる。

なお、Minkowski和については、以下の裃白沙氏のnoteに詳しい。

③Hausdorff距離

Hausdorff距離とは2つの集合の間の距離を表すものであり、直感的には「$${\forall a \in A}$$(もしくは$${\forall b \in B}$$)から$${B}$$($${A}$$)に到達するのに必要な最小距離」を意味する。つまり、$${A}$$に含まれる任意の点から$${B}$$までの最短距離のうちの最長距離を表す。以下の図の例では、$${A}$$に含まれる2点のうち、破線が$${B}$$に含まれる3点までの距離、赤い破線が$${A}$$の各点から$${B}$$までの最短距離、赤く太い破線がそのうちの最長距離、すなわちHausdorff距離である。

Hausdorff距離については、こちらのページに詳しい。

Shapley-Folkmanの補題

以下では上記の概念を前提に、Shapley-Folkmanの補題の直観的理解を試みる。$${\mathbb R^N}$$上の非空で有界な集合$${Q_1, \cdots, Q_I}$$、及びそれらのMinkowski和を$${Q=\displaystyle\sum_{i=1}^I Q_i}$$、凸包内の任意のベクトルを$${x \in \text{Cov}(Q)}$$とする。

まず「Minkowski和の凸包」は「凸包のMinkowski和」に等しい、すなわち$${\text{Conv}(Q)=\displaystyle\sum_{i=1}^I \text{Conv}(Q_i)}$$であるため、$${x \in \text{Cov}(Q)}$$に対して、$${x=\displaystyle\sum_{i=1}^I q_i}$$となるような$${q_i \in \text{Conv}(Q_i)}$$が存在する。つまり集合の和の凸包内のベクトル$${x}$$を、個別の集合の凸包内のベクトル$${q_i}$$の和として表現できる。以上を踏まえ、Shapley-Folkmanの補題は次のように記述される。

この定理は、全体の凸包が、高々$${N}$$個の個別集合の凸包と残りの個別集合それ自身との和で表現できることを主張している。考慮される集合の数$${I}$$を$${N}$$に対して十分大きくしていくと、近似的に全体の凸包が、ほぼ全ての個別集合それ自身の和で表現できることになる。いま、個別集合の凸性は何ら仮定していないため、上記を裏返せば「個別の集合の凸性を仮定せずとも、それらを十分大量に集めた時の集合の和は、近似的に凸性を満たす(凸包と見なせる)」ことを意味する。

上述の$${0}$$と$${1}$$の2要素からなる集合$${\{0, 1\}}$$とそれ自身とのMinkowski和：$${\{0, 1,2 \}}$$を考える。つまり、

$${N=1,  Q_1=Q_2=\{0, 1\}, \text{Conv}(Q_1)=\text{Conv}(Q_2)=[0,1], \\ Q=\{0, 1, 2\}, \text{Conv}(Q)=[0,2]}$$

である。ここで、$${[0, 2]=[0, 1]+[0, 1]=\text{Conv}(Q_1)+\text{Conv}(Q_2)}$$は、一つの集合($${Q_1}$$とする)の凸包である$${[0,1]}$$と他の集合$${Q_2=\{0, 1\}}$$の和で表せることが分かる。さらに$${Q_3=\{0,1\}}$$を追加すると$${x\in [0,3]}$$は$${q_1 \in [0,1], q_2, q_3\in\{0, 1\}}$$の和で表現可能となる。以下同様に$${Q_I}$$まで追加した場合には$${x \in [0,I]}$$は$${q_1 \in [0,1], \forall i \in \{2, \cdots, I\}:q_i\in \{0,1\}}$$の和で表現できる。ここで$${I \rightarrow \infin}$$において、$${x \in \text{Conv}(Q)}$$は近似的に$${q_i\in \{0,1\}}$$の総和で表せると見なせるため、非凸集合である$${\{0, 1\}}$$内のベクトルの集合で任意の実数$${\mathbb R}$$を表すことができる、言い換えれば無数の集合$${Q_i  (i=1, \cdots)}$$が数直線上を埋め尽くすようになる、と解釈できる。

ここで、上記の帰結をより直感的に理解するために、スケール影響を排除する。具体的にはMinkowski和に対し、集合の数で除した平均値を用いる。例えば$${I=2}$$では$${\dfrac{1}{2}Q=\bigg\{0, \dfrac{1}{2}, 1\bigg\}}$$である。この時、元の集合$${\{0, 1\}}$$の凸包$${[0, 1]}$$と$${\dfrac{1}{2}Q}$$とのHausdorff距離$${d_H \bigg([0,1], \dfrac{1}{2}Q\bigg)}$$を計算すると、以下のようになる。

$${d_H\bigg([0,1], \dfrac{1}{2}Q\bigg)=\bigg|\dfrac{1}{2}-\dfrac{1}{4}\bigg|=\bigg|0-\dfrac{1}{4}\bigg|=\bigg|1-\dfrac{3}{4}\bigg|=\bigg|\dfrac{1}{2}-\dfrac{3}{4}\bigg|=\dfrac{1}{4}}$$

ちなみに$${[0, 1]}$$と$${\{0, 1\}}$$では$${d_H([0,1], Q)=\dfrac{1}{2}}$$であるため、同じ集合2つのMinkowski和の平均をとることで、Hausdorff距離が小さくなった。同様に$${I=3}$$のケースでは$${\dfrac{1}{3}Q=\bigg\{0, \dfrac{1}{3}, \dfrac{2}{3},1\bigg\}}$$で$${d_H\bigg([0,1], \dfrac{1}{3}Q\bigg)=\dfrac{1}{6}}$$、一般の$${I}$$のケースでは$${\dfrac{1}{I}Q=\bigg\{0, \dfrac{1}{I}, \dfrac{2}{I},\cdots, \dfrac{I-1}{I}, 1\bigg\}}$$で$${d_H\bigg([0,1], \dfrac{1}{I}Q\bigg)=\dfrac{1}{2I}}$$、$${I \rightarrow \infin}$$で$${d_H\bigg([0,1], \dfrac{1}{I}Q\bigg)\rightarrow 0}$$、つまり集合$${\{0, 1\}}$$のMinkowski和の平均値は、集合の数が無数に存在するとき、元の集合の凸包$${[0, 1]}$$に等しくなることが分かる。

このことはShapley-Folkmanの補題の通り任意の非空で有界な集合で成り立つため、例えば視覚的にはL字ブロックにおけるMinkowski和の平均をとると、やがて元の集合の凸包に近づくことが見てとれるだろう。

この事実は、Gabriel Peyré氏のXによれば、以下のフランスの地図や像が凸包に帰着するようなイメージで表現されており興味深い。

余談だが、物理学者はしばしば過度に理想化された非現実的な仮定の下で理論を構築するが、その姿勢は「牛を球で近似する」などと揶揄される。一方、経済学の世界では、市場の参加者が有限だが十分多数存在する場合には非凸な選好を持つ消費者の集合であっても、総体として「球」つまり凸性を満たすものとして近似しても良い、と見なされる点は面白い。

※凸化に関する他の議論として、Aumannが連続濃度の経済主体からなる市場モデルを用いて「個々の消費者や生産者の市場影響力が無限小かつ参加者数は有限」という完全競争のジレンマを数学的に解決しつつ、個々の経済主体の効用の凸性を仮定せずとも連続無限和をとる社会全体の効用は凸性を満たすことを示した。この凸化効果はLyapunovの定理として知られ、連続経済主体や連続財集合などを含む市場モデルで重要な役割を果たす。

以上、厚生経済学の第二基本定理、及び大規模経済における凸性を広範囲に保証するShapley-Folkmanの補題を取り扱った。今回でミクロ経済学の核心となる厚生経済学の基本定理を区切りし、次回以降は私有経済や、ここまでその存在を前提として性質を論じてきた均衡の存在問題を取り扱う。