前回までは、個別の消費者や生産者の最適化行動を取り扱ってきた。今回は、消費者や生産者が複数存在する市場経済において、市場全体の需要関数や供給関数が、個別の需要関数や供給関数の総和として表現されるために満たすべき条件を明らかにし、均衡分析の準備を行う。連載はこちら。

生産者の集計

$${J}$$社の生産者が存在する生産セクターを考える。第$${j}$$番目の生産者は$${Y_j}$$で表され、各$${Y_j}$$に対し供給関数、利潤関数が定義できる。この生産セクター全体の生産集合は、以下のように表される。

各$${Y_j}$$と$${Y}$$において、供給関数を非空にする価格ベクトルの集合を$${P_j=\{p_j\in\mathbb R^N|y_j(p)\not= \empty \},  P=\{p\in\mathbb R^N|y(p)\not= \empty \}}$$とする時、以下が成立する。

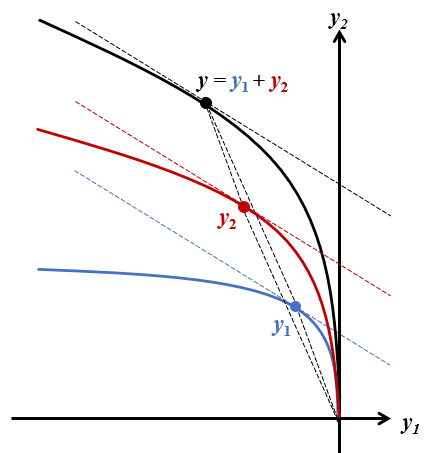
つまり、市場経済に$${J}$$社が存在する場合でも、生産集合$${Y}$$を持つ代表的生産者が1社存在すると見なして分析することができる。この生産集合において生産関数$${f(x)}$$は、次の問題の価値関数で定義される。

$${\displaystyle\max_{(z_1,\cdots,z_J)\in\mathbb R_+^J}\displaystyle\sum_{j}f_j(z_j)     \text{s.t.}  \displaystyle\sum_j z_j = z,  \forall j  z_j≥0}$$

なお、一般には$${f(z)\not=\displaystyle\sum_j f_j(z_j)}$$である。

この最適化問題におけるLagrangianは、次のように書ける。

$${L=\displaystyle\sum_{j}f_j(z_j)+\lambda_0\bigg(z-\displaystyle\sum_j z_j\bigg)+\displaystyle\sum_j\lambda_jz_j}$$

ここで、対称な生産関数系$${f_1=\cdots=f_J}$$という特殊なケースを考える。以下では、$${f(0)=0,  f_j>0, z>0}$$を仮定する。

①収穫逓減の場合
$${f_j}$$は凹関数で$${f_j''(z_j)<0}$$であり、1階条件が解の必要十分条件である。任意の$${j}$$に対し、最適解において$${f_j'(z_j)-\lambda_0+\lambda_j=0}$$が成り立つ。ここで$${\lambda_j>0}$$と仮定すると、相補性条件より$${z_j=0}$$。従って$${f_j'(0)=\lambda_0-\lambda_j<\lambda_0}$$となる。他方、$${z>0}$$よりある$${k}$$が存在し$${z_k>0}$$。この時相補性条件より$${\lambda_k=0}$$となり、$${f_k'(z_k)=\lambda_0}$$となる。いま、$${f_j=f_k}$$より$${z_k>0}$$かつ$${f_k'(0)< f_k'(z_k)}$$が成り立つが、これは$${f_k}$$が凹関数であることに矛盾する。従って任意の$${j}$$に対し$${\lambda_j=0}$$であり、$${f_j'(z_j)=\lambda_0}$$が成り立つ。

$${f_j'}$$は厳密な単調減少関数より、任意の$${j}$$に対し$${f_j'(z_j)=\lambda_0}$$が成り立つ$${z_j}$$は一意に定まる。従って$${z_1=\cdots=z_J=\dfrac{z}{J}}$$が解となり、$${f(z)=Jf_j\bigg(\dfrac{z}{J}\bigg)}$$が集計生産関数となる。

$${J\rightarrow ∞}$$の極限において、$${f_j\bigg(\dfrac{z}{J}\bigg)\approx f_j'(0)\Delta z=f_j'(0)\dfrac{z}{J}}$$に近似できるため、$${f(z)\approx Jf_j'(0)\dfrac{z}{J}=f_j'(0)z}$$、つまり限界生産性の最大値$${f_j'(0)}$$を傾きとする直線に近似でき、境界を含まない開集合となる。なお、ある$${z_0}$$が存在し$${z_j< z_0}$$の領域で収穫一定ならば、$${J\rightarrow ∞}$$の極限において各企業は$${z_j< z_0}$$の投入量で生産を行うため、集計生産集合は上記の直線を含む閉集合となる。

②収穫一定の場合
$${f_j}$$は$${f_j''(z_j)=0}$$を満たす。上記と同様に任意の$${j}$$に対し$${\lambda_j=0}$$であり、$${f_j''(z_j)=0}$$のため$${z_j}$$が任意の値で$${f_j'(z_j)=\lambda_0}$$となる。従って$${\displaystyle\sum_j z_j = z}$$を満たす任意の$${(z_1, \cdots, z_J)}$$が最適解となり$${f=f_j,  Y=Y_j}$$が成り立つ。

③収穫逓増の場合
$${f_j}$$は$${f_j''(z_j)>0}$$を満たす。この時関数の凸性より、任意の$${j}$$と任意の$${k\not= j}$$に対し$${z_j=z,  z_k=0}$$が解となり、$${f=f_j,  Y=Y_j}$$が成り立つ。

＊＊＊

上記の通り、$${Y}$$が拡張するケースは収穫逓減の場合のみである。企業数が大きくなるにつれ競争が激化し、生産量や価格が変化する可能性はあるが、生産技術は不変である。一方、非対称な生産集合の集計では、例えば収穫一定と収穫逓増の生産関数の組み合わせにおいて$${z}$$に応じ最大解が非連続的に変化するケースがあり得るなど、均衡分析に困難が生じる場合がある。

消費者の集計

次に、$${K}$$人の消費者が存在する市場経済を考え、消費者を集計することを考える。生産者$${j}$$が$${Y_j}$$で表されるように、消費者$${k}$$は$${(≿_k, I_k)}$$で表される。もし市場の総需要を個々の消費者の需要の総和

$${\displaystyle\sum_{k}x_k(p, I_k)=x\bigg(p, \displaystyle\sum_{k}I_k\bigg)}$$

として記述できれば、これを代表的消費者の需要関数と定義してもよさそうである。しかし一般にはこのような代表的消費者は存在しない。

Hicks需要を考える時には、消費者の集計は生産者の集計とほぼ同様である。効用水準$${\bar u_k}$$を固定したうえでHicks需要より消費者の需要を集計する場合、各消費者の上方位集合$${U_k=\{x\in X_k| u_k(x)≥\bar u_k\}}$$は生産者における生産者集合に対応する。生産集合の集計と同様に

$${U=\displaystyle\sum_{k}U_k=\bigg\{\displaystyle\sum_{k}x_k\in \cup_k X_k|  \forall k   u_k(x_k)≥\bar u_k\bigg\}}$$

で記述でき、個々の$${U_k}$$が凸集合ならば集計した$${U}$$も凸集合である。この場合、市場全体のHicks需要量は$${\displaystyle\sum_{k}\bar x_k(p, \bar u_k)}$$に一致する。

しかし、Walras需要ではこの議論が適用できない。目標効用水準$${\bar u_k}$$が変化すると$${U_k}$$が変わり、$${U}$$も変化する。この時、個々の$${\bar u_k}$$を変化させたときに無差別曲線が交わる可能性があり、代表的消費者を定義できなくなる。逆に、個々の$${\bar u_k}$$を変化させても無差別曲線が交わらないという強い仮定を選好関係に課すことで、代表的消費者を定義することができる。Walras需要$${x_k(p, I)}$$では価格体系$${p}$$を所与とする時、所得の変化により効用水準が変化するため、上記の仮定は「所得の変化によっては無差別曲線の形状が変わらない=需要関数が所得に依存しない(所得効果が無い)」という仮定を置くことに相当する。

以下の形を持つ間接効用関数をGorman型効用関数と呼び、上記の仮定を満たすことが知られる。いま、消費者$${k}$$の間接効用関数を以下で与える。

$${v_k(p, I_k)=a_k(p)+b(p)I_k}$$

所得の限界効用$${b(p)}$$が全ての消費者で同一かつ、その他の財に関する効用関数$${\alpha_i(p)}$$は消費者により異なる点が特徴である。Royの恒等式より、消費者$${i}$$の財$${n}$$に対する需要関数は以下で与えられる。

$${x_k^n(p, I_k)=-\dfrac{\dfrac{\partial v_k(p,I_k)}{\partial p_n}}{\dfrac{\partial v_k(p,I_k)}{\partial I_k}}=-\dfrac{\dfrac{\partial a_k(p)}{\partial p_n}+\dfrac{\partial b(p)}{\partial p_n}I_k}{b(p)}=\alpha_k^n(p)+\beta^nI_k}$$

但し、$${\alpha_k^n(p)=-\dfrac{\dfrac{\partial a_k(p)}{\partial p_n}}{b(p)},  \beta^n(p)=-\dfrac{\dfrac{\partial b(p)}{\partial p_n}}{b(p)}}$$

ここで、消費者$${k=1,\cdots,K}$$の財$${n}$$に対する需要を集計すれば、

となり、所得$${\displaystyle\sum_{k=1}^KI_k}$$を持つ代表的消費者の需要関数として、個々の消費者の需要関数と同型になる。この需要関数は以下の間接効用関数からRoyの恒等式を用いて導出できる。

間接効用関数がGorman型となる十分条件は、以下の2通りがよく知られる。

• 各々がホモセティック効用関数：$${v_k(p,I_k)=V(p)I_k}$$を持つ

• 各々が$${x^0}$$について準線形の効用関数：$${U_k(x_k^0, x_k^1,\cdots, x_k^N)=x_k^0+u_k(x_k^1,\cdots.x_k^N)}$$を持つ

準線形効用関数

準線形効用関数は、ある財$${x^0}$$について線形かつその他の財$${x^1,\cdots, x^N}$$について厳密に凹関数である効用関数と定義される。$${x^0}$$を価値基準財(Numéraire；ニュメレール)という。

以下では$${N=1}$$の場合で、準線形効用関数の基本的性質を議論する。この時、効用最大化問題は、以下のように定式化される。

$${\displaystyle\max_{x^0, x^1}  x_k^0+u_k(x_k^1)    \text{s.t.}   x_k^0+p^1x_k^1=I_k}$$

$${\Leftrightarrow \displaystyle\max_{x^1}  u_k(x_k^1)+I_k-p^1x_k^1}$$

となり、無制約の最大化問題に書き換えられる。内点解における1階、2階の条件として、以下を得る。

$${\dfrac{\partial}{\partial x^1}u_k(x_k^{1*})=u_k'(x_k^{1*})=p^1,   \dfrac{\partial^2}{\partial (x^1)^2}u_k(x_k^{1*})≤ 0}$$

従って1階条件から$${x_k^{1*}(p^1, I_k)=u_k'^{-1}(p^1)}$$が得られ、需要関数$${x_k^{1*}(p^1)}$$は所得に依存しない。つまり、所得効果(所得の変化に伴う財の需要量の変化)がゼロである。この時、間接効用関数は、以下の通り表せる。

また、限界代替率$${MRS_{10}}$$を計算すると、

$${MRS_{10}=\dfrac{\dfrac{\partial U_k(x_k^0, x_k^1)}{\partial x^1}}{\dfrac{\partial U_k(x_k^0, x_k^1)}{\partial x^0}}=\dfrac{\partial u_k(x_k^1)}{\partial x^1}}$$

となり、無差別曲線の傾きは$${x^0}$$の影響を受けない。図形的には以下の通り、最適解$${x_k^{1*}}$$は予算線を上方シフトさせても変化せず、従って$${x^1}$$は所得効果を受けない中立財と見なせる。

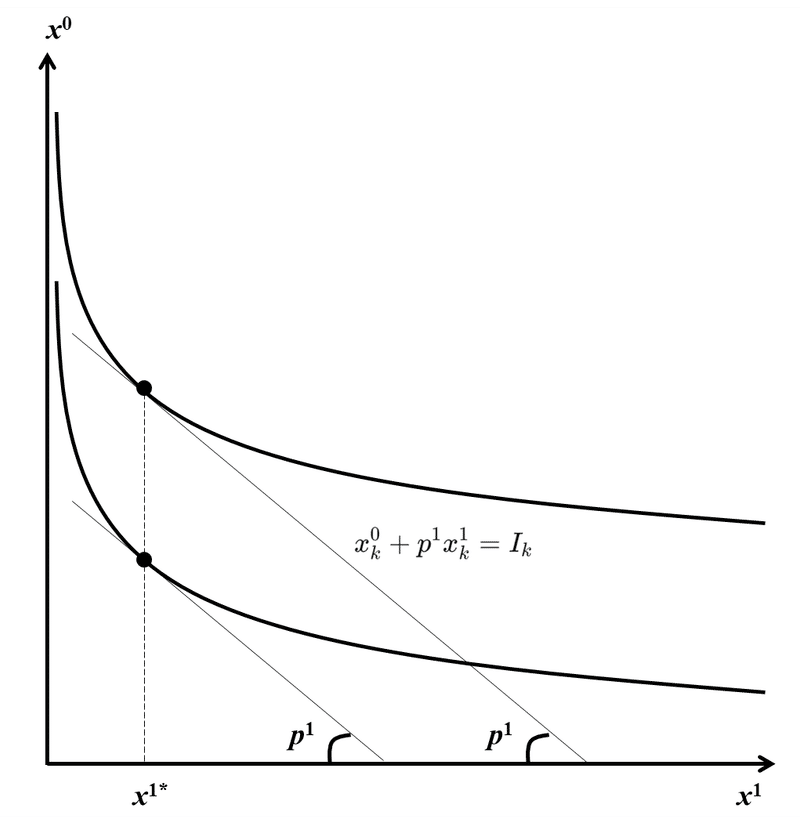
以上の議論をまとめると、消費者の選好として準線形効用関数を仮定することで、ニュメレール以外の財の所得効果がゼロとなり、間接効用関数がGorman型となるため、Royの恒等式により導出される需要関数を集計した代表的消費者の需要関数が個々の需要関数と同型となる。

価値基準財(Numéraire；ニュメレール)

準線形効用関数におけるニュメレール$${x^0}$$はしばしば「貨幣」と解釈される。準線形効用では貨幣の限界効用が一定値：$${\dfrac{\partial U(x^0, x^1)}{\partial x^0}=1}$$をとると仮定されており、財が貨幣と1種類の貨幣以外の財からなるとき、貨幣以外の財からなる個別需要関数において所得効果がゼロとなる特別な性質を持つ。

例えばニュメレールの価格を$${p^0}$$とする時、予算制約式は$${p^0x^0+p^1x^1=I}$$と書けるが、辺々を$${p^0}$$で除しても予算制約式の形状は変化しない。

$${x^0+\dfrac{p^1}{p^0}x^1=\dfrac{I}{p^0}}$$

そこで、$${x^0}$$の価格を基準とした相対価格$${\dfrac{p^1}{p^0}}$$と実質所得$${\dfrac{I}{p^0}}$$を改めて$${x^1}$$の価格$${p^1}$$と所得$${I}$$に設定し直す。つまり、予算制約式が0次同次であることから、貨幣という財の価格を1に基準化し、それと整合的な形で他の任意の財の価格と所得を相対的な形で表現しても何ら差し支えない。貨幣(を含む何らかの財)の価格を1へと基準化する時、その財をニュメレールと呼ぶ。

需要関数に関しても0次同次性が成り立つため、貨幣(を含む何らかの財)をニュメレールと定めてその価格を1へと基準化し、その他の全ての財の価格を表現しても、効用最大化問題の解は変化しない。需要関数の0次同次性は、貨幣単位の付け替えが経済学的には意味を持たないことを示唆している。

所得の単位が「円」である場合、価格ベクトルと所得の組$${(p, I)}$$のもとでの効用最大化問題の解集合を$${x^*(p, I)}$$とする。ここで、所得の単位を「銭」に変換すると先の価格ベクトルと所得の組は$${(100p, 100I)}$$と表現され、そこでの効用最大化問題の解集合は$${x^*(100p, 100I)}$$となる。需要関数が0次同次である場合には、$${x^*(100p, 100I)=x^*(p, I)}$$が成り立つため、所得の単位を「円」から「銭」に変更しても効用最大化問題の解は変化しない。通貨を「円」から「ドル」や「ユーロ」などに変更する場合にも同様の議論が成り立つ。つまり、需要対応が0次同次である場合には、貨幣の種類や単位を変更しても効用最大化問題の解は変化しない。

次回は、これらの集計された供給関数と需要関数を用いて均衡分析を行う。