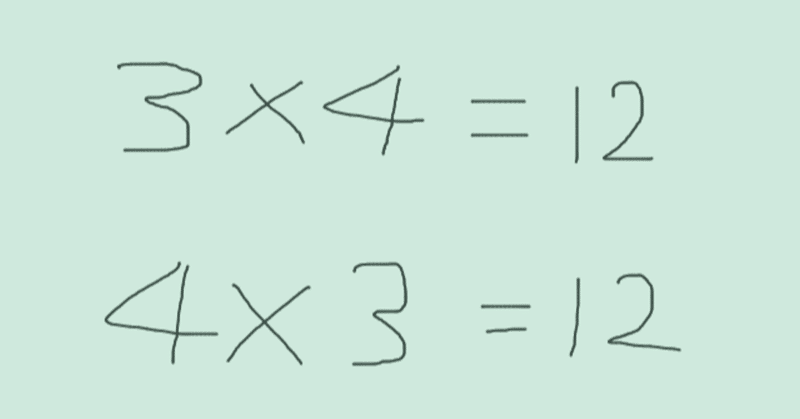
随筆(2021/1/26):小学校算数水準での数の掛け算の「順序」という、しばしば「数学」「教育」上有害にはたらく、公理っぽい何か(B.掛け算に並び方のある、例えば「行列」の話を、掛け算に並び方のない「数」にそのまま適用させることは有害である)
2_2_2_3.そもそも数の掛け算と関係ない場合
2_2_2_3_1.そもそも数の掛け算と関係ない場合
あと、これも混乱の元ですが、そもそも数の掛け算と関係ない話が、今回の数の掛け算の並べ方の話題にぶつけられることがあります。
今のうちに先取りして書くと、
「そういう話、何の益もなく、ただ混乱の元で害があるだけだから、やめといた方がいいのでは?」
ということになります。
(ここからやたら長い説明が続きます。
そもそも上の話に興味を感じない方は、今日の記事はすっ飛ばして結構です。
実りがあればよいので、出来れば読んで戴けると幸いですが…)
2_2_2_3_2.表みたいなのを扱う「行列」
例えば、かつて数学教育上大きな意味を持った、今でも数学上大きな意味のある、「行列」の話があります。
何らかの要素(数とは限らないことに注意)の列(数の列は特に「数列」と呼ぶが、必ずしも数の列に限らない)を組み合わせた、表みたいなものだと思って下さい。
列が2種類しかない場合が、表として一番イメージしやすいでしょう。もちろん3種類以上の組み合わせがあり得ます。
また、数列と行列が関係ある時とない時があり、これは場合場合に左右されます。一般的にはこれらに関係は特にありません。例えば、列の要素が{a,b,c,...}とかの変数でもいいし、変数の列の行列というのはもちろん可能です。
ちなみに、「集合」でなく、わざわざ「列」という場合は、「並べ方に意味があるものとして扱う」ことに注意して下さい。
重要な話として、今のカリキュラムでは、小中高で行列を習うことはなくなっています。
(だからかなり多くの人には、この記事自体が「何だっけこれ」というやつでしょう)
より重要な話ですが、行列は足し算や掛け算が出来ます。
さらに重要な話ですが、少なくとも小中高で習う範囲内では、全ての種類の数は、掛け算において、行列とは別種の振る舞いをします。だから、別種のものとして扱うべきです。
掛け算における、別種の振る舞い。それは何のことか。
ここが決定的に重要な話ですが、行列は、掛け算に「順序」があります。つまり、並び方に意味があります。
残念ながら、これが多くの生徒を混乱させて来た。
当たり前ですね。ふつうの数の掛け算とは丸っきり違う性質のものだからです。
(私も高校で文系を選択して、大学で新たに行列の講義を取って、大いに混乱した口です(そもそもなぜ大学で行列の講義なんか取ったんだお前?(気の迷いとしか…)))
まあ、文句の一つも出て来るでしょう。
「何でこんな、数とは違う掛け算のある、混乱の元のような数学的対象を、あえて勉強せねばならんのか?」
2_2_2_3_3.矢印みたいなのを扱う「線形代数学」
線形代数学という数学のジャンルがあります。
ベクトル空間とベクトルに関する分野です。
ベクトル空間とベクトルは、いわゆる「方向」や「矢印」を、一番基本的な形で表すものと言って、通常差し支えないでしょう。
(本当は違う。方向や矢印は、ベクトルを「見やすくしたもの」に過ぎない。ベクトルはもっと基礎的なものだ)
ベクトル空間とベクトルは、数学教育上だいぶ後でやる、隙間のない線のような数、実数全体を前提とします。
逆に、高校までのカリキュラムではおそらく最後に学ぶ、面のような数、複素数全体は、ベクトル空間とベクトルを前提とします。
(詳しくは説明しません。「そういうものだ。本当だった」ということがいつかわかる日が来るかもしれませんが、ここは説明を飛ばします)
方向のある矢印は、足し算が出来ます。
同じ方向の矢印同士を足したら二倍伸びますね。
逆の方向の矢印同士を足したら、それはどこにも伸びていない、出発点と同一視出来ます。
でも、違う方向の矢印同士の足し算は面倒です。どう計算するのか?
2_2_2_3_4.線形代数学の背景に行列が潜んでいる
実はここで、矢印の「足し算」をするために、暗黙裡に行列の「足し算」をやっているのです。
全ての(とりあえず2つの)列が、いわゆるxとyの2つの要素を持ち、それら要素は数であり、しかも列なので並び方に意味がある。と仮定します。例として、{x,y}={10,5},{-2,7}とします。
ふつうの平面を仮定しましょう。ふつうの平面を2次元ユークリッド空間と言います。説明しませんが、いわゆるベクトル空間に、様々な条件を加えたものになります。
上2つの列は、2次元ユークリッド空間上、「x=10,y=5である点」「x=-2,y=7である点」と同一視されます。
これらを原点({x,y}={0,0}であるような列と同一視してよい)と結ぶと、方向の違う斜めの線分が2本出来ます。
原点を出発点と見なすと、これは2本の矢印と同一視出来ます。
2次元ユークリッド空間上で、この2本の線分の足し算をすると、要するに「x=10+(-2)=8,y=5+7=12である点」と原点を結んだ線分になるのでした。
もちろんこれも新たな矢印と見なすことが出来ます。
ここで、同時に、行列の足し算をやってもいます。{x,y}={10+(-2)=8,5+7=12}ということです(ラフな書き方になっていますが、ご容赦下さい)。
行列の「足し算」は数の足し算と同じようなやり方なので、あまり悩むところはありません。
ということで、なんと、2つの数の要素を持つ2つの列(数列)による行列の足し算と、方向のある線分としての矢印の足し算が、直感的に納得の行く、一対一に対応するものとして扱えます。
これが、我々が直面する行列の、おそらく一番最初の例でしょう。
***
演算の機能がある以上、
「3つ以上の要素の足し算が出来るのではないか」
「足し算だけじゃなくて掛け算も出来るのではないか」
等の発展が期待出来ます。
そういう試みがあり、すると数とは異なる独特な性質があることが明らかになってきました。
それが例えば、
「行列の掛け算に関しては、順序対のように、並び方を考慮せねばならない」
というものです(詳しくは説明しません)。
これらの集大成が、複数の数列の演算を含む、線形代数学です。
複数の要素を持つ複数の数列の演算(これは行列の演算の一パターンでもある)の面倒さは、線形代数学を線形代数学たらしめる独特な性質の、重要な源の一つなのです。だったらしょうがない。
だが、じゃあ、その線形代数学とやらは、一体何の役に立つのか?
2_2_2_3_5.力は矢印の性質に逆らえない。正面からクリーンヒットするデカイ矢印が強い
線形代数学はいろいろな応用がありますが、一番暴力的な応用の説明をします。
物理学(特に運動の力である動力に関するふつうのニュートン力学)では、矢印の性質は前提です。
というか、運動は矢印の性質に露骨に従います。
じゃあ、線形代数学をやらないと、そのうち何も分からなくなります。
そういうメリットがあるので、線形代数学は大事なのです。
***
よく、俗っぽい言い方で、こういうのがあります。
「やはり暴力…暴力は全てを解決する…」
「何事も暴力で解決するのが一番だ」
***
しかし、その力は矢印の性質に逆らえません。
というか、力の解決能力は、実際には矢印の性質に起因しているところが大きい。
正面からクリーンヒットするデカイ矢印が強い。そういう話に絞ると、割とシンプルですね。
(なんという即物的な説明だ)
2_2_2_3_6.自然界の説明に有用だという意味でも、あの違和感のある行列の演算の勉強は、正当化しうる
もちろん行列と、その延長上にある、複数の要素の複数の数列の演算をやらないと、線形代数学はそのうち何も分からなくなる。
だからこそ、あの違和感のある行列の演算の勉強は、正当化しうるのです。
これを認めないと、自然界の力の振る舞いについて、いずれどんどん分からなくなっていく。
これは、困る。だから、行列の有用性を、認めざるを得ない。
2_2_2_3_7.(混乱の元の解体・乙)複素数の演算にベクトルの演算の性質は直接は反映されていないので、複素数の掛け算に並び方は関係ない
なお、「あれ?」となりますが、複素数の掛け算にも、並び方の都合はないのでした。
ベクトル空間や、(説明しませんが)その上位概念である2次元ユークリッド空間から、複素数全体を構成出来ます。
しかし、ベクトルの足し算と掛け算の並べ方の性質は、複素数の足し算と掛け算には、(説明しませんが)直接目に見えて反映はされていません。
純粋に数学の立場で言うと、自然数・整数・有理数・実数・複素数は、どれも掛け算に並べ方は関係ありません。
つまり、
「少なくとも小中高で、掛け算に並び方のある数を扱うことはない」
ということになります。
2_2_2_3_8.(混乱の元の解体・丙)掛け算に並び方のある「行列」の話を、掛け算に並び方のない「数」にそのまま適用させることは有害である
なので、掛け算に並び方のある「行列」の話を、掛け算に並び方のない「数」にそのまま適用させることは、何の益もない。
むしろ、混乱を招くだけであり、有害である。という話になります。
こうなると、小中高相手に「数」の演算について「行列」の話を引き合いに出す人は、
「小中高相手に数の計算についてアドバイスしている」
という目的意識がそもそもないのか?
だったらカテゴリーエラーである。そういう話、さっきも書いたが、何の益もなく、ただ混乱の元で害があるだけだ。やめときましょう。
2_2_2_3_9.(混乱の元の解体・丁)数学は仮定の約束事であり、便宜上有益な説明であり、説明時のメリットがデメリットより大きくないなら、採用する謂れがない
「害があるかどうかはどうでもいい。本当にそうかどうかが大事なんだ」?
「本当に」
の意味合いの話をしましょう。
かなり多くの場合、
「本当かどうか」
は
「物理的なモノと対応するか。そういうモノはあるか」
で分かります。
数学では、対応する物理的なモノの有無などどうでもいい。
だから、数学における
「本当かどうか」
とは、
「この文は、文として、おかしなところはないか」
とか、
「この文を作るために、行われた証明に、おかしなところはないか」
とか、
「この文は、特定の値(仮にこれを「真」と呼びます)と対応しているか」
とか、これらのいずれかの意味合いしかありません(しばしば最後の話を「真偽」として捉えることになります)。
かなりニュアンスが違いますね。
割り切ると、数学や論理や言葉一般は、ある種の説明であり、約束事です。
上のいろいろは、決めるのは自由だが、決めた後は従わねばならないような、何らかの性質を持つ何らかの約束事です。
上の「本当かどうか」のいろいろも、そういう約束事です。
繰り返しますが、物理的なモノの絡む実際の話は、数学にとっては関係のない話です。
(「その約束事の、さらなるルーツは、どういうものなのか?」
という話があります。
メチャクチャ面白いテーマですが、今回のテーマである数の掛け算の「順序」からかけ離れるから、やりません)
***
この話を何のためにしているかというと、こうです。
数の掛け算の「順序」や、行列の掛け算の「順序」は、そういう約束事であり、常に特定の値を取る絶対的真理ではない。
しかし、一旦ある約束事を仮定した、決めたら、それはその約束事の性質に従ってもらう。
で、ふつうは、その約束事を決めた「後」で、考えるべきことがある。
その約束事によって、さまざまな事柄の説明が出来るか。
そこで説明力や、あと文法や証明や値に問題はないか。
そういった観点から、そもそもどういう約束事を決めるかを、あらかじめ検討します。
そして。ここからが肝心ですが。
それらがダメだったら、その説明は放棄してよい。
役に立つなら使えばいいが、役に立たないのなら使ってられない。
数学は、対応する物理的なモノに、あるいは常に特定の値を取る真理に関係する何かではない。
そうではなくて、しばしば、物理的なモノを説明するための道具として使われる何かです。
道具としてダメなら、それは放棄して良い。こだわるべきところではない。
***
もうちょっと踏み込むと、数学にはいくつかの側面があります。
数学は、いくつかの仮定(公理)から、適正な手続き(推論規則)を踏んで作られる約束事としての、公理系によって成り立っています。
また、数学は、実在する何かの説明、例えば物理学にも使われる、広く一般的であるような、便宜上有益な説明でもあります。
この二つを合体させると、
「数学は実在する何かの説明たりうるが、それそのものは仮定の塊であり、数学的対象が物理的に実在しているという話は別にない」
という論点が出てきます。
非常にぎょっとするのですが、数学は仮定の約束事であり、有用性のある説明なのです。実在している保証はありません。
***
(倉田剛『現代存在論講義』I,IIで紹介されている、何人かの存在論系哲学者の説明があります。
そこでは、実在性とはしばしば量子より大きい中間サイズの物体の性質とほぼ同じであり、実在とは要するに物体とほぼ同じ意味合いになってしまっています。
この記事でも、「実在」という言葉を、物理的な意味合いを前提として使います)


というか、物理学が数学に基づいているのであって、数学が物理学に基づいているのではないんですよね。
数学は実在の前提に関わるものであり、逆ではない。
数学の実在を問う立場がありますが、そういう意味ではそもそもそれはカテゴリーエラーだと考えた方が良いのかも知れません。
(「じゃあこのカタカタ指で叩いて音がするキーボードは何だ。この指は何なんだ。
まさか数学的対象とは言うまいな。
そんなたわけた話にはついていけない」
というツッコミがもちろん考えられますが、これには
「いくつかの条件を満たした数学的対象は、何かの拍子で実在しうる、量子と同一視出来る。
実在と化した量子の集大成が、例えばキーボードや指である。
つまり、実在は、キーボードや指は、超高度な数学的対象である」
という即物的な説明が、実は可能です。
「もしもそれがアヒルのように歩き、アヒルのように鳴くのなら、それはアヒルに違いない」
という、いわゆるダック・テストの話です)
***
歴史的には、数学で広く受け入れられているような仮定(公理)と、その適正な手続き(推論規則)による結論のひとまとまり、様々な「公理系」は、メリットがデメリットを上回って大きいから広く受け入れられている。
デメリットがメリットと比べて、同じくらいであろうが、より大きくあろうが、比較不能であろうが。
とにかくデメリットが顕著に目立つ約束事、まあダメな約束事でしょう。
そういう約束事を、わざわざ受け入れる理由は、本来ないものです。
***
例えば、行列や行列の演算(掛け算含む)は有用性のある説明であり、ないと矢印(ベクトル)も力(運動の仕事をもたらす動力)も説明できない。
じゃあ、どんなに違和感があっても、その勉強を数学でやるのは、正当化されて何の不思議もない。
要するに、行列の掛け算の「順序」は、れっきとした有用性があり、それも考慮の上で、正当化される。
***
さて。
それでは、数の掛け算の「順序」には、そのような正当性は、果たして備わっているのだろうか?
(続きは、また次回)
応援下さいまして、誠に有難うございます! 皆様のご厚志・ご祝儀は、新しい記事や自作wikiや自作小説用のための、科学啓蒙書などの資料を購入する際に、大事に使わせて頂きます。
